【LeetCode每日一题】【2021/12/15】851. 喧闹和富有

851. 喧闹和富有

LeetCode: 851. 喧闹和富有

$中等$

有一组 n 个人作为实验对象，从 0 到 n - 1 编号，其中每个人都有不同数目的钱，以及不同程度的安静值（quietness）。为了方便起见，我们将编号为 x 的人简称为 "person x "。
给你一个数组 richer ，其中 richer[i] = [ai, bi] 表示 person ai 比 person bi 更有钱。另给你一个整数数组 quiet ，其中 quiet[i] 是 person i 的安静值。richer 中所给出的数据 逻辑自恰（也就是说，在 person x 比 person y 更有钱的同时，不会出现 person y 比 person x 更有钱的情况 ）。
现在，返回一个整数数组 answer 作为答案，其中 answer[x] = y 的前提是，在所有拥有的钱肯定不少于 person x 的人中，person y 是最安静的人（也就是安静值 quiet[y] 最小的人）。

示例 1：

输入：richer = [[1,0],[2,1],[3,1],[3,7],[4,3],[5,3],[6,3]], quiet = [3,2,5,4,6,1,7,0]
输出：[5,5,2,5,4,5,6,7]
解释： 
answer[0] = 5，
person 5 比 person 3 有更多的钱，person 3 比 person 1 有更多的钱，person 1 比 person 0 有更多的钱。
唯一较为安静（有较低的安静值 quiet[x]）的人是 person 7，
但是目前还不清楚他是否比 person 0 更有钱。
answer[7] = 7，
在所有拥有的钱肯定不少于 person 7 的人中（这可能包括 person 3，4，5，6 以及 7），
最安静（有较低安静值 quiet[x]）的人是 person 7。
其他的答案也可以用类似的推理来解释。

示例 2：

输入：richer = [], quiet = [0]
输出：[0]

提示：

• n == quiet.length
• 1 <= n <= 500
• 0 <= quiet[i] < n
• quiet 的所有值 互不相同
• 0 <= richer.length <= n * (n - 1) / 2
• 0 <= ai, bi < n
• ai != bi
• richer 中的所有数对 互不相同
• 对 richer 的观察在逻辑上是一致的

方法1：深度优先搜索

首先简单思考一下大致的流程：对于 ans[i]，找到富有程度不低于第 i 人的人（包括自己）视作数组，再找到数组中安静值最低的那个人。ans[i] 即为那个人的序号。

本题中的富有程度之间存在着间接的关系，比如给出 A 比 B 富有，B 比 C 富有，却不给出 A 比 C 富有，但它依旧是成立的。因此不好直接列出所有比 i 富有的人再比较安静值。所以我们可以使用有向图来表示。

如果 x 比 y 富有，则在 x 和 y 之间建立一条路径。由于我们要查找的是 比自己富有的人怎么怎么样，所以我们的路径要从 y 到 x，这样才能从 y 去访问比自己更富有的 x。

按示例1：richer = [[1,0],[2,1],[3,1],[3,7],[4,3],[5,3],[6,3]]，按照它构建出来的有向图如下：

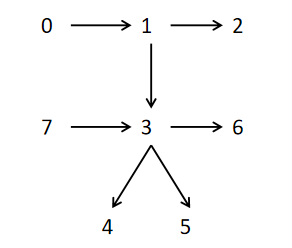
题目中提到 richer 中给出的数据 逻辑自恰（也就是说，在 person x 比 person y 更有钱的同时，不会出现 person y 比 person x 更有钱的情况 ），因此我们的有向图中可以保证 不出现环。

接下来就是存放图的信息了。我们可以使用哈希表，键为自身的序号 i，值为比自身富有的人的序号组成的数组。按照 示例1，最终的哈希表如下：

0: [1]
1: [2,3]
3: [4,5,6]
7: [3]

题目中提到人数为 n，而序号的范围为 0 至 n-1，因此我们可以不用 unordered_map ，而是直接申请一个长度 n 的动态数组，用序号去访问，尽管这样做可能空间消耗会大一点点。

前面说到用有向图去表示本题，但还没提到具体怎么操作。首先要考虑这个事情：在有向图的 终点，也就是那些 最富有 的人，比他们更富有的人不存在，因此安静值最小的也就是他们自己，ans[i]=i。也就是说，这些值是确定的答案。

而在研究那些 不是最富有的 人时，需要研究 比他们富有的人，到最后要 研究第二富有的人，最终会访问到 最富有 的人。也就是说，所有人的答案构成中，和 所有比自己富有 的人都有关系。这个过程的特点是从某人出发，从 最富有 的人往回递归，所以可以使用深度优先搜索来解决这个问题。

按照上文中按示例1构建的有向图：

则深度优先函数 dfs 中需要完成的事情有：

1. 由于题目要求是 富有程度不低于自己 的人去做安静值的比较，因此要把自己考虑在内，设 ans[x] 的初值为 x。
2. 根据哈希表，查出比 x 富有的人。
3. 对于这些人和自身，找出安静值最低的人，存入序号到 ans[x]。
4. 最终，dfs(0) 能够确定 ans[x]。

假设现在要求 0 的答案，即 ans[0]，我们对 0 调用深度优先搜索函数 dfs，dfs(0) 能确定 ans[0]。：

  dfs(0)
{ans[0]=0}

按照哈希表，hashtable[0]=[1]，也就是说 1 比 0 富有，能从 0 到达 1。所以要调用 dfs 去求 1 的 ans。

  dfs(0)    =>    [1]
{ans[0]=0}         |dfs(1){ans[1]=1}

然后，由于 hashtable[1]=[2,3]，因此 在求 ans[1] 之前要求 dfs(2) 和 dfs(3)。

  dfs(0)    =>    [1]
{ans[0]=0}         |dfs(1)    =>    [2,           3]{ans[1]=1}         |            |dfs(2)       dfs(3)    =>    [...]{ans[2]=2}   {ans[3]=3}

其中，由于 2 不能到达任何结点，因此 ans[2] 就被确定为 2。假设 ans[3] 算完了，现在，ans[2]和 ans[3]中存放的分别是 富有程度不低于2,3，对于2,3来说安静值最低的人的序号。

接下来递归的流程回到了 dfs(1)。dfs(1) 中，最终要确定 ans[1]，而确定 ans[1] 则要算 min{quiet[ans[1]]、quiet[ans[2]]、quiet[ans[3]]}，也就是自身，以及对于2和3的最安静的人这3个人之间，最安静的人。而这个人就是对于 1 来说最安静的人。

然后返回到 dfs(0) 同理，找到 0 和 ans[1] 这两个人之间最安静的人。

#include <vector>
#include <functional>
using namespace std;
class Solution
{
public:vector<int> loudAndRich(vector<vector<int>> &richer, vector<int> &quiet){const int n = quiet.size();vector<int> *hashtable = new vector<int>[n];for (const auto &kv : richer){hashtable[kv[1]].emplace_back(kv[0]);}vector<int> ans(n, -1);function<void(int)> dfs = [&ans, &hashtable, &quiet, &dfs](int x){if (ans[x] != -1)return;ans[x] = x;for (const int &y : hashtable[x]){dfs(y);if (quiet[ans[y]] < quiet[ans[x]]){ans[x] = ans[y];}}};for (int i = 0; i < n; i++){dfs(i);}return ans;}
};

代码中，对于lambda函数dfs定义时，不像往常写 auto，而是将它的类型直接写明：function<void(int)>。这是因为对于需要调用自身的lambda函数，其类型必须写明。

复杂度分析

• 时间复杂度：$O(n+m)$。其中，n 是数组 quiet 的长度，m 是数组 richer 的长度，建图和深度优先的时间复杂度均为$O(n+m)$。

• 空间复杂度：$O(n+m)$。需要 n 的空间来记录图中的点（哈希表的长度），m 的空间来记录图中的边（哈希表中所有值(数组)里的元素）。

参考结果

Accepted
86/86 cases passed (84 ms)
Your runtime beats 89.05 % of cpp submissions
Your memory usage beats 78.09 % of cpp submissions (41.4 MB)