Lorenz洛伦兹微分方程的Python求解

本文主要是介绍Lorenz洛伦兹微分方程的Python求解，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

本小节求解Lorenz微分方程：
在“数学之美”那一章里，为方便读者理解，Lorenz吸引子轨迹的计算采用了比较“原始”的方法。采用integrate模块中的odeint()函数可以更加方便地完成计算。Lorenz吸引子由下述三个微分方程定义：
$\frac{dx}{dt}=\sigma(y-x), \quad \frac{dy}{dt}=x(\rho-z)-y,\quad \frac{dz}{dt}=xy-\beta z$

版权声明

本文可以在互联网上自由转载，但必须：注明出处(作者：海洋饼干叔叔)并包含指向本页面的链接。

本文不可以以纸质出版为目的进行改编、摘抄。

本文节选自作者的《Python编程基础及应用》视频教程。

微实践 - Lorenz吸引子常微分方程组求解

在“数学之美”那一章里，为方便读者理解，Lorenz吸引子轨迹的计算采用了比较“原始”的方法。采用integrate模块中的odeint()函数可以更加方便地完成计算。Lorenz吸引子由下述三个微分方程定义：
$\frac{dx}{dt}=\sigma(y-x), \quad \frac{dy}{dt}=x(\rho-z)-y,\quad \frac{dz}{dt}=xy-\beta z$
其中，σ, ρ, β为参数。这些方程定义了三维空间中的一个无质量点(x,y,z)的各轴坐标相对于时间的速度矢量。我们这里需要计算随着时间t的变化，无质量点(x,y,z)的运动轨迹，也就是一组时间点上的系统状态。
在这里插入图片描述

源代码如下：

import numpy as np
from scipy import integrate
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3Ddef lorenz(p,t,s,r,b):x,y,z = p.tolist()          #无质量点的当前位置(x,y,z)print("x,y,z,t:",x,y,z,t)   #帮助理解odeint的执行过程return s*(y-x),x*(r-z)-y,x*y-b*z #返回dx/dt,dy/dt,dz/dtt = np.arange(0,30,0.01)
track1 = integrate.odeint(lorenz,(0.0,1.00,0.0),t,args=(10.0,28.0,2.6))
track2 = integrate.odeint(lorenz,(0.0,1.01,0.0),t,args=(10.0,28.0,2.6))
print("type(track1):",type(track1),"track1.shape:",track1.shape)fig = plt.figure(figsize=(12,6))
ax = fig.gca(projection='3d')   #获取当前子图，指定三维模式
ax.plot(track1[:,0],track1[:,1],track1[:,2],lw=1.0,color='r')	#画轨迹1			
ax.plot(track2[:,0],track2[:,1],track2[:,2],lw=1.0,color='g')	#画轨迹2			
...
plt.show()

控制台输出：

...
x,y,z,t: -5.64346434502397 -6.711791064199058 21.875348370569984 12.728116763457338
x,y,z,t: -5.6434643216721705 -6.7117909582448 21.875348207825766 12.728116763457338
x,y,z,t: -5.776218568580239 -7.038353710472807 21.677470196579595 12.739506857199522
...
type(track1): <class 'numpy.ndarray'> track1.shape: (3000, 3)

首先，定义了函数lorenz()，它的任分是计算无质量点坐标各方向相对于时间t的微分值。参数s,r,b分别对应方程组中的σ, ρ, β，t为时间（在函数里没有用到），p是一个ndarray，p.tolist()将其转换成一个列表，其中包括当前无质量点的坐标。

t = np.arange(0,30,0.01)以0.01有间隔，生成从0至30(不含)的等差数列，它代表了一组离散的时间点。

integrate.odeint()则进行微分方程求解，参数lorenz指明了微分计算函数，(0.0,1.00,0.0)则为无质量点的位置初始值；t为离散时间点；args指定了要传递给lorenz函数的额外参数，对应s,r,b，为固定值。odeint()会迭代调用lorenz()函数，用于生成无质量点的运动轨迹。上述控制台输出的结果可以帮助读者理解x,y,z坐标及t的变化过程。

t是一个长度为3000的一维数组，odeint()返回结果为一个形状为(3000,3)的二维数组，用3000个离散的三维空间点来表示无质量点的运动轨迹。据信，odeint()会将lorenz()函数返回的微分值再乘以dt以获得dx,dy和dz，这个过程其实跟我们在“数学之美”那一章的模拟计算过程类似，但更高效，更精确。

track1[:,0]对track1二维数组进行下标切片，得到3000个元素的一维数组，表示3000个空间点的x坐标，y和z坐标以类似方式获得。

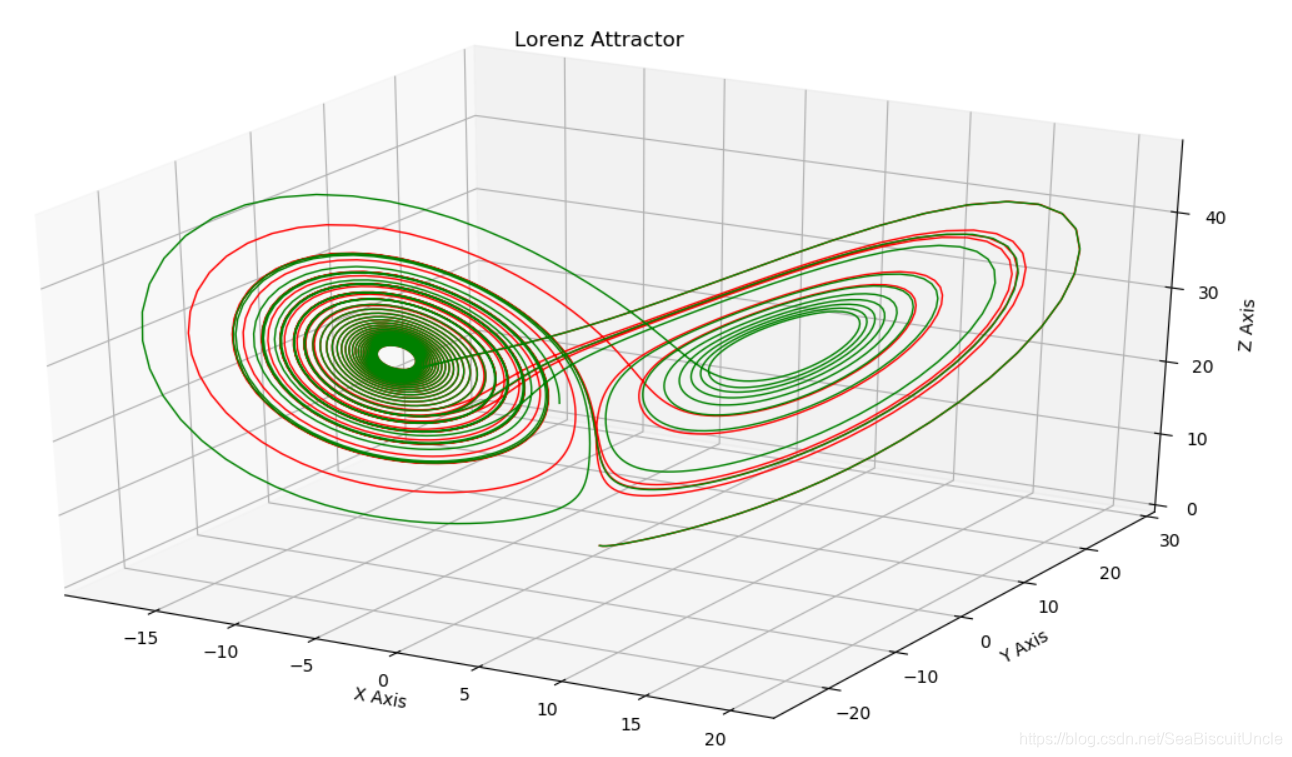
我们可以看到，track1-红和track2-绿仅在系统初始值上有细微差异，但随着时间的推进，其运动轨迹差异越来越大，表现出“混沌”性：南美洲一只蝴蝶扇动翅膀，会引起对面半球一场飓风。

本文节选自作者的《Python编程基础及应用》视频教程及同名教科书。想完整零基础学习Python程序设计，欢迎使用此免费视频教程。

在这里插入图片描述