求极限问题：x趋于0时的等价替换及其适用条件、洛必达法

本文主要是介绍求极限问题：x趋于0时的等价替换及其适用条件、洛必达法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

---

---

---

x趋于0时的等价替换及其适用条件

---

等价无穷小的定义：
若 $\lim \frac{\beta }{\alpha }=1$，则 $\beta$ 与 $\alpha$ 是等价无穷小的，记作 $\alpha \sim \beta$. 即当两个函数相比取极限，如果极限值为1，则这两个函数是等价无穷小的。

常用的等价替换（x趋于0时）

• $\sin x\sim x$

• $\arcsin x\sim x$

• $\tan x\sim x$

• $\arctan x\sim x$

• $e^x-1\sim x$

• $\ln (1+x)\sim x$

• $a^x-1\sim x\ln a,(a>0,a\ne 1.)$

• ${\log }_a(1+x)\sim \frac{x}{\ln a},(a>0,a\ne 1.)$

• $1-\cos x\sim \frac{1}{2}{x}^2$

• $(1+x{)}^{\alpha }-1\sim \alpha x$

• $(1+\beta x{)}^{\alpha }-1\sim \alpha \beta x$

• $\sqrt[n]{1+x}-1\sim \frac{1}{n}x$

• $x-\sin x\sim \frac{1}{6}{x}^3$

• $\arcsin x-x\sim \frac{1}{6}{x}^3$

• $\tan x-x\sim \frac{1}{3}{x}^3$

• $x-\arctan x\sim \frac{1}{3}{x}^3$

• $x-\ln (1+x)\sim \frac{1}{2}{x}^2$

---

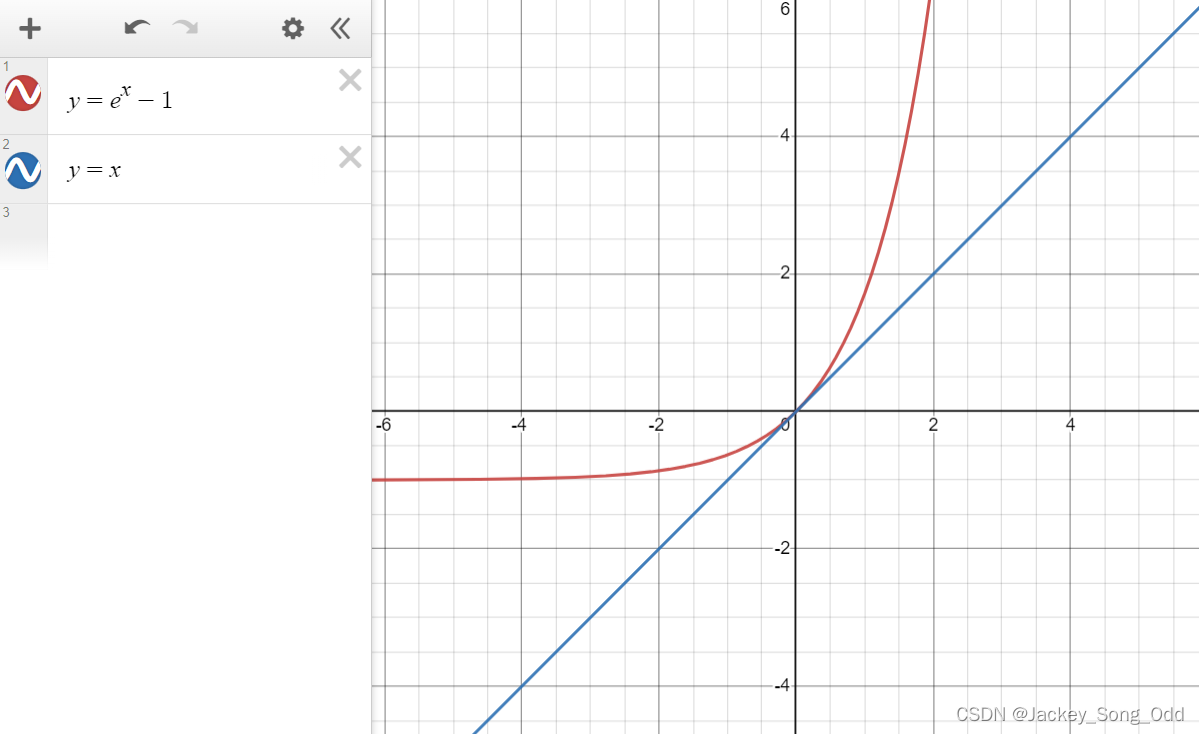
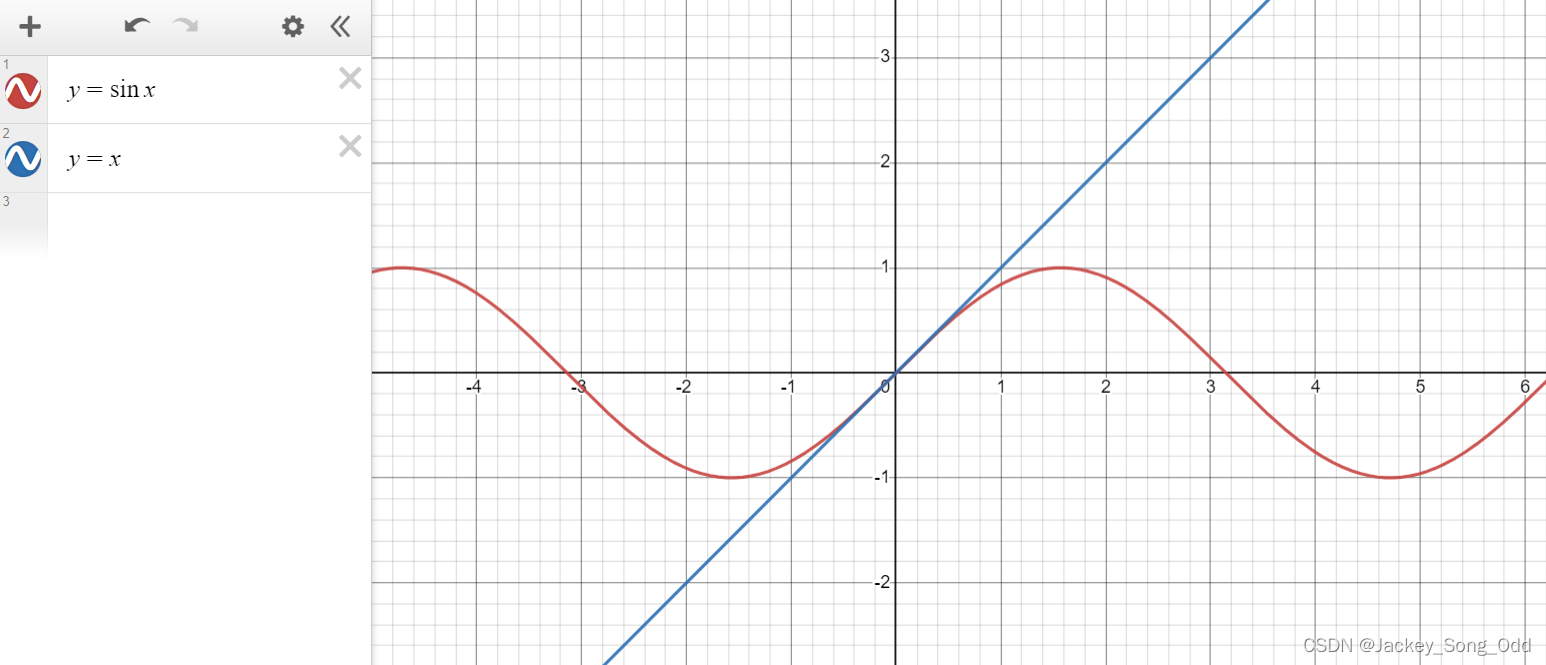
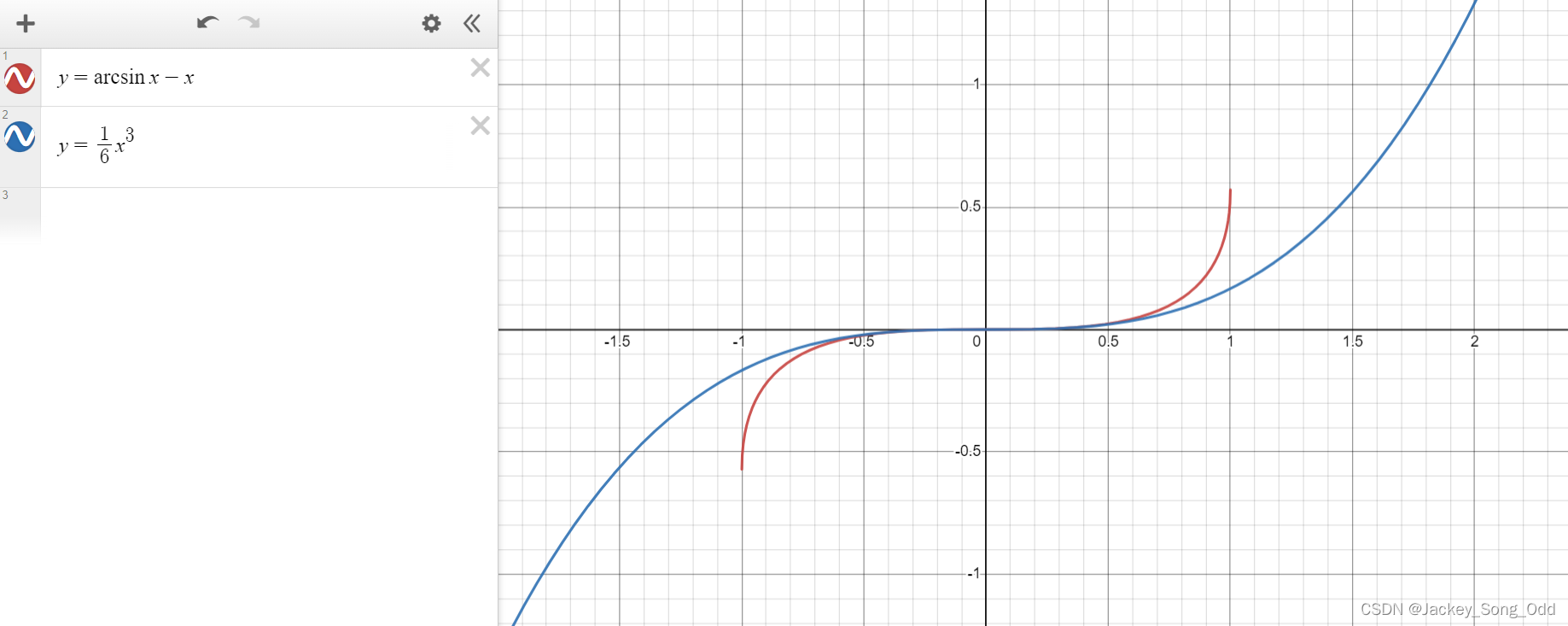
• 等价替换的本质是当x趋于某一点时，两个函数在该点处相切，即两函数在该点处斜率相同且只有该点处一个交点。 斜率相同，意味着两函数在该点处具有相同的增长率，在x的值无尽逼近于该点时，两函数值几乎相同，所以在求极限的时候可以用等价替换，来简化问题。从斜率（函数变化率）的角度也更容易理解洛必达法则。

---

洛必达法则：设
(1) 当 $x\to a$ 时，函数 $f(x)$ 及 $F(x)$ 都趋于 0；
(2) 在点 $a$ 的某去心领域内，$f^{\prime }(x)$ 及 $F^{\prime }(x)$ 都存在且 $F^{\prime }(x)\ne 0$；

(3) $\underset{x\to a}{\lim }\frac{f^{\prime }(x)}{F^{\prime }(x)}$ 存在（或为 $\infty$）

则 $\underset{x\to a}{\lim }\frac{f(x)}{F(x)}=\underset{x\to a}{\lim }\frac{f^{\prime }(x)}{F^{\prime }(x)}$.

洛必达法则使用于以下类型的极限中：(未定式类型)

• $\frac{0}{0}$

• $\frac{\infty }{\infty }$

• $0\cdot \infty$

• $0^0$

• $1^{\infty }$

• ${\infty }^0$

• $\infty -\infty$.

---

等价替换适用的条件

在求极限问题中，不是所有的情况都是可以直接用等价替换的。

从等价无穷小的定义中 $\lim \frac{\beta }{\alpha }=1$ 可以看出，$\alpha$ 与 $\beta$ 的极限比值为1，所以在乘除关系中，可以使用等价无穷小进行替换。

等价替换适用于乘除关系中，部分加减关系中可以用等价无穷小替换。大致如下：

• 若 $\alpha \sim {\alpha }_1$，$\beta \sim {\beta }_1$，则 $\lim \frac{\alpha }{\beta }=\lim \frac{{\alpha }_1}{\beta }=\lim \frac{\alpha }{{\beta }_1}=\lim \frac{{\alpha }_1}{{\beta }_1}.$

• 若 $\alpha \sim {\alpha }_1$，$\beta \sim {\beta }_1$，且 $\lim \frac{{\alpha }_1}{{\beta }_1}=A\ne 1$，则 $\alpha -\beta \sim {\alpha }_1-{\beta }_1$.

• 若 $\alpha \sim {\alpha }_1$，$\beta \sim {\beta }_1$，且 $\lim \frac{{\alpha }_1}{{\beta }_1}=A\ne -1$，则 $\alpha +\beta \sim {\alpha }_1+{\beta }_1$.

简单地讲就是，若极限的分子分母中有加减关系，且等价替换后加减关系的结果为0，这时候一般不能用等价替换。

这篇关于求极限问题：x趋于0时的等价替换及其适用条件、洛必达法的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---