锥规划问题存储格式——CBF格式简介

锥规划问题存储格式——CBF格式简介

前言

CBF(Conic Benchmark Format)，这是一种文件存储格式，整合了混合整数变量在混合圆锥（包括线性锥、二阶锥、半定锥、指数锥和幂锥）上的优化问题实例。该格式在设计时考虑了锥规划问题的基准库，因此侧重于紧凑且易于解析的表示。

1 问题形式

要使用CBF储存格式，首先要将凸优化问题化为CBLIB中使用的原始问题的标准参考形式：
$$\begin{array}{rl}\underset{x,X}{\mathrm{minimize}}& c^{T}x+⟨C,X⟩\\ \text{ subject to }& Ax+\mathcal{F}(X)-b\in {\mathcal{K}}_g^{n_g},\\ & {\mathcal{H}}^{\ast }(x)-B\in {\mathcal{S}}_{+}^{n_G},\\ & x\in {\mathcal{K}}_x^{n_x},X\in {\mathcal{S}}_{+}^{n_X},\text{ and }{x}_j\in \mathbb{Z}\text{ for }j\in \mathcal{I},\end{array}$$
其中$\mathcal{F}(X)$和${\mathcal{H}}^{\ast }(x)$定义如下：
$$\mathcal{F}(X)=\left[\begin{array}{c}⟨F_1,X⟩\\ ⋮\\ ⟨F_{n_g},X⟩\end{array}\right],{\mathcal{H}}^{\ast }(x)=\sum _{j=1}^{n_x}{x}_j{H}_j$$
$C\in {\mathcal{S}}^{n_X},B\in {\mathcal{S}}^{n_G},F_i\in {\mathcal{S}}^{n_X}$ for $i=$ $1,\dots ,n_g$, and $H_j\in {\mathcal{S}}^{n_G}$ for $j=1,\dots ,n_x$.

Note:

1. 上面的记号与大多数锥规划文献中所用记号类似，故不在此赘述

2 CBF文件结构

CBF文件由一系列信息块列表组成，而每个信息块的结构如下：

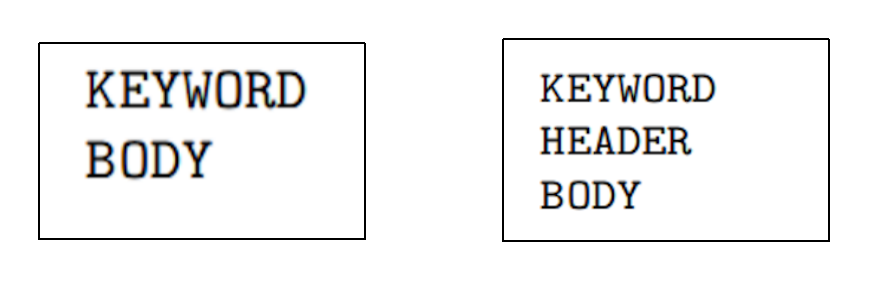
1. 第一行信息块是关键字，显示所提供信息的类型；
2. 第二行(某些关键字包含)是HEADER，说明变量的大小等信息，从而使求解器能够预先分配数据结构；
3. 其余的行是保存实际信息的BODY。

CBF文件主要由以下四类信息块构成：

3 实例

考虑如下凸优化问题，有半定锥约束，二次锥在无序子指标上的约束以及两个等式约束。

注意到，这并不是直接CBLIB中的标准参考形式，所以需要进行相应的转换。

1. 等式约束可以很容易重写为锥形式的约束 （ g 0 ， g 1 ） ∈ { 0 } 2 （g_0， g_1） \in \{0\}^2 （g0​，g1​）∈{0}2，方法是移动常量使右侧变为零;

2. $x_1\ge \sqrt{x_0^2+x_2^2}$表示$(x_1,x_0,x_2)\in Q^3$，而我们需要的是$(x_0,x_1,x_2)$，所以这里用一个仿射变换：
   $$\left[\begin{array}{lll}0& 1& 0\\ 1& 0& 0\\ 0& 0& 1\end{array}\right]\left(\begin{array}{l}{x}_0\\ x_1\\ x_2\end{array}\right)=\left(\begin{array}{l}{x}_1\\ x_0\\ x_2\end{array}\right)\in {\mathbf{Q}}^3$$

通过上面两步转换，可以得到该问题CBF格式：

Note:

1. PSDVAR
   • 1 : 表示只有一个属于半定锥的变量
   • 3：表示这个矩阵变量是$3\times 3$的
2. VAR
   • 3 1： 表示有三个标量变量属于1个锥
   • F 3：表示这个锥是F ，3维的

Note:

1. CON

   • 5 2：表示有5个约束，这五个约束属于两个锥
   • L= 2：表示第一个锥是L=，2维的（前两个约束属于这个锥）
   • Q 3：表示第二锥是Q，3维的（后三个约束属于Q这个锥）

2. OBJFCOORD

   • 5 ：表示目标函数中F矩阵有五个非零元

   • 第1列说明是第几个F矩阵

   • 第2、3列说明非零元在矩阵中的位置

   • 第4列给出非零元的值

3. OBJACOORD

   1. 1：表示标量变量只有一个系数非零
   2. 1 1.0：表示$x_1$的系数为1.0

4. CBF格式只存非零系数

5. 对称矩阵只存下三角

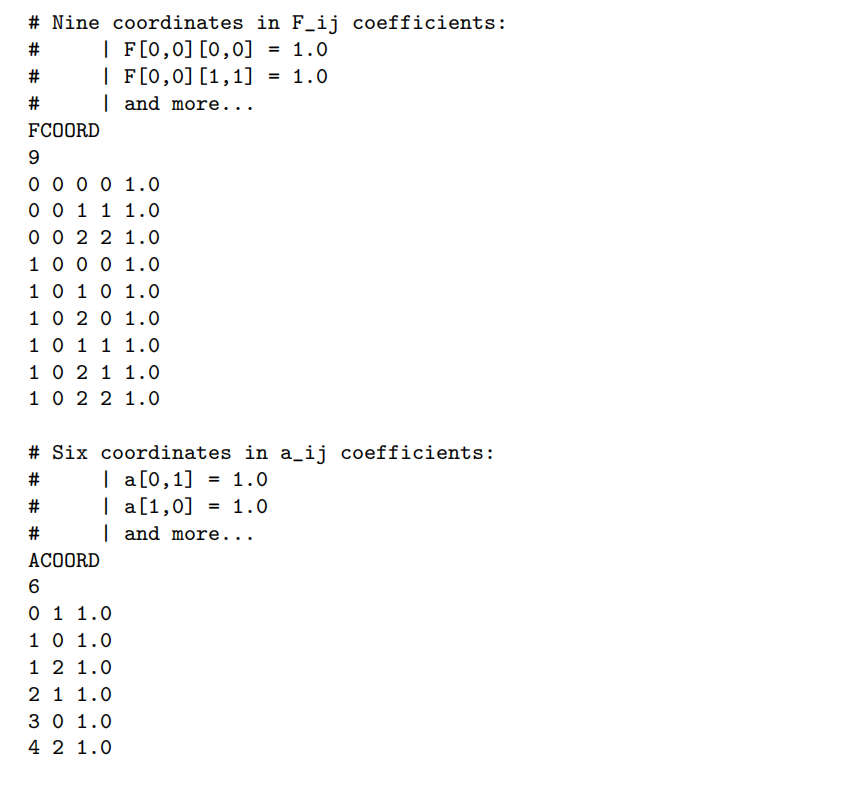
Note:

1. FCOORD
   • 9：表示约束中的F矩阵有9个非零元
   • 第1、2列：说明F矩阵的位置
   • 第3、4列：每个F矩阵中非零元的位置
   • 第5列：非零元的值
2. ACOORD
   • 6：表示约束中A矩阵有6个非零元
   • 其余表示类似
3. BCOORD
   1. 2：表示约束中b向量有2个非零元

参考文献

1. CBF-format4
2. CBLIB:2014