本文主要是介绍最大子段和问题(暴力 分治 动规),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
算法设计与分析--求最大子段和问题
问题描述:
给定由n个整数组成的序列(a1,a2, …,an),求该序列形如
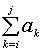
的子段和的最大值,当所有整数均为负整数时,其最大子段和为0。
1 暴力
int maxSum(int a[],int n)
{int maxSum = 0;int sum = 0;for(int i = 0; i < n; i++) //从第一个数开始算起{for(int j = i + 1; j < n; j++)//从i的第二个数开始算起{sum = a[i];a[i] += a[j];if(a[i] > sum){sum = a[i]; //每一趟的最大值}}if(sum > maxSum){maxSum = sum;}}return maxSum;
} 从最大子段和问题的解的结构可以看出,它适合用分治法求解。
a[1:n]的最大子段和有三种情形:
(1) a[1:n]的最大子段和与a[1:n/2]的最大子段和相同。
(2) a[1:n]的最大子段和与a[n/2+1:n]的最大子段和相同。
(3) a[1:n]的最大子段和为 ,
且1≤i≤n/2, n/2+1≤j≤n。
其中(1)和(2)这两种情形可递归求得。
对于情形(3), a[n/2]与a[n/2+1]在最优子序列中,a[1:n]的最大子段和是a[1:n/2]的最大子段和与a[n/2+1:n]的最大子段和的和。
int maxSum(int a[],int left, int right)
{int sum = 0;if(left == right) //如果序列长度为1,直接求解{if(a[left] > 0) sum = a[left];else sum = 0;}else {int center = (left + right) / 2; //划分int leftsum = maxSum(a,left,center); //对应情况1,递归求解int rightsum = maxSum(a, center + 1, right);//对应情况2, 递归求解int s1 = 0;int lefts = 0;for(int i = center; i >= left; i--) //求解s1{lefts += a[i];if(lefts > s1) s1 = lefts; //左边最大值放在s1}int s2 = 0; int rights = 0;for(int j = center + 1; j <= right; j++)//求解s2{rights += a[j];if(rights > s2) s2 =rights;}sum = s1 + s2; //计算第3钟情况的最大子段和if(sum < leftsum) sum = leftsum; //合并,在sum、leftsum、rightsum中取最大值if(sum < rightsum) sum = rightsum;}return sum;
}
3. 最大子段和问题的动态规划算法
这个算法可以通过动态规划分解为两步:
1,计算辅助数组。
2,计算辅助数组的最大值。
辅助数组b[j]用来记录一j为尾的子段和集合中的最大子断和。
例如,假如有一序列:-2,11,-4,13,-5,-2
则
b(1) = -2 ,b(2) = 11, b(3) = 7, b(4) = 20, b(5) = 15, b(6) = 13
a(1) = -2, a(2) = 11, a(3) = 7, a(4) = 13, a(5) = -5, a(6) = -2
b(1) < 0 b(2) > 0 b(3) > 0 b(4) > 0 b(5) > 0 b(6) > 0
---->
{ b(j - 1) + a(j) 当b(j-1) >= 0
b(j) = {
{a(j) 当b(j-1) < 0
for(i=1;i<=n;i++){scanf("%d",&a[i]);}int b=0;for(i=1;i<=n;i++){if(b<0)b=a[i];elseb=b+a[i];if(b>sum)sum=b;}
for(i=0;i<n;i++){scanf("%d",&a[i]);}int b=0;for(i=0;i<n;i++){b+=a[i];if(b<0)b=0;if(b>sum)sum=b;}
这篇关于最大子段和问题(暴力 分治 动规)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








