本文主要是介绍LeetCode22-黑白方格画,简易解题方法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
使用数学方法,进行分类讨论,得到最终结果。
先贴代码:
public class Solution1 {public static int paintingPlan(int n, int k) {int result = 0;//三种情况此种情况为1if(k==0||(k==1&&n==1)||n*n==k){result = 1;}else{int x = 0;//横排数量int temp = k;//黑色格子总值临时值if(k>=n){while(temp>0){x++;temp = temp - n;if(temp<=0){break;}else if(temp%(n-x)==0){//取余满足条件result += cFunction(n, temp/(n-x))*cFunction(n, x);}}//横排即可满足条件if(k%n==0){result += cFunction(n, k/n)*2;}}}return result;}//排列组合C的计算方式public static int cFunction(int n, int m){//代表C(n,m)return jc(n)/jc(m)/jc(n-m);}//阶乘方法public static int jc(int a){int result = 1;for(int i=a;i>0;i--){result *= i;}return result;}public static void main(String[] args) {int result = paintingPlan(3,8);System.out.println(result);}
}解题思路:
在此以10×10为例,如图所示
x x x x x x x x x x
x x x x x x x x x x
x x x x x x x x x x
x x x x x x x x x x
x x x x x x x x x x
x x x x x x x x x x
x x x x x x x x x x
x x x x x x x x x x
x x x x x x x x x x
x x x x x x x x x x
①k为0则无黑格,结果为1
②k为1-9不满足条件,结果为0
③k为10代表一行或者一列满足条件,即C(10,1)*2
④k为11-18不满足条件,结果为0
⑤k为19代表一行和一列的组合,此时结果为C(10,1)*C(10,1)
...
⑥k为100,即所有涂黑,结果为1
至此所有的情况列举完毕。
再举一个k为60的情况,即为6个整行,或6个整列,或2整行5列,或5整行2列
解题方法,行列是对称的结果,以行先涂,列后涂
定义一个临时值temp初始赋值为k,不停的减n,同时记录x代表涂了几行。有两种情况,要么k为n的倍数,即③情况,要么不满足k为n的倍数,即⑤情况,后续代码两种情况需要区分。
对于⑤情况,即k减去n后的剩余值,是否为n-x的倍数,满足条件整除即可得到y(涂了几列),使用排列组合C(n,x)*C(n,y)即可
例子解析,可结合代码理解:
k为19,temp初始为19,第一次减去10,x记录为1,剩余值为9,9为n-x[10-1]的倍数,满足条件,y为9/(10-1)为1,结果为C(10,1)*C(10,1)
k为60为例子,temp初始化为60,第一次减去10,x记录为1,剩余50除以9除不尽。第二次减去10,剩余40除以8满足条件,y为40/8=5,x为2,使用排列组合得到结果C(10,2)*C(10,5),进行累加。第三次减去10,剩余30除以7除不尽。第四次减去10,剩余20除以6除不尽。第五次减去10,剩余10除以5满足条件,y为10/5=2,x为5,使用排列组合得到结果C(10,5)*C(10,2),进行累加。第六次减去10,剩余0,y为0,x为6,这种情况比较特殊,需要特殊处理,即C(10,6)*2。
代码解析:
第一种判断:if(k==0||(k==1&&n==1)||n*n==k)
①k=0代表无黑格,即不画,所以为1
②k和n都为1,即1×1的格子全部画黑,为1种情况
③n和k相等,即全部画黑,为1种情况
x为横排数量,temp为临时值,初始化等于k,对于k<n的为不满足条件的,例如n=10,k=8这种。
进行while循环,不停的减去n,同时累加x得到行数,进行取余得到y值,满足条件进行累加。
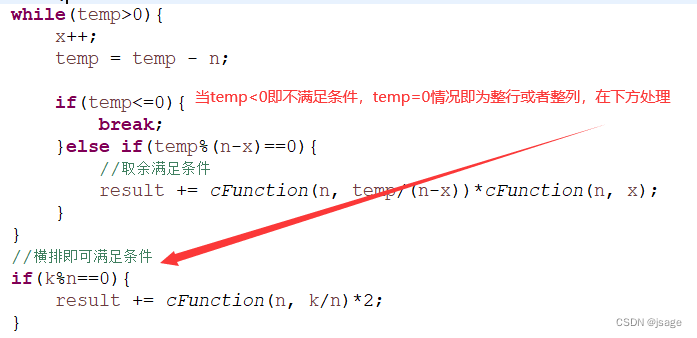
代码也可修改为temp<0。

执行结果:

这篇关于LeetCode22-黑白方格画,简易解题方法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



