本文主要是介绍python马踏棋盘,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
问题描述
现在有一个国际象棋棋盘(为8×8的方格棋盘)。现将棋子“马”放在棋盘上的任意位置,按照“马”走棋的规则(L形路线)将“马”进行移动。要求每个位置只能进入一次,最后要让棋子“马”走遍棋盘上的64个位置。请编写一个Python程序,完成上述操作,并用1~64这64个数字标注“马”移动的路径,也就是按照求出的行走路线,将数字1~64依次填入棋盘的方格中,并打印到屏幕上。
此问题的本质就是:利用递归思维不断的去尝试下一个落子的位置,除了最后一个落子位置以外,其余的每个落子位置至少存在1个可移动位置,至多存在8个可移动位置。所以这是一个最大递归深度为64,但递归广度非常大的问题。我们在1~8中取一个中间值4,假设每次落子的位置都有4个可移动位置,那我们将需要尝试落子的次数为4的64次方。340282366920938463463374607431768211456是一个很大的数字,即使用我们的电脑去尝试落子这么多次也要花很久的时间。所以这里我们不用去找出所有的落子路线,只找到一条就可以了,找多了影响我们电脑的使用寿命。(计算速率很大的电脑当我没说)
计算可移动位置
国际象棋中马走的是一个L形路线,假设第一次落子的位置在(5, 5),那它会有如下图中8个白色的可移动位置。

所以我们可以得出一个结论,当落子位置在(x,y)时,可移动位置有(x - 2, y + 1)、(x - 1, y + 2)、(x + 1, y + 2)、(x + 2, y + 1)、(x + 2, y - 1)、(x + 1, y - 2)、(x - 1, y - 2)、(x - 2, y - 1)。然而不是所有的可移动位置都在棋盘内,例如落子位置为(1,1)时,可移动位置只有(2,3)和(3,2)两个,其他的位置都在棋盘外了。所以我们在找出可移动位置后还需要判断该位置是否在棋盘内。
我们根据上述过程设计出一个计算可移动位置的函数,来帮我们计算出当前落子位置的可移动位置有哪些。根据马走L形路线的规则,我们可以设计出如下代码:
def return_location(x: int, y: int):"""返回可移动位置有那些:param x: x坐标:param y: y坐标:return: 可移动位置列表"""l_list = [] # 创建一个列表来存储可移动位置if x - 2 > 0 and y + 1 < 9: # 判断此位置是否超出棋盘l_list.append((x - 2, y + 1)) # 没有超出棋盘,则放入列表中if x - 1 > 0 and y + 2 < 9:l_list.append((x - 1, y + 2))if x + 1 < 9 and y + 2 < 9:l_list.append((x + 1, y + 2))if x + 2 < 9 and y + 1 < 9:l_list.append((x + 2, y + 1))if x + 2 < 9 and y - 1 > 0:l_list.append((x + 2, y - 1))if x + 1 < 9 and y - 2 > 0:l_list.append((x + 1, y - 2))if x - 1 > 0 and y - 2 > 0:l_list.append((x - 1, y - 2))if x - 2 > 0 and y - 1 > 0:l_list.append((x - 2, y - 1))return l_list # 返回可移动位置列表递归找位置
递归找位置的方法类似于一个二叉树,从根节点开始一个分支一个分支的去找。如下图所示:
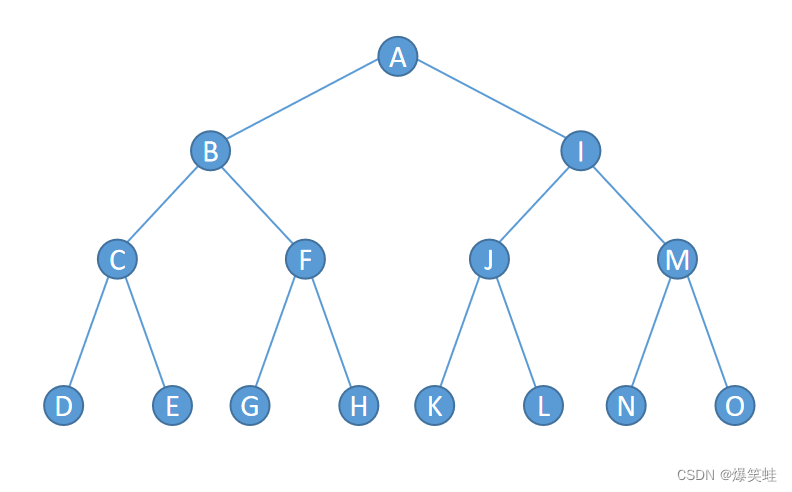
从第一个位置A开始,有两个可移动位置B和I。选择移动到位置B,有两个可移动位置C和F。选择移动到位置C,有两个可移动位置D和E。选择移动到位置D,如果位置D不满足要求,就从位置D返回C,再从位置C选择另一个位置E。如果位置E也不满足要求,说明位置C下面的分支都不满足要求,直接从位置C返回到位置B。再从位置B移动到位置F,尝试F下面的所有位置是否满足要求。如果F下面的位置都不满足要求,说明位置B下面的分支都不满足要求,直接返回位置A。再从A移动到I,查看I下面的各个分支,直到满足要求为止。上面这个二叉树只有3层深度,每个位置的可移动位置只有2个,马踏棋盘的深度为64,每个位置的可移动位置最少1个最多8个,会形成非常多的分支。虽然分支数量不同,但查找方式却相似。
通过递归不断的去寻找下一个可移动位置是否存在,我们可以得到很多条递归线路。但不一定所有的递归线路都可以达到64的深度,我们只需要递归找到一个递归深度为64的线路就可以结束程序了。我们为了记录递归线路和判断出可移动位置是否重复移动,要使用一个公共列表来存储移动过的位置。遇到移动过的位置就不再向此位置移动。代码如下:
def full_chess_board(x: int, y: int):"""使用递归找出能填满整个棋盘的线路:param x: x坐标:param y: y坐标:return: bool,当递归深度为64时返回True,否则返回False"""chess_list.append((x, y)) # 把落子位置放入公共列表中if len(chess_list) == 64: # 判断棋盘所有位置是否都已落子(递归深度是否为64)return True # 返回Truefor i in return_location(x, y): # 使用循环把可移动位置逐个输出if i not in chess_list: # 判断该位置在列表chess_list中是否存在if full_chess_board(i[0], i[1]): # 使用递归判断向下一个可移动位置移动是否可行(不断递归下去,能否达到64的深度)return True # 返回Truechess_list.remove((x, y)) # 此位置所有的分支都为绝路时,把此位置从公共列表中移除return False # 返回False在棋盘中打印落子顺序
通过调用full_chess_board函数来递归查找出每次落子的位置,在对应的位置上标注出落子序号(1~64),打印出这些序号在棋盘中所对应的位置。我们可以设计出如下函数:
def print_chess_order(x: int, y: int):"""在棋盘中打印落子顺序:param x: x坐标:param y: y坐标:return:"""if type(x) != int or type(y) != int: # 判断x和y的类型是不是intraise TypeError('x, y type must int') # 不是int则抛出类型错误if x < 1 or x > 8 or y < 1 or y > 8: # 判断x和y的值是否在[1, 8]范围内raise ValueError('x, y range [1, 8]') # 超出范围抛出值错误full_chess_board(x, y) # 执行递归查找填充路线print(chess_list) # 打印出棋子行走坐标row_list = [[0] * 9 for i in range(9)] # 创建一个二维列表来存放行走顺序(1~64)number = 1 # 第一个落子位置序号为1for i in chess_list: # 通过循环来逐个输出落子位置row_list[i[0]][i[1]] = number # 在棋盘对应位置记录落子序号number += 1 # 循环一次序号加一print('-' * 41) # 打印棋盘上边缘线for i in range(1, 9): # 通过循环逐个输出1到8的数字for j in range(1, 9): # 通过循环逐个输出1到8的数字print(f'|{row_list[i][j]:^4}', end='') # 取出二维列表中棋盘对应位置的序号,并打印出来print('|') # 棋盘右边界线print('-' * 41) # 打印棋盘底部边界线完整代码
我们可以在递归函数中加一个公共变量来查看递归函数被调用的次数,代码如下:
chess_list = [] # 存放落子位置的公共列表
times = 0 # 记录递归函数被调用次数的公共变量def return_location(x: int, y: int):"""返回可移动位置有那些:param x: x坐标:param y: y坐标:return: 可移动位置列表"""l_list = [] # 创建一个列表来存储可移动位置if x - 2 > 0 and y + 1 < 9: # 判断此位置是否超出棋盘l_list.append((x - 2, y + 1)) # 没有超出棋盘,则放入列表中if x - 1 > 0 and y + 2 < 9:l_list.append((x - 1, y + 2))if x + 1 < 9 and y + 2 < 9:l_list.append((x + 1, y + 2))if x + 2 < 9 and y + 1 < 9:l_list.append((x + 2, y + 1))if x + 2 < 9 and y - 1 > 0:l_list.append((x + 2, y - 1))if x + 1 < 9 and y - 2 > 0:l_list.append((x + 1, y - 2))if x - 1 > 0 and y - 2 > 0:l_list.append((x - 1, y - 2))if x - 2 > 0 and y - 1 > 0:l_list.append((x - 2, y - 1))return l_list # 返回可移动位置列表def full_chess_board(x: int, y: int):"""使用递归找出能填满整个棋盘的线路:param x: x坐标:param y: y坐标:return: bool,当递归深度为64时返回True,否则返回False"""global times # 声明公共变量times += 1 # 每调用一次递归函数times加一chess_list.append((x, y)) # 把落子位置放入公共列表中if len(chess_list) == 64: # 判断棋盘所有位置是否都已落子(递归深度是否为64)return True # 返回Truefor i in return_location(x, y): # 使用循环把可移动位置逐个输出if i not in chess_list: # 判断该位置在列表chess_list中是否存在if full_chess_board(i[0], i[1]): # 使用递归判断向下一个可移动位置移动是否可行(不断递归下去,能否达到64的深度)return True # 返回Truechess_list.remove((x, y)) # 此位置所有的分支都为绝路时,把此位置从公共列表中移除return False # 返回Falsedef print_chess_order(x: int, y: int):"""在棋盘中打印落子顺序:param x: x坐标:param y: y坐标:return:"""if type(x) != int or type(y) != int: # 判断x和y的类型是不是intraise TypeError('x, y type must int') # 不是int则抛出类型错误if x < 1 or x > 8 or y < 1 or y > 8: # 判断x和y的值是否在[1, 8]范围内raise ValueError('x, y range [1, 8]') # 超出范围抛出值错误full_chess_board(x, y) # 执行递归查找填充路线print(chess_list) # 打印出棋子行走坐标print(times) # 打印出使用递归函数的次数row_list = [[0] * 9 for i in range(9)] # 创建一个二维列表来存放行走顺序(1~64)number = 1 # 第一个落子位置序号为1for i in chess_list: # 通过循环来逐个输出落子位置row_list[i[0]][i[1]] = number # 在棋盘对应位置记录落子序号number += 1 # 循环一次序号加一print('-' * 41) # 打印棋盘上边缘线for i in range(1, 9): # 通过循环逐个输出1到8的数字for j in range(1, 9): # 通过循环逐个输出1到8的数字print(f'|{row_list[i][j]:^4}', end='') # 取出二维列表中棋盘对应位置的序号,并打印出来print('|') # 棋盘右边界线print('-' * 41) # 打印棋盘底部边界线print_chess_order(1, 1)运行结果如下:
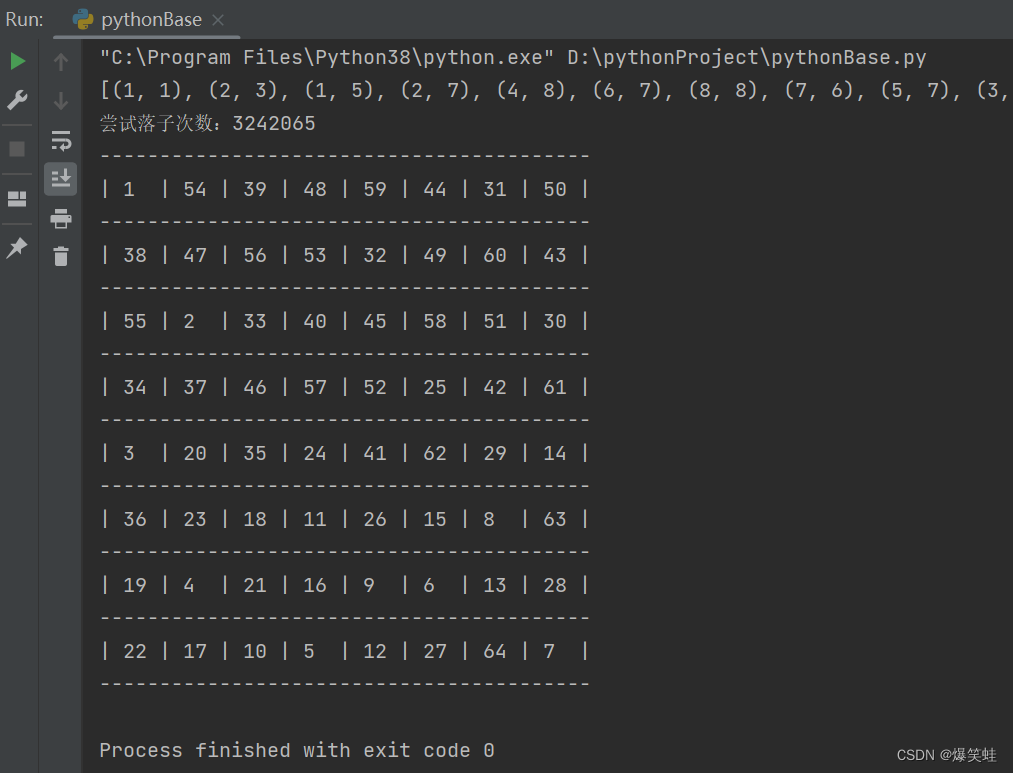
从运行结果来看,从第一个位置(1,1)开始共尝试落子3242065次找出了一种走完棋盘的方式。3242065看似很多次,但对于4的64次方来说小到忽略不计。也算是恰巧碰到了(1,1)这个位置,我尝试了(1,2)10分钟都没找到结果,我就手动终止了(浪费电)。你们的电脑比较好的话可以尝试一下多久出结果。(我的电脑尝试落子3242065次需要10秒钟,那么尝试落子4的64次方次大约需要33,282,130,589,010,443,001,514,556年,太难了!)
使用UI界面来动态打印行走方式
使用print来打印的结果,看起来密密麻麻的。不太方便观察,看久了花眼睛。所以我们可以使用tkinter来动态展示行走方式。UI界面的代码如下:
import time
import tkinter as tk
import threadingchess_list = [] # 存放落子位置的公共列表
times = 0 # 记录递归函数被调用次数的公共变量def return_location(x: int, y: int):"""返回可移动位置有那些:param x: x坐标:param y: y坐标:return: 可移动位置列表"""l_list = [] # 创建一个列表来存储可移动位置if x - 2 > 0 and y + 1 < 9: # 判断此位置是否超出棋盘l_list.append((x - 2, y + 1)) # 没有超出棋盘,则放入列表中if x - 1 > 0 and y + 2 < 9:l_list.append((x - 1, y + 2))if x + 1 < 9 and y + 2 < 9:l_list.append((x + 1, y + 2))if x + 2 < 9 and y + 1 < 9:l_list.append((x + 2, y + 1))if x + 2 < 9 and y - 1 > 0:l_list.append((x + 2, y - 1))if x + 1 < 9 and y - 2 > 0:l_list.append((x + 1, y - 2))if x - 1 > 0 and y - 2 > 0:l_list.append((x - 1, y - 2))if x - 2 > 0 and y - 1 > 0:l_list.append((x - 2, y - 1))return l_list # 返回可移动位置列表def full_chess_board(x: int, y: int):"""使用递归找出能填满整个棋盘的线路:param x: x坐标:param y: y坐标:return: bool,当递归深度为64时返回True,否则返回False"""global times # 声明公共变量times += 1 # 每调用一次递归函数times加一chess_list.append((x, y)) # 把落子位置放入公共列表中if len(chess_list) == 64: # 判断棋盘所有位置是否都已落子(递归深度是否为64)return True # 返回Truefor i in return_location(x, y): # 使用循环把可移动位置逐个输出if i not in chess_list: # 判断该位置在列表chess_list中是否存在if full_chess_board(i[0], i[1]): # 使用递归判断向下一个可移动位置移动是否可行(不断递归下去,能否达到64的深度)return True # 返回Truechess_list.remove((x, y)) # 此位置所有的分支都为绝路时,把此位置从公共列表中移除return False # 返回Falseclass ChessBoard:"""马踏棋盘动态展示使用tkinter中的方法创建UI界面界面中提供X和Y坐标的输入框,提供开始按钮使用full_chess_board函数计算出填充顺序"""canvas, coordinate_x, coordinate_y = None, None, Nonedef win(self):"""UI界面窗口初始化:return:"""root = tk.Tk() # 定义UI界面root.title('马踏棋盘') # 设置界面标题width = 605 # 设置界面宽度height = 630 # 设置界面高度win_width = root.winfo_screenwidth() # 获取电脑显示器宽度win_height = root.winfo_screenheight() # 获取电脑显示器高度x = win_width / 2 - width / 2 # 计算出UI界面左右边距y = win_height / 2 - height / 2 # 计算出UI界面上下边距root.geometry('%dx%d+%d+%d' % (width, height, x, y)) # 让UI界面居中显示tk.Label(root, text='X坐标:').grid(row=0, column=0) # 设置文本信息'X坐标:'位置第0行第0列self.coordinate_x = tk.Entry(width=10) # 设置X坐标输入框,宽度10self.coordinate_x.grid(row=0, column=1) # 位置第0行第1列tk.Label(root, text='Y坐标:').grid(row=0, column=2) # 设置文本信息'Y坐标:'位置第0行第2列self.coordinate_y = tk.Entry(width=10) # 设置Y坐标输入框,宽度10self.coordinate_y.grid(row=0, column=3) # 位置第0行第3列button = tk.Button(root, text='开始', command=self.thread_ui) # 设置开始按钮,绑定点击事件触发self.thread_ui函数button.grid(row=0, column=4) # 位置第0行第4列self.canvas = tk.Canvas(root, bg="SandyBrown", width=600, height=600) # 设置Canvas画布,背景为"SandyBrown",高宽600self.canvas.grid(row=1, column=0, rowspan=10, columnspan=10) # 位置第1行第0列,跨度10行10列for i in range(9):self.canvas.create_line(60, (60 * i + 60), 540, (60 * i + 60)) # 通过循环画9条间隔为60的竖线self.canvas.create_line((60 * i + 60), 60, (60 * i + 60), 540) # 通过循环画9条间隔为60的横线root.mainloop() # 持续刷新UI界面def draw_chess(self):"""绘制棋子行走过程:return:"""x = int(self.coordinate_x.get()) # 获取起始位置的X坐标y = int(self.coordinate_y.get()) # 获取起始位置的Y坐标full_chess_board(x, y) # 执行递归查找填充路线for i in chess_list: # 通过循环从公共列表中取出行走位置self.canvas.create_oval(15 + i[0] * 60, 15 + i[1] * 60, 45 + i[0] * 60, 45 + i[1] * 60, fill="black") # 画棋子time.sleep(1)self.canvas.create_oval(15 + i[0] * 60, 15 + i[1] * 60, 45 + i[0] * 60, 45 + i[1] * 60, fill="gray") # 画棋子def thread_ui(self):"""多线程执行任务:return:"""thread = threading.Thread(target=self.draw_chess) # 定义新线程thread.setDaemon(True) # 开启线程守护,主线程结束时子线程也会结束thread.start() # 执行新线程if __name__ == '__main__':chess_board = ChessBoard() # 实例画UI界面chess_board.win() # 调用界面窗口执行结果如下:

这篇关于python马踏棋盘的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






