Python机器学习之相异性度量

本文主要是介绍Python机器学习之相异性度量，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1 引言

相似性和相异性是机器学习中重要的概念，因为它们被许多数据挖掘技术所采用，比如常见的聚类、最近邻分类和异常检测等。在很多情况下，一旦我们计算出了特征向量的相似性或相异性，我们就不在需要原始数据了。这类方法通常将数据变换到相似性（相异性）空间，然后在做数据分析。

2 定义

相似度(similarity): 两个对象相似程度的数值度量，两个对象越相似，它们的相似度越高；通常取值为非负的，通常介于[0,1]之间。
相异度(disimilarity): 两个对象差异程度的数值度量，两个对象越相似，值越低，通常取值为非负的，最小相异度为0，上界不确定。通常使用术语距离（distance）用作相异性的同义词，距离常常用来表示特定类型的相异度。本文重点介绍常见的相异度计量函数。

3 欧式距离

欧氏距离是最易于理解的一种距离计算方法，源自欧氏空间中两点间的距离公式。其计算公式如下：
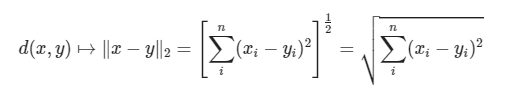
请添加图片描述
代码如下：

import numpy as np
from dissimilarity__utils import *def test_euclidean():eucl = lambda x, y: np.sum((x - y)**2, axis=1)**0.5x = np.array([0, 0])dA = eucl(x, yA)dB = eucl(x, yB).reshape(s.shape)plotDist(x, dA, dB, 'euclidean_distance', save=True)

其中 yA，yB的取值在 dissimilarity_utils里定义，如下：

r = 1
np.random.seed(123456)
y1A = np.random.uniform(-r, r, 8)
y2A = np.random.uniform(-r, r, 8)
yA = np.array([y1A, y2A]).T
M, N = 32j, 32j
s, t = np.mgrid[-r:r:N*8, -r:r:M*8]
yB = np.array([s.ravel(), t.ravel()]).T

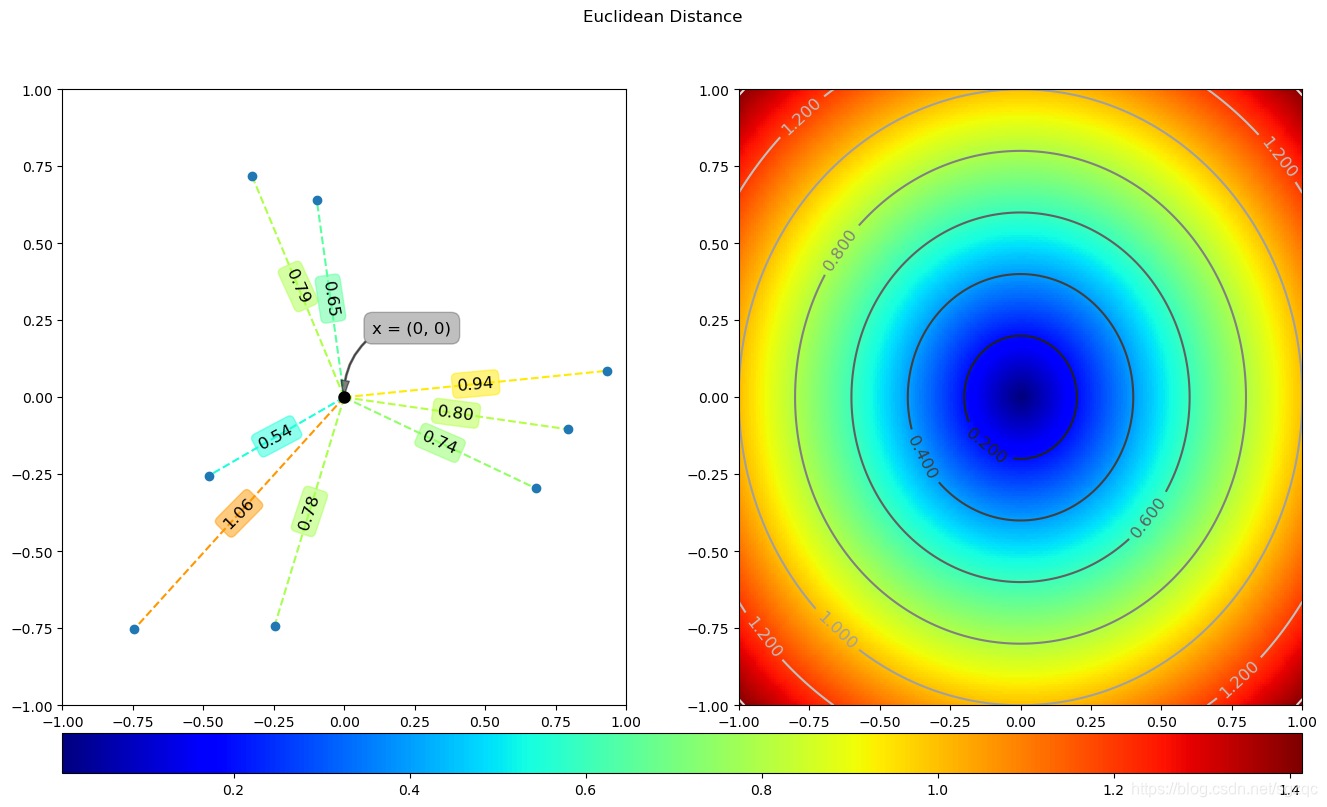
上述代码运行结果如下：
请添加图片描述

4 曼哈顿距离

曼哈顿距离的计算公式如下：
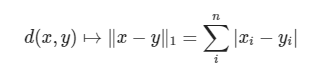
在这里插入图片描述
代码实现如下：

def test_manhattan():manh = lambda x, y: np.sum(np.absolute(x - y), axis=1)x = np.array([0, 0])dA = manh(x, yA)dB = manh(x, yB).reshape(s.shape)plotDist(x, dA, dB, 'manhattan_distance', save=True)

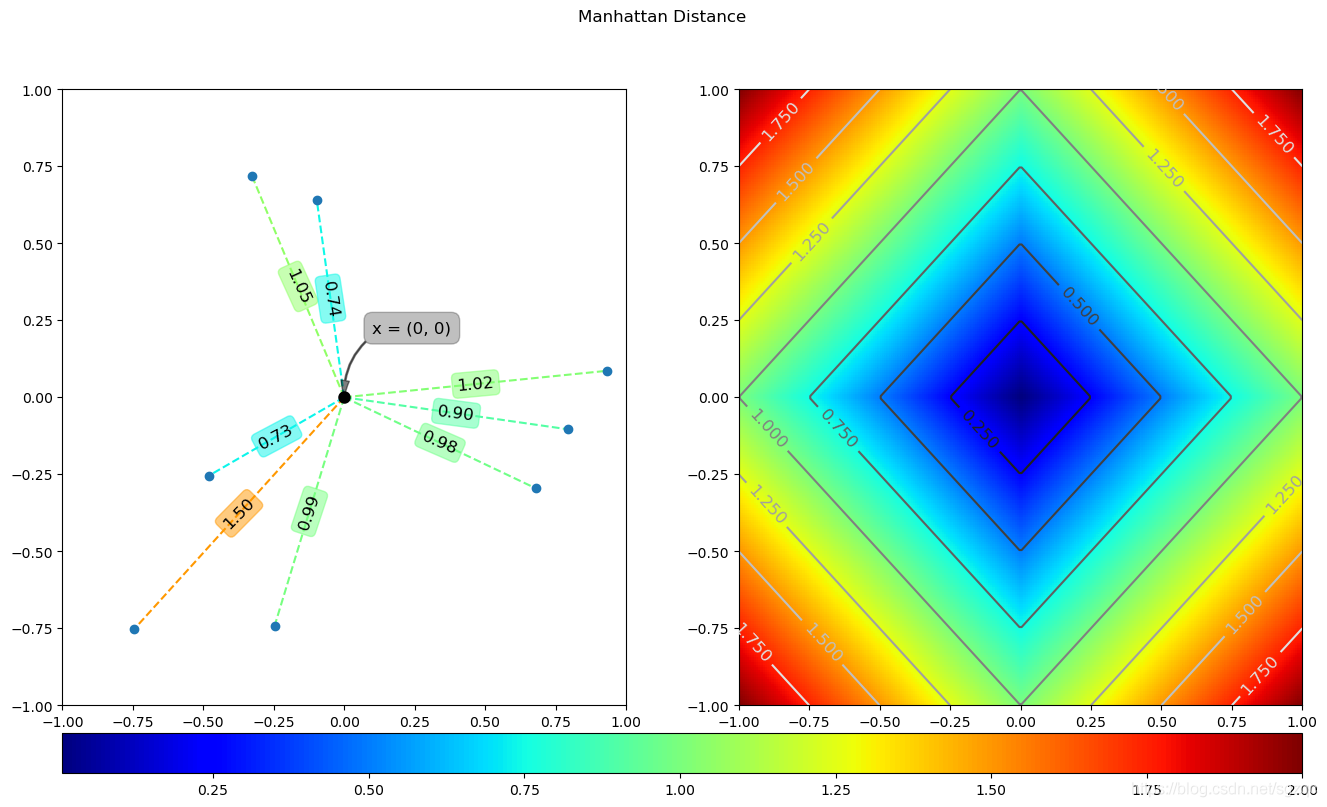
上述代码运行结果如下：
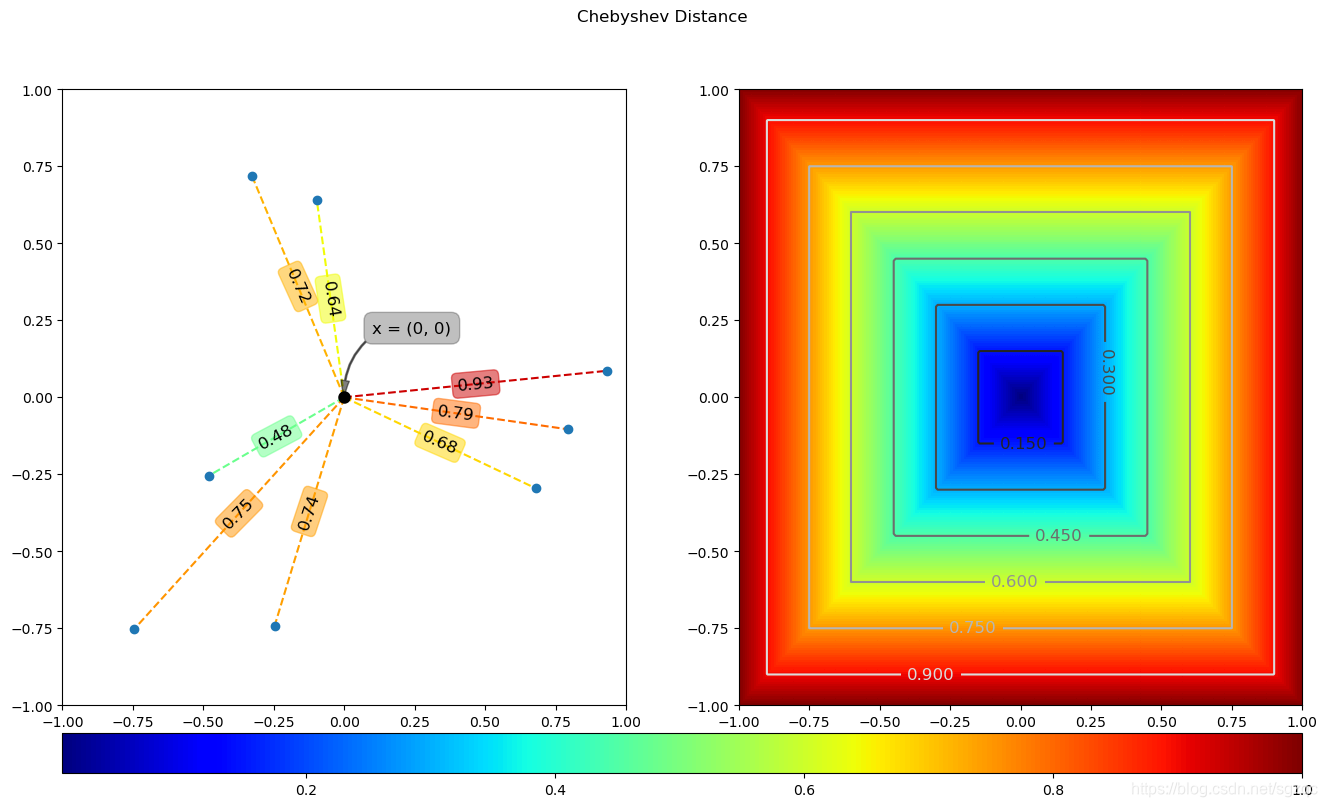
请添加图片描述

5 切比雪夫距离

国际象棋玩过么？国王走一步能够移动到相邻的8个方格中的任意一个。那么国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步？自己走走试试。你会发现最少步数总是max( | x2-x1 | , | y2-y1 | ) 步。有一种类似的一种距离度量方法叫切比雪夫距离。其计算公式如下：
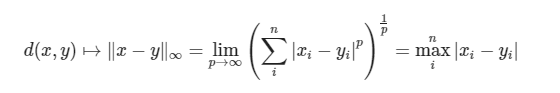
在这里插入图片描述
代码实现如下：

def test_chebyshev():cheb = lambda x, y: np.max(np.absolute(x - y), axis=1)x = np.array([0, 0])dA = cheb(x, yA)dB = cheb(x, yB).reshape(s.shape)plotDist(x, dA, dB, 'chebyshev_distance', save=True)

上述代码运行结果如下：
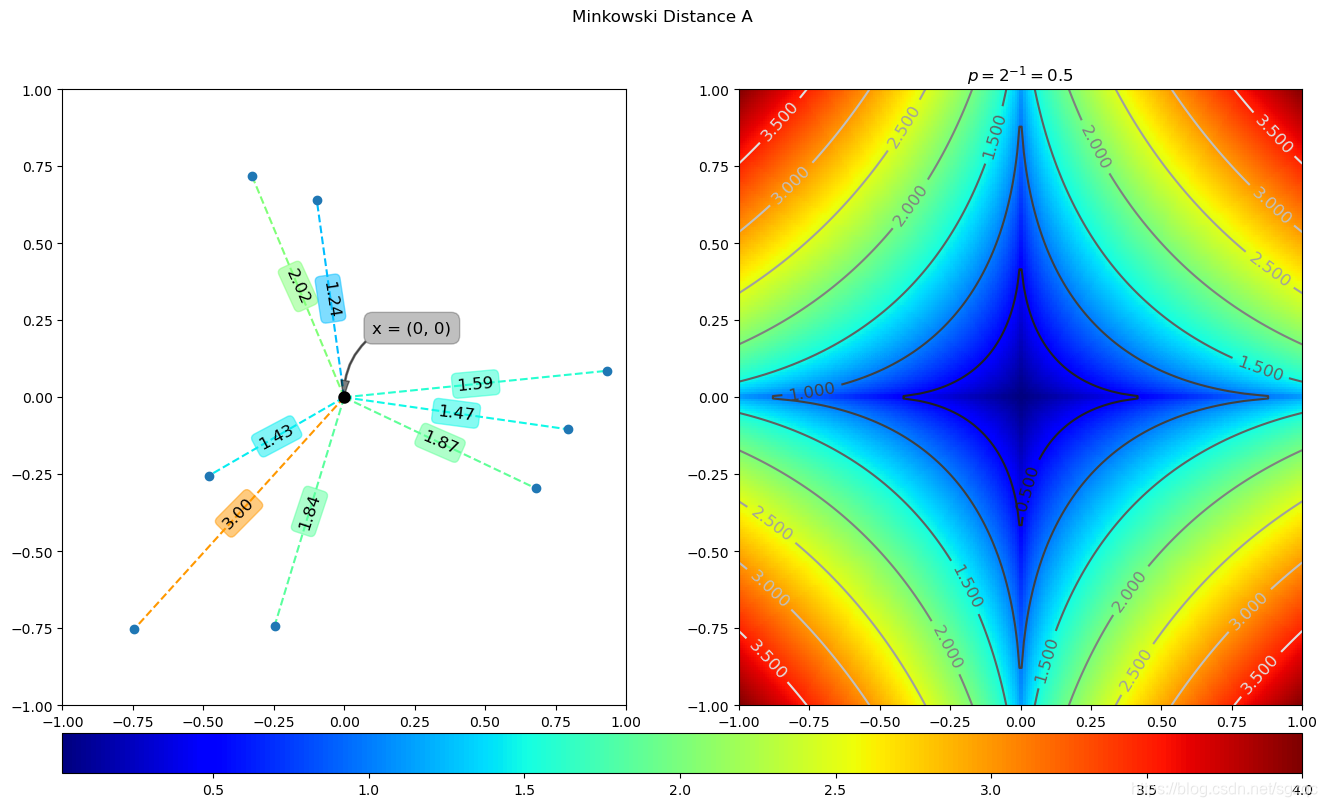
请添加图片描述

6 闵可夫斯基距离

闵氏距离不是一种距离，而是一组距离的定义。其计算公式如下：
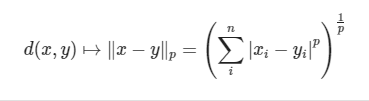
在这里插入图片描述
代码实现如下：

def test_minkowski():mink = lambda x, y, p: np.sum(np.absolute(x - y) ** p, axis=1) ** (1 / p)x = np.array([0, 0])p = 2 ** -1dA = mink(x, yA, p)dB = mink(x, yB, p).reshape(s.shape)plotDist(x, dA, dB, 'minkowski_distance_A', ctitle=r'$p=2^{0}{2}{1}={3}$'.format('{', '}', -1, p), save=True)

上述代码运行结果如下：
请添加图片描述
我们可以设置不同的p值，进而来对比不同p值下的结果图，代码如下：

def test_minkowski_multi():mink = lambda x, y, p: np.sum(np.absolute(x - y) ** p, axis=1) ** (1 / p)x = np.array([0, 0])fig, axes = plt.subplots(2, 4, sharex=True, sharey=True)for j, axs in enumerate(axes):for i, ax in enumerate(axs):index = i + 4 * jexp = index - 3pi = 2 ** expd = mink(x, yB, pi).reshape(s.shape)plotContour(ax, d,r'$p=2^{0}{2}{1}={3}$'.format('{', '}', exp, pi),fsize=8)figname = 'minkowski_distance_B'fig.suptitle(' '.join([e.capitalize() for e in figname.split('_')]))fig.savefig('_output/similarity_{}.png'.format(figname), bbox_inches='tight')

运行结果如下：
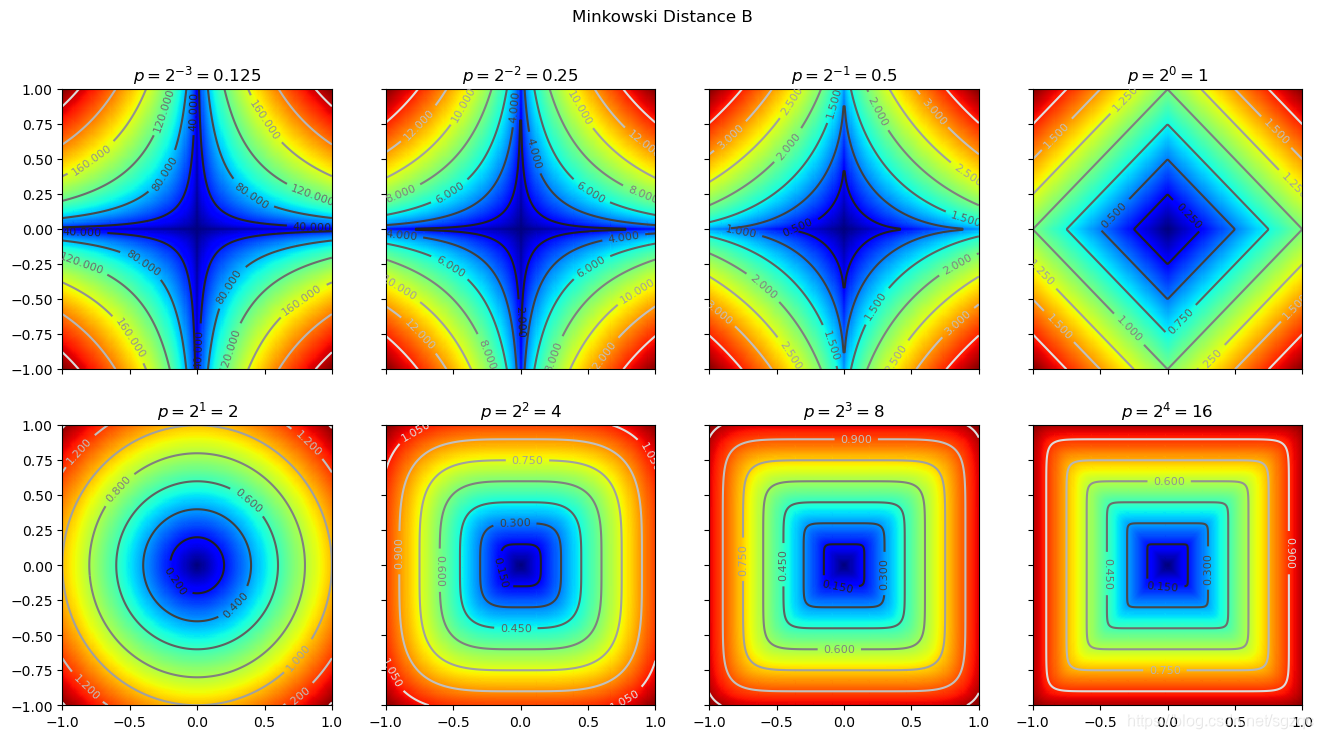
请添加图片描述

7 堪培拉距离

堪培拉距离可以是曼哈顿距离的加权版本，其计算公式如下：
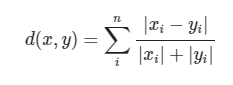
在这里插入图片描述
代码实现如下：

def canb(x, y):num = np.absolute(x - y)den = np.absolute(x) + np.absolute(y)return np.sum(num/den, axis = 1)def test_canberra():x = np.array([0.25, 0.25])dA = canb(x, yA)dB = canb(x, yB).reshape(s.shape)plotDist(x, dA, dB, 'canberra_distance', save=True)

上述代码运行结果如下：
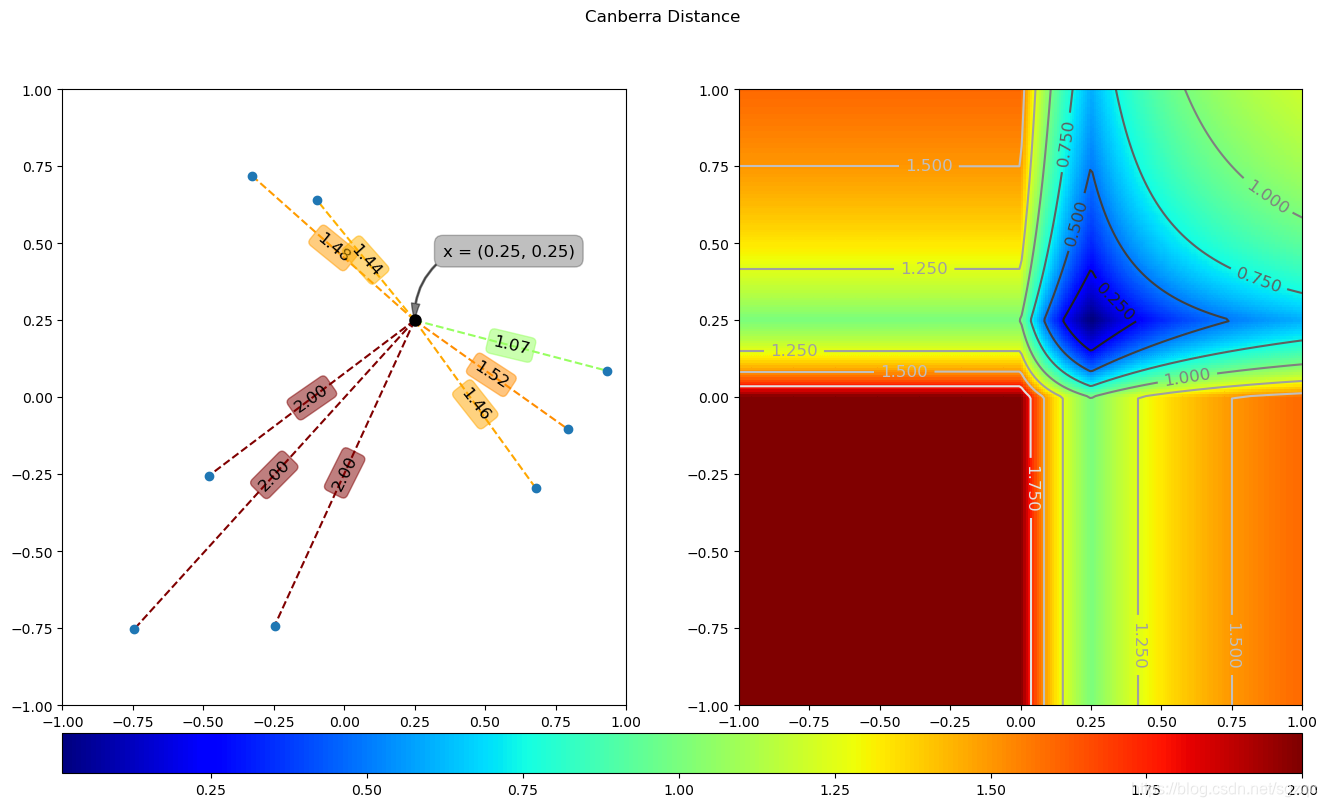
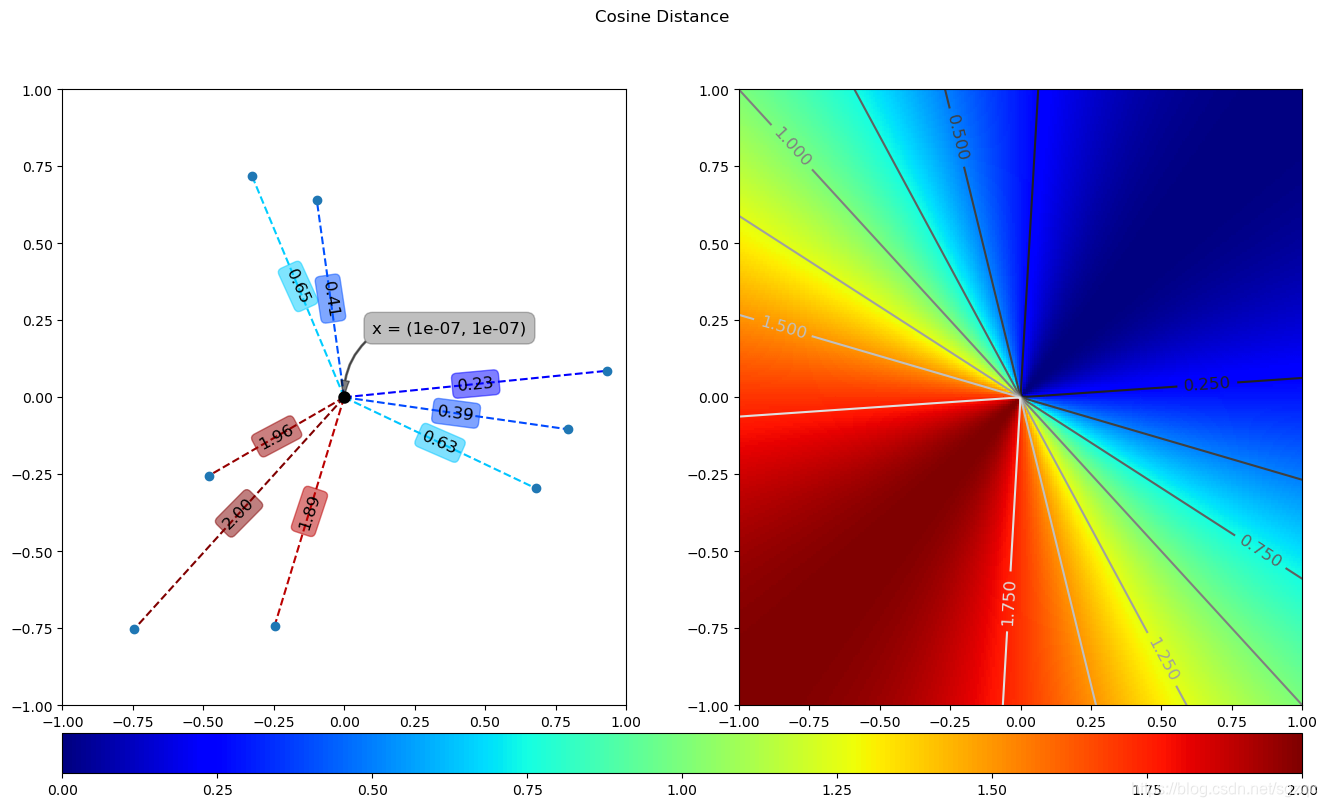
请添加图片描述

8 夹角余弦距离

几何中夹角余弦可用来衡量两个向量方向的差异，机器学习中借用这一概念来衡量样本向量之间的差异。其计算公式如下：
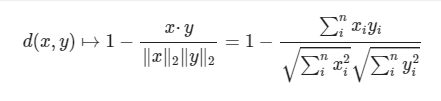
在这里插入图片描述
代码实现如下：

def coss(x, y):if x.ndim == 1:x = x[np.newaxis]num = np.sum(x*y, axis=1)den = np.sum(x**2, axis = 1)**0.5den = den*np.sum(y**2, axis = 1)**0.5return 1 - num/dendef test_cosine():x = np.array([1e-7, 1e-7])dA = coss(x, yA)dB = coss(x, yB).reshape(s.shape)plotDist(x, dA, dB, 'cosine_distance', save=True)