C++进阶篇4---番外-AVL树

本文主要是介绍C++进阶篇4---番外-AVL树，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、AVL树的概念

• 它的左右子树都是AVL树
• 左右子树的高度差(简称平衡因子)的绝对值不超过1(只能是-1/0/1)

【注意】平衡因子是用右子树的高度减去左子树的高度得到的

 

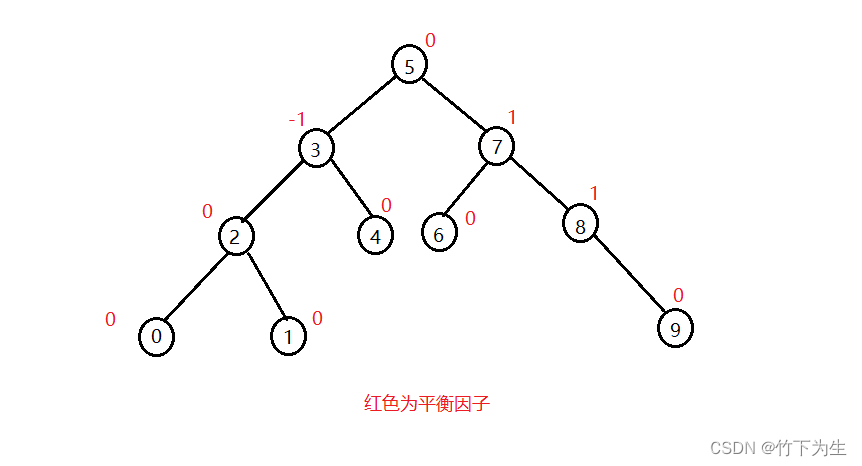
二、AVL树结点的定义

template<class K,class V>
struct AVLTreeNode {AVLTreeNode* _left;AVLTreeNode* _right;AVLTreeNode* _parent;pair<K, V> _kv;int _bf;AVLTreeNode(const pair<K,V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr),_kv(kv),_bf(0){}
};

 三、AVL树的插入

AVL树就是在二叉搜索树的基础上引入了平衡因子，因此AVL树也可以看成是二叉搜索树。

AVL树的插入过程可以分为两步：

1. 按照二叉搜索树的方式插入新节点
2. 调整节点的平衡因子

template<class K,class V>
class AVLTree {typedef AVLTreeNode<K, V> Node;
public:bool insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if(cur->_kv.first>kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(kv);cur->_parent = parent;if (parent->_kv.first > kv.first ){parent->_left = cur;}else{parent->_right = cur;}//看树是否还保持平衡while (parent){//先调整平衡因子---因为插入的结点是叶子节点，所以父结点的平衡因子必然发生变化//在根据平衡因子的计算公式height_r - height_l，判断平衡因子的变化if (parent->_left == cur){parent->_bf--;}else{parent->_bf++;}//看是否需要调整以及如何调整//...}}
private:Node* _root = nullptr;
};

上面代码的插入逻辑和二叉搜索树很相似，这里不多讲了(忘记的或者不了解的可以去看二叉搜索树)，主要看如何判断树是否平衡以及如何调整使得树保持平衡

这里主要分三种情况：

1、父节点的平衡因子变成0，则树保持平衡，不需要变化

解释:父节点的平衡因子变成0，说明之前未正负1，只有如下两种情况

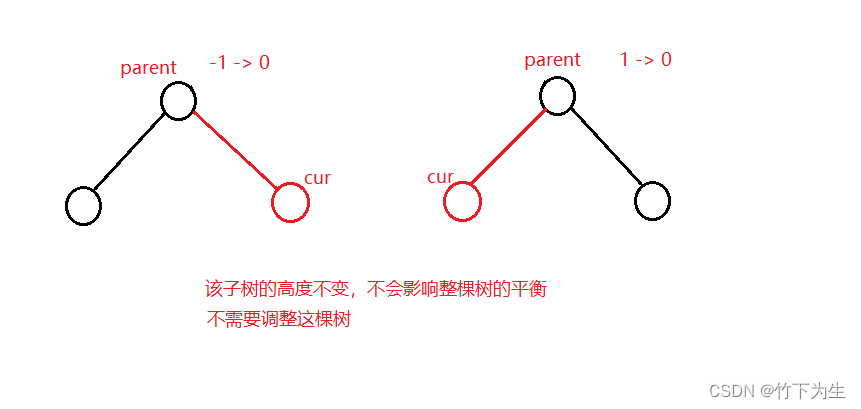
2、父节点的平衡因子变成正负1，则该子树的高度发生变化，但该子树依旧平衡，要看它的父节点所在的子树是否还能保持平衡

 

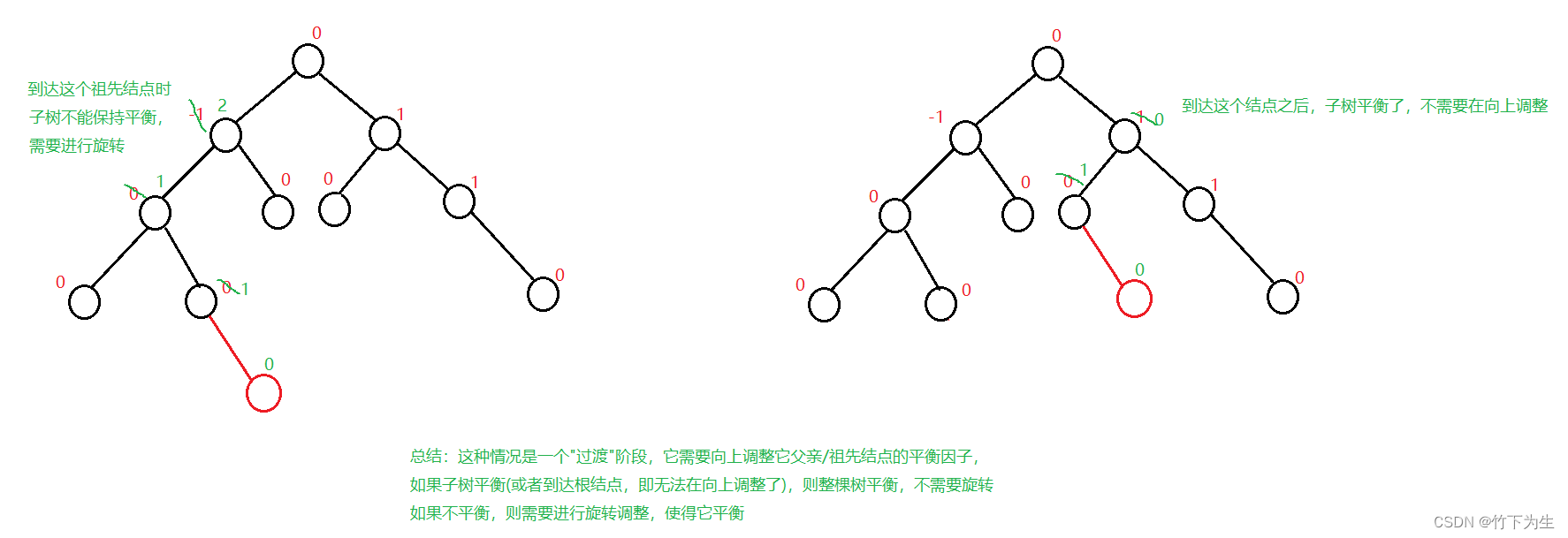
3、父结点的平衡因子变成正负2，则该子树的不能保持平衡，需要进行旋转调整

template<class K,class V>
class AVLTree {typedef AVLTreeNode<K, V> Node;
public:bool insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if(cur->_kv.first>kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(kv);cur->_parent = parent;if (parent->_kv.first > kv.first ){parent->_left = cur;}else{parent->_right = cur;}//看树是否还保持平衡while (parent){//先调整平衡因子if (parent->_left == cur){parent->_bf--;}else{parent->_bf++;}if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//分4种情况:左单旋，右单旋，先左旋在右旋，先右旋在左旋//...//旋转完成后子树就平衡了=> 整个树都平衡了，直接退出循环break;}else{//如果进入这里，说明前面的代码出错assert(0);}}}
private:Node* _root = nullptr;
};

 四、旋转调整

1、新节点插入较高右子树的右侧---右右：左单旋

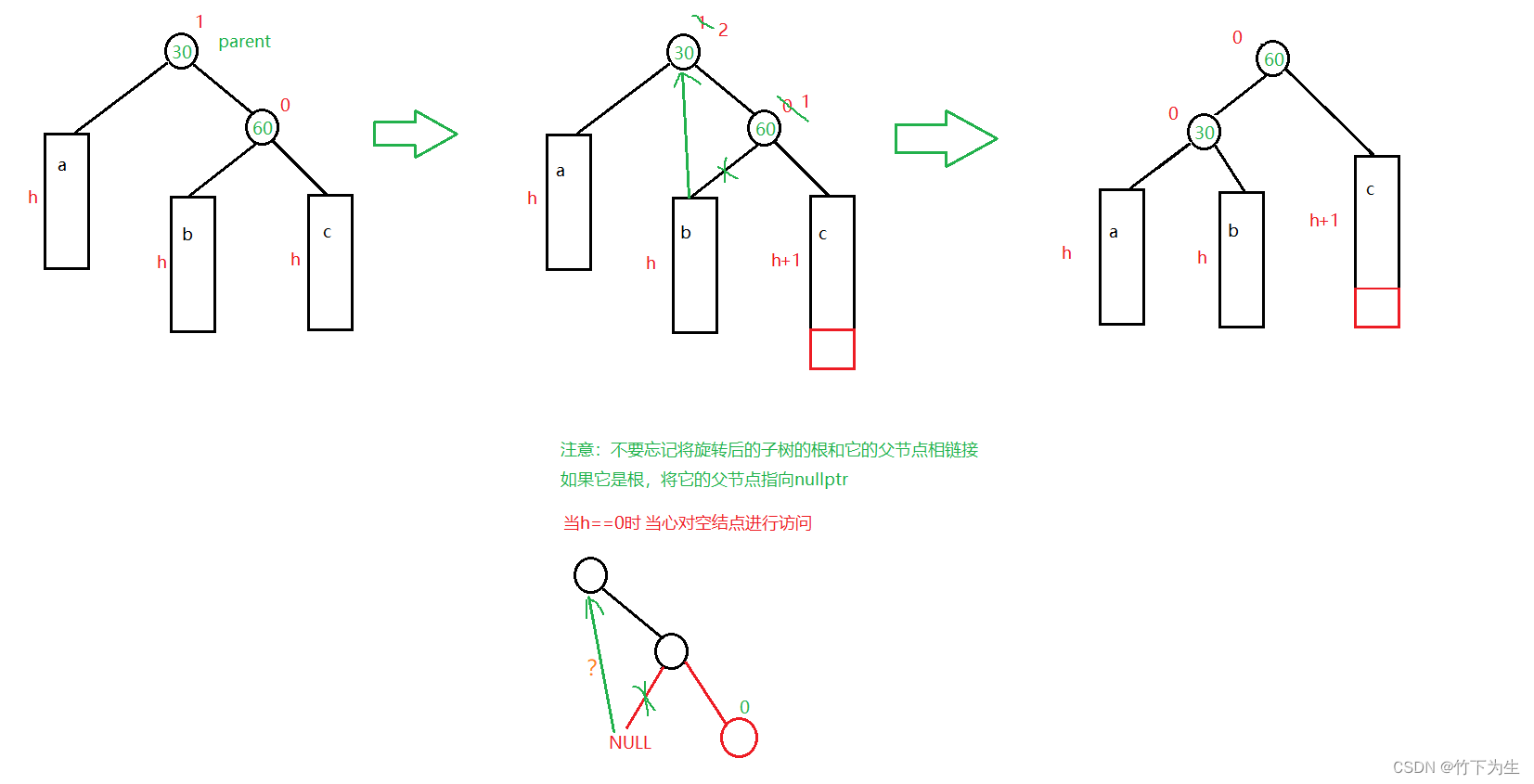
代码如下

	void _RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;Node* pParent = parent->_parent;subR->_left = parent;parent->_parent = subR;if (subRL)//注意h==0的情况subRL->_parent = parent;if (_root == parent){_root = subR;subR->_parent = nullptr;}else{subR->_parent = pParent;if (pParent->_left == parent){pParent->_left = subR;}else{pParent->_right = subR;}}subR->_bf = parent->_bf = 0;}

2、 新节点插入较高左子树的左侧---左左：右单旋

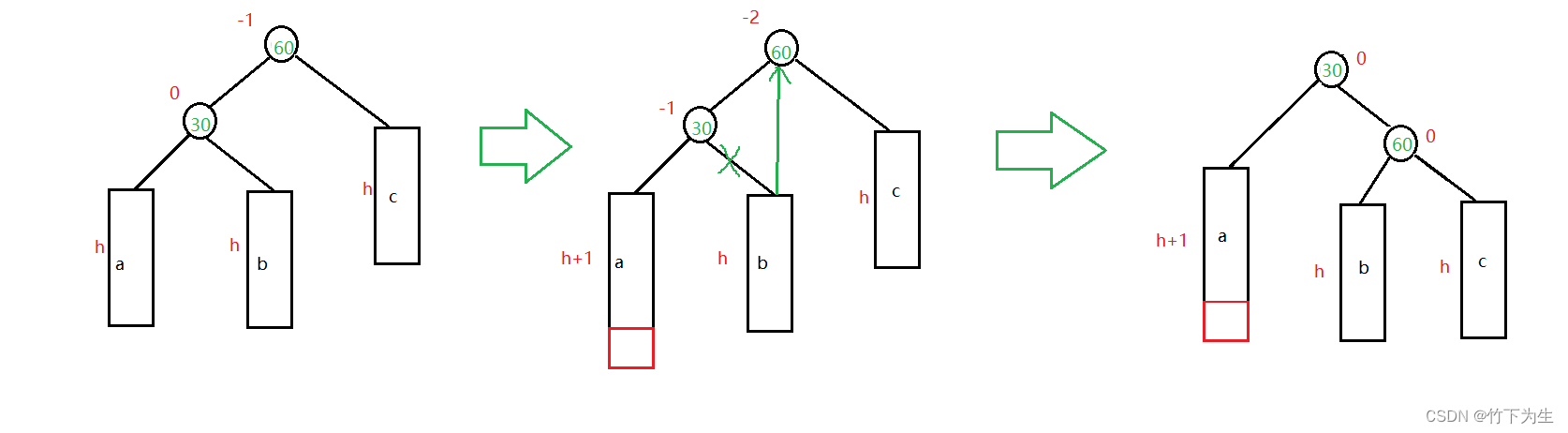
注意事项同上。

代码如下 

void _RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;Node* pParent = parent->_parent;subL->_right = parent;parent->_parent = subL;if (subLR)//注意h==0的情况subLR->_parent = parent;if (_root == parent){_root = subL;subL->_parent = nullptr;}else{subL->_parent = pParent;if (pParent->_left == parent){pParent->_left = subL;}else{pParent->_right = subL;}}subL->_bf = parent->_bf = 0;}

3、 新节点插入较高右子树的左侧---右左：先右单旋再左单旋

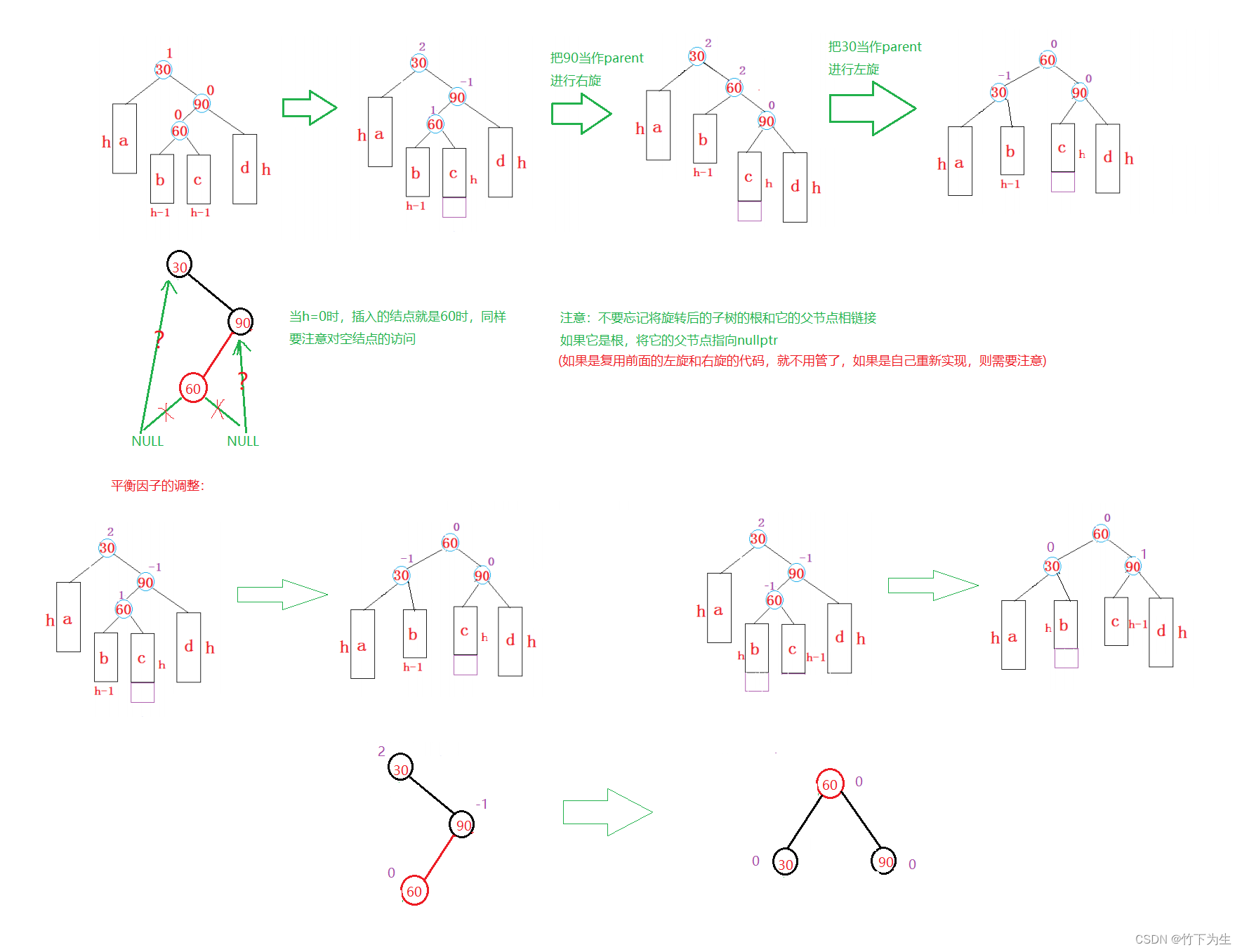
代码如下

	void _RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;//提前记录，防止在旋转时被修改_RotateR(parent->_right);_RotateL(parent);if (bf == 0){parent->_bf = subR->_bf = subRL->_bf = 0;}else if (bf == 1){parent->_bf = -1;subR->_bf = subRL->_bf = 0;}else{subR->_bf = 1;parent->_bf = subRL->_bf = 0;}}

 4.新节点插入较高左子树的右侧---左右：先左单旋再右单旋

这个留给读者思考 

附：

//完整版代码
template<class K,class V>
struct AVLTreeNode {AVLTreeNode* _left;AVLTreeNode* _right;AVLTreeNode* _parent;pair<K, V> _kv;int _bf;AVLTreeNode(const pair<K,V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr),_kv(kv),_bf(0){}
};template<class K,class V>
class AVLTree {typedef AVLTreeNode<K, V> Node;
public:bool insert(const pair<K,V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(kv);cur->_parent = parent;if (parent->_kv.first > kv.first){parent->_left = cur;}else{parent->_right = cur;}while (parent){if (parent->_left == cur){parent->_bf--;}else{parent->_bf++;}if (parent->_bf == 0)//为0，说明之前_bf=-1/1,即子树的高度没有发生变化{break;}	else if (parent->_bf == 1 || parent->_bf == -1)//为正负1，说明之前_bf=0，即子树的高度发生变化，并且会影响到上层祖宗结点{cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2)//为正负2，树明显不平衡，需要旋转调整{if (parent->_bf == 2 && cur->_bf == 1)//如果该子树的严格右边高，则左单旋{_RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == -1)//如果该子树的严格左边高，则右单旋{_RotateR(parent);}else if (parent->_bf == -2 && cur->_bf == 1)//左右旋{_RotateLR(parent);}else if (parent->_bf == 2 && cur->_bf == -1)//右旋左旋{_RotateRL(parent);}break;//旋转之后整个树就平衡了，直接跳出循环}else{//这种情况不可能发生，如果发生就说明程序出错assert(false);}}return true;}void _RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;_RotateL(parent->_left);_RotateR(parent);if (bf == 1){subL->_bf = -1;subLR->_bf = parent->_bf = 0;}else if(bf == -1){parent->_bf = 1;subL->_bf = subLR->_bf = 0; }else//bf==0，插入的结点就是subLR{parent->_bf = subL->_bf = subLR->_bf = 0;}}void _RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;_RotateR(parent->_right);_RotateL(parent);if (bf == 1){parent->_bf = -1;subR->_bf = subRL->_bf = 0;}else if(bf == -1){subR->_bf = 1;parent->_bf = subRL->_bf = 0;}else //bf==0，插入的结点就是subLR{parent->_bf = subR->_bf = subRL->_bf = 0;}}//右单旋void _RotateR(Node*parent){Node* subL = parent->_left;//找到要作为新根的结点Node* pParent = parent->_parent;//找到该子树的父亲结点Node* subLR = subL->_right;subL->_right = parent;parent->_parent = subL;parent->_left = subLR;if (subLR)subLR->_parent = parent;if (_root == parent)//如果是根{_root = subL;subL->_parent = nullptr;}else{subL->_parent = pParent;if (pParent->_left == parent){pParent->_left = subL;}else{pParent->_right = subL;}}parent->_bf = subL->_bf = 0;}//左单旋void _RotateL(Node* parent){Node* subR = parent->_right;//找到要作为新根的结点Node* pParent = parent->_parent;//找到该子树的父亲结点Node* subRL = subR->_left;//找到要被"过继"的孩子结点subR->_left = parent;if (subRL)//如有"过继"结点subRL->_parent = parent;parent->_parent = subR;parent->_right = subRL;if (_root == parent)//如果是根{_root = subR;subR->_parent = nullptr;}else{subR->_parent = pParent;if (pParent->_left == parent){pParent->_left = subR;}else{pParent->_right = subR;}}parent->_bf = subR->_bf = 0;}bool Isbalance(){return _Isbalance(_root);//return _Isbalance(_root) >= 0;}bool _Isbalance(Node*root){if (root == nullptr)return true;int left = _Height(root->_left);int right = _Height(root->_right);if (abs(right - left) > 1){cout << root->_kv.first << ":" << root->_kv.second << endl;return false;}if (right - left != root->_bf){cout << root->_kv.first << ":"<< "平衡因子出错" << endl;return false;}return _Isbalance(root->_left) && _Isbalance(root->_right);}size_t size(){return _size(_root);}size_t Height(){return _Height(_root);}private:size_t _Height(Node*root){if (root == nullptr)return 0;return max(_Height(root->_left),_Height(root->_right)) + 1;}size_t _size(Node* root){if (root == nullptr)return 0;return 1 + _size(root->_left) + _size(root->_right);}//如果单纯判断是否平衡可以这么写，-1表示不平衡，>=0表示平衡//int _Isbalance(Node* root)//{//	if (root == nullptr)//		return 0;//	int left = _Isbalance(root->_left);//	if (left < 0) return -1;//	int right = _Isbalance(root->_right);//	if (right < 0) return -1;//	if (abs(right - left) > 1 || right - left != root->_bf)//	{//		return -1;//	}//	return max(left, right) + 1;//}
private:Node* _root = nullptr;
};

这篇关于C++进阶篇4---番外-AVL树的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---