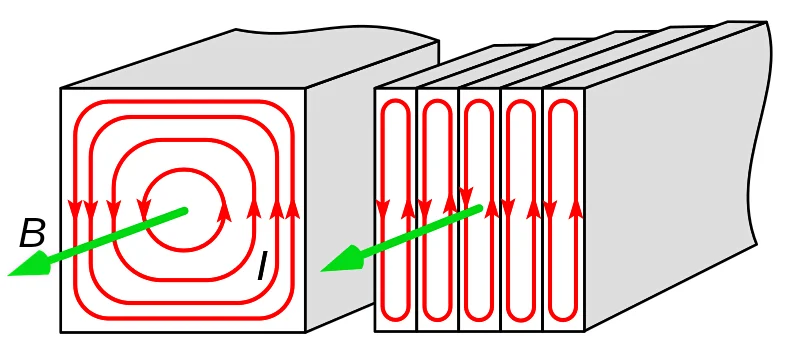
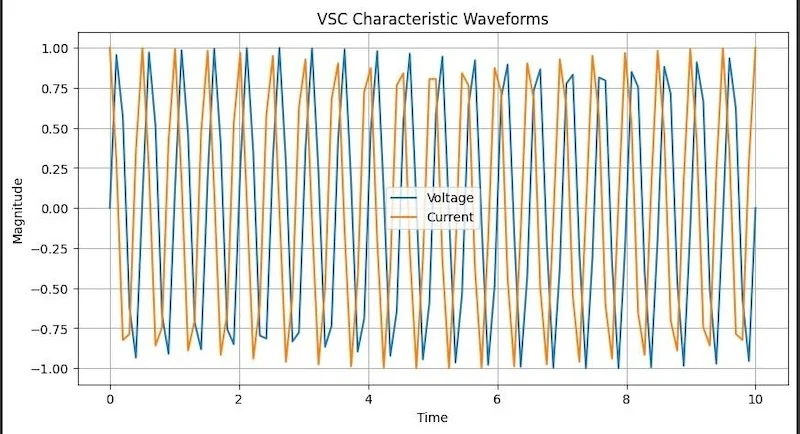
本文主要是介绍电机学2——变压器(中),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
电机学2——变压器(中)
- 变压器的负载运行
- 变压器的负载运行过程
- 负载运行时的方程式
- 变压器的归算
- 归算的目的
- 归算的方法和过程
- 变压器的等效电路
- 变压器的T型等效电路
- 变压器的其他等效电路。
- 变压器的相量图
- T型等效电路的相量图
- 最简化等效电路的相量图
- 变压器参数测定
- 变压器的参数及测定方法
- 空载实验
- 短路实验
变压器的负载运行
变压器的负载运行过程
1、空载 → \rightarrow →负载
原端空载运行稳态后闭合开关 K 2 K_2 K2,副端灯亮,得到能量
变化过程: i 2 ↑ i_2\uparrow i2↑( F 2 ≠ 0 F_2\ne0 F2=0),总的磁势变化,磁通,电势,电流变化,最后达到电磁平衡;原端: i 0 → i 1 i_0\rightarrow i_1 i0→i1
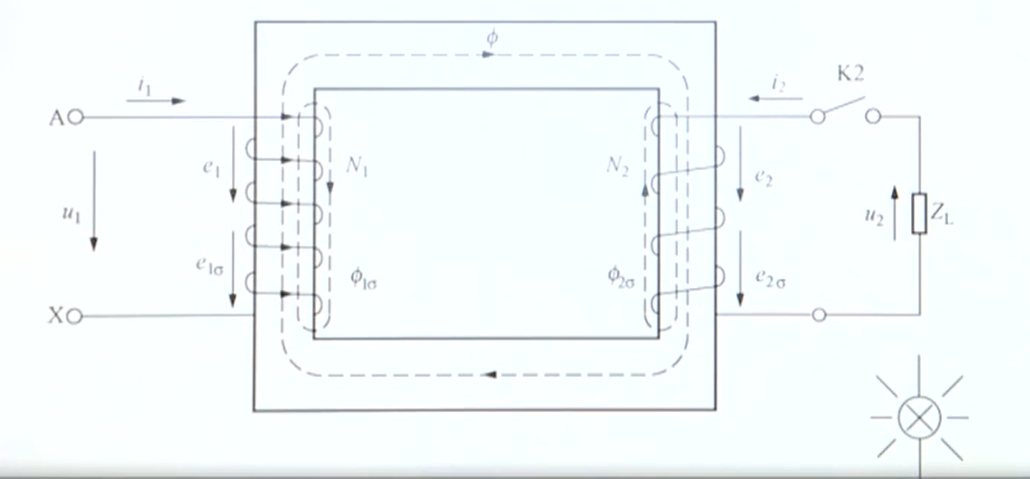
2、负载时物理量的耦合关系
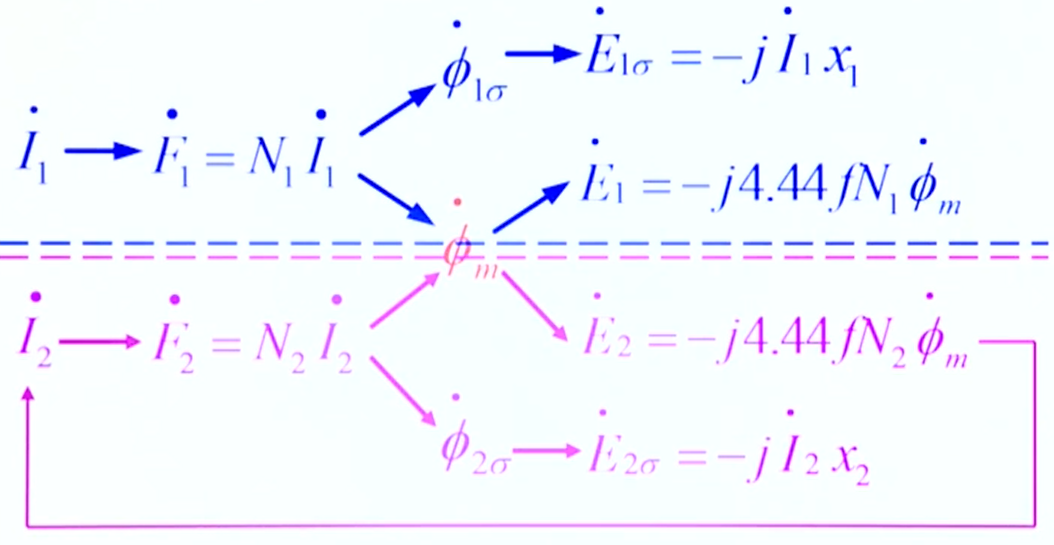
3、副端参数的变化
关心的问题: i 2 = ? ; u 2 = ? ; p 2 = ? i_2=?;u_2=?;p_2=? i2=?;u2=?;p2=?如何传递的?(为了方便分析,忽略漏阻抗 Z 1 Z_1 Z1和 Z 2 Z_2 Z2)
(1) i 2 = ? i_2=? i2=?
当 E 1 ≈ U 1 = c o n s t E_1\approx U_1=const E1≈U1=const时,则 Φ m ≈ c o n s t \Phi_m\approx const Φm≈const,闭合磁路上, Σ Φ m R m = Σ F = c o n s t \Sigma\Phi_mR_m=\Sigma F=const ΣΦmRm=ΣF=const
F 1 + F 2 = F 0 F_1+F_2=F_0 F1+F2=F0(空载和负载磁势不变)
I ˙ 1 N 1 + I ˙ 2 N 2 = I ˙ 0 N 1 \dot I_1N_1+\dot I_2N_2=\dot I_0N_1 I˙1N1+I˙2N2=I˙0N1
I ˙ 1 + 1 k I ˙ 2 = I ˙ 0 \dot I_1+\frac{1}{k}\dot I_2=\dot I_0 I˙1+k1I˙2=I˙0
假设原端电流中增加一个负载分量:
I ˙ 1 = I ˙ 0 + I ˙ 1 L \dot I_1=\dot I_0+\dot I_{1L} I˙1=I˙0+I˙1L
带入上式得 { I ˙ 1 L N 1 + I ˙ 2 N 2 = 0 I ˙ 2 = − k I ˙ 1 L \{\begin{aligned}\dot I_{1L}N_1+\dot I_2N_2=0\\\dot I_2=-k\dot I_{1L}\end{aligned} {I˙1LN1+I˙2N2=0I˙2=−kI˙1L
I 1 I_1 I1中 I 1 L I_{1L} I1L占绝对大的比例
结论:原副端电流是有联系的(副端电流大小决定着原端电流大小)
负载以后,原端电流上升很多(符合能量守恒定律)
(2) u 2 = ? u_2=? u2=?
副端电压方程式
U ˙ 2 = E ˙ 2 + E ˙ 2 σ − I ˙ 2 r 2 \dot U_2=\dot E_2+\dot E_{2\sigma}-\dot I_2r_2 U˙2=E˙
这篇关于电机学2——变压器(中)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!