统计学习（李航）笔记（编辑中）

1 工具

1.1 EM算法

em算法是通过求期望最大的算法。通过样本来推测参数（迭代直至收敛），k-means是em的一种特殊情况。
输入：观测变量数据Y，隐变量数据Z，联合分布P(Y,Z|$\theta$),条件分布P(Z|Y,$\theta$)
输出：$\theta$ 参数

1. 选择${\theta }^{(0)}$ 初值。
2. E步（求期望Z|Y）：$Q(\theta ,{\theta }^{(i)})=E_Z[logP(Y,Z;\theta )|Y;,{\theta }^{(i)}]={\sum }_{z}P(Z|Y;,{\theta }^{(i)})logP(Y,Z;\theta )$
3. M步（求最大期望时的$\theta$）:${\theta }^{(i+1)}=argmaxQ(\theta ,{\theta }^{(i)})$
4. 重复23直至收敛

EM算法具有单调性和收敛性。

1.2 KKT条件

KKT是最优化求解的一个工具。

1. min f(x)只需要求导可解。
2. min f(x), st. h(x)=0, 使用拉格朗日乘子法可解。
3. min f(x), st. $C_i(x)⩽0,h_j(x)=0$,KKT可解。

KKT条件使用广义拉格朗日求解如下：

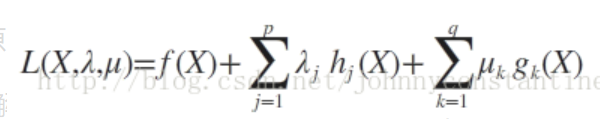
此时若要求解上述优化问题，必须满足下述条件（也是我们的求解条件）：

这些求解条件就是KKT条件。(1)是对拉格朗日函数取极值时候带来的一个必要条件，(2)是拉格朗日系数约束（同等式情况），(3)是不等式约束情况，(4)是互补松弛条件，(5)、(6)是原约束条件。

1.3 奇异矩阵SVD

$A=U\sum V^T$

1.4 马尔科夫链MCMC

已知分布（复杂），生成相应的随机样本序列。
输入：目标分布密度函数
输出：符合分布的随机样本x…

2 有监督学习

2.1 感知机（二分类）

$f(x)=sign(w^{T}x+b)$
损失函数为 $-{\sum }_{i\in M}{y}_i(w^{T}x+b)$ 分类错误的点到超平面的距离。
优化策略为求损失函数最小时候的w和b，分别求导梯度下降：

算法：

• 输入：$(x_1,y_1),(x_2,y_2).......$,x是n维向量，y为分类变量
• 输出：w，b
  1.初始选择w,b
  2.加入训练数据
  3.梯度下降
  4.重复23步骤，直至分类正确。

2.2 KNN近邻（分类）

2.3 朴素贝叶斯

2.4 决策树

2.5 提升Boosting

2.6 逻辑回归

2.7 支持向量机

2.8 HMM蒙特卡洛马尔可夫

3 无监督学习

3.1 聚类

• 度量距离的方法：闵氏距离（$(\sum （x_i-x_j{）}^p{)}^{1/p}$）、欧氏距离（p=2）、相关系数、余弦相似度
• 类别G、距离T：$x_i,x_j\in G\to d_{x_i{x}_j}<T$
• 层次聚类：聚合（n个类聚）、分裂（1个类分）
  例：1、首先计算距离矩阵。2、合并距离最小的两个类组成新的类。3、重新计算距离矩阵。4、重复23步骤。
• k-means聚类
  例：1、随机选取k个质心。2、计算距离，归类。3、重新计算质心。4、重复23直至收敛。

3.2 主成分PCA

奇异值分解

3.3 潜在语义分析

给定一个文本，用向量空间内积度量文本之间的’语义相似度‘。
矩阵乘法X=T*Y

• X单词文本矩阵（m单词*n文本）：无法处理一词多义
• T话题矩阵（m单词*k话题）
• Y话题文本矩阵（k话题*n文本）：文本在话题向量空间的权重

3.4 PageRank

定义：网页经济和的函数表示网页的重要程度。值越高，网页越重要，从质和量两方面衡量。
质：被越重要的网站链接引用。
量：被引用的多。