双面渲染美翻了！零基础也能学会，源码直接带走…

你是否也曾好奇？

如果要渲染一片树叶，但树叶的两个面的外观通常是不同的，如何做到正反面效果不一样呢？

图片来自网络

如果要渲染像下图中某个对象的一部分，又当如何做呢？

细节指引： 图中，处于虚空连接口背后的龙是看得见的，从虚空连接口钻出来的龙只能看到一部分身体。

3D图形管线在进行背面裁剪的时候，是如何判断一个三角形是正对摄像机还是背对摄像机的呢？如下图所示：

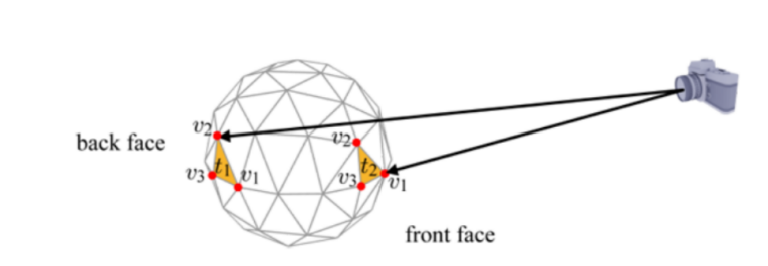
麒麟小贴士： 背面裁剪是图形管线在 vs 之后和 fs 之前做的一次预剔除处理。
通过背面裁剪，图形管线可以在渲染模型的时候，剔除背对着我们的面，（比如一个正对着我们的人物模型，他的背面），以提升渲染性能。

看完本文后，你将掌握以下知识点：

• 点法式平面表示法

• 正背面判定

• 双面材质

• 自定义裁剪面

三维空间平面表示法

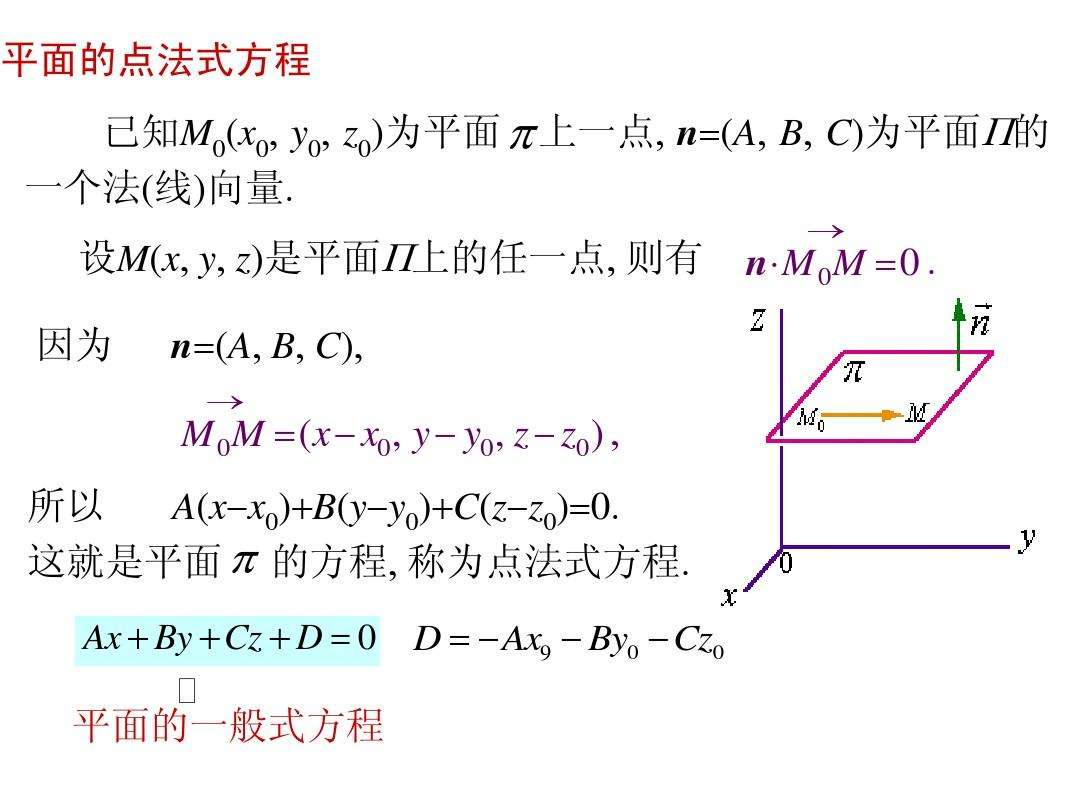
在 3D 游戏编程相关的数学书里，我们可以很容易找到上图中的内容。

它用代数的方式解释了为什么可以用 Ax + By + Cz + D = 0 来表示平面。

A,B,C 是平面的单位化法向量的 XYZ 值，它决定了平面的正方向，D 为坐标原点到平面的距离的相反数。

将一个点从原点朝向量（A,B,C）正方向移动 -D 的距离，可以得到平面上的一个点，因此这个表示法被称为：点法式。

麒麟小贴士： 许多教材中，对矩阵运算和相关公式都是做的代数推导，晦涩难懂。但数学是对事物规律的体现，代数推导不是唯一解。

对于 3D 图形学中的诸多运算，可以使用空间几何来推导。空间几何可以使我们理解起来更加简单直观。

像反射公式、镜像矩阵、坐标系转换、投影矩阵等与平面相关的原理，大家不妨试试用几何原理理解一次。

接下来，我们尝试着用空间几何的方式理解一次平面公式（可能需要一些空间想象力）：

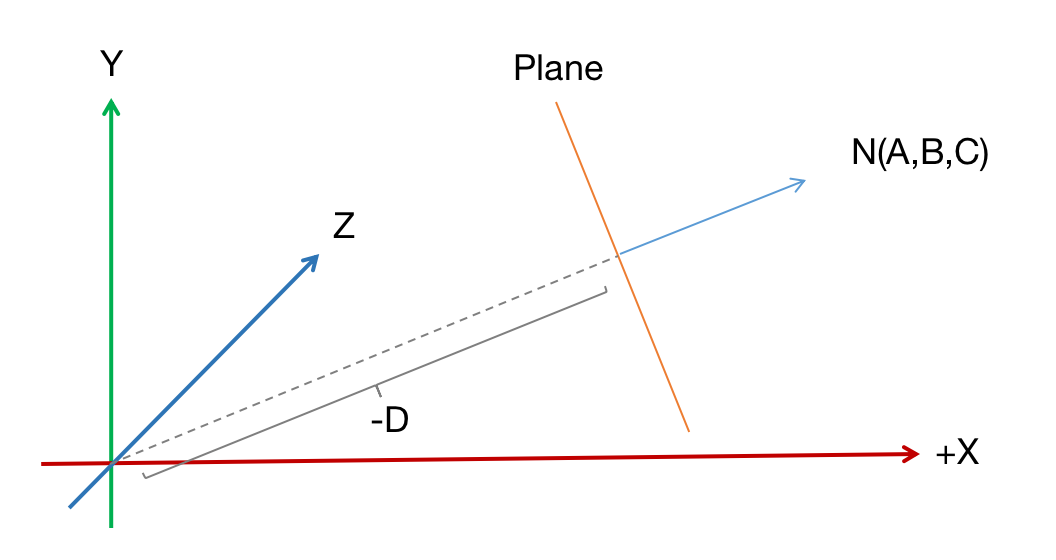
1、在原点处，向任意方向（A,B,C）发射出一条射线，则这条射线的起点为记P0(0,0,0)，方向记为 Direction(A,B,C)。

2、我们发现，这条射线可以确定一个唯一的面：经过原点且垂直于条射线方向。那么 Direction(A,B,C) 恰好就是这个面的法向量。

3、将这个射线的起点沿 Direction(A,B,C) 正向或者负向移动，可以调节它在空间中的位置。假设我们移动到了点 P0(x0,y0,z0)，由投影原理可知，此时射线起点到原点的距离 d 的计算方式为：

• d = dot(Direction,P0)

• => d = A * x0 + B * y0 + C * z0

此种情况下，我们依然可以得到一个 经过点 P0 且与 Direction 垂直的唯一面。

4、由于Direction是空间中任意方向，P0 是射线上的任意点，我们可以得到一个结论： 一个向量和一个距离坐标系原点的值可以用来表示三维空间中的任意平面。

5、如果一个点 P(x,y,z) 在平面上，可知：

• Ax + By + Cz = d

• => Ax + By + Cz - d = 0

6、不难看出 Ax + By + Cz 刚好是 Direction 与 P 的点乘，而在 3D 空间运算中，在参与矩阵运算时，点的表示法为 P(x,y,z,1)。因此， 若将平面记作四维向量 Plane(A,B,C,D) 其中 (D = -d)，则恰好满足点乘运算规则，也完全符合代数推导结果：Ax + By + Cz + D = 0。

7、每个平面，都会将空间一分为二，我们将法线方向的空间视为平面的正面，法线反方向的空间视为平面的背面。

正背面的判定

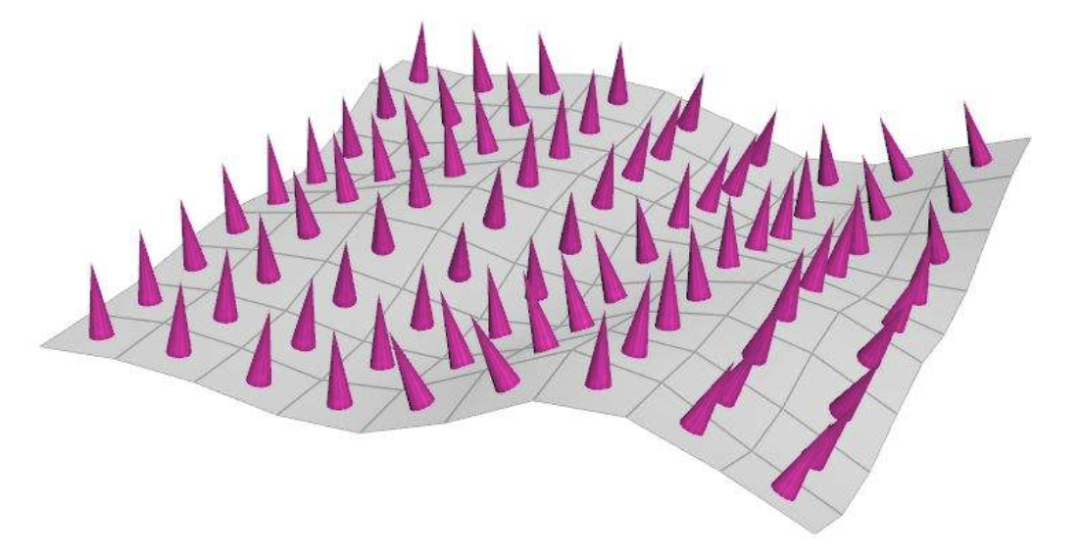
3D 模型中，每一个面，都可以用一个法线来表示朝向。如上图所示，紫色的圆锥指向的方向即为法线方向。

由于点乘的规律（夹角小于90度时为正，大于90度时为负）刚好符合判断机制，所以我们通常采用点乘进行一些正负向的判断。

由点乘规则可知：

• 当 dot(Plane,P) > 0 时，点在平面正面；

• 当 dot(Plane,P) = 0 时，点在平面上；

• 当 dot(Plane,P) < 0 时，点在平面背面。

双面材质

有了上面的关于平面的基础知识，双面材质的实现就非常易于理解了。

实现双面材质需要注意三点：

1、设置材质的 CullMode 为 None，如下图所示：

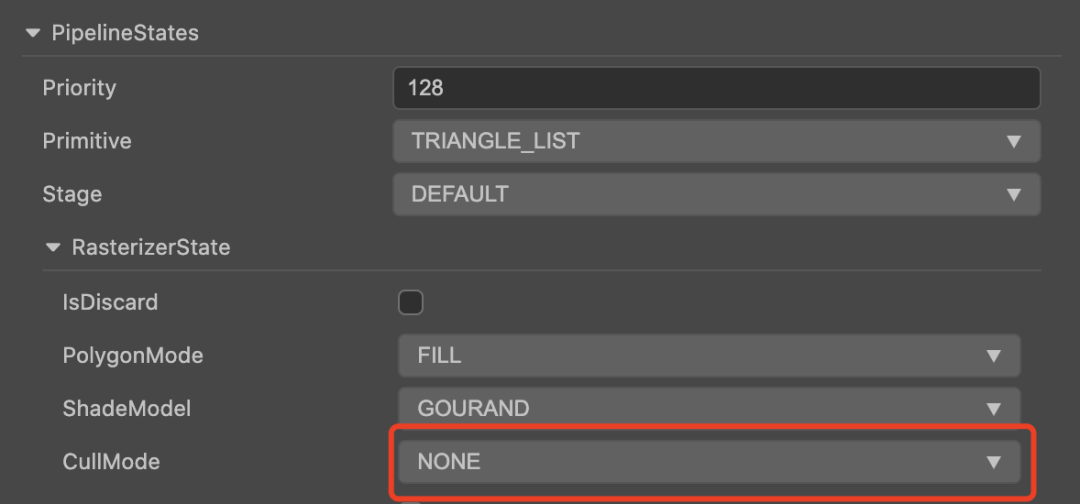
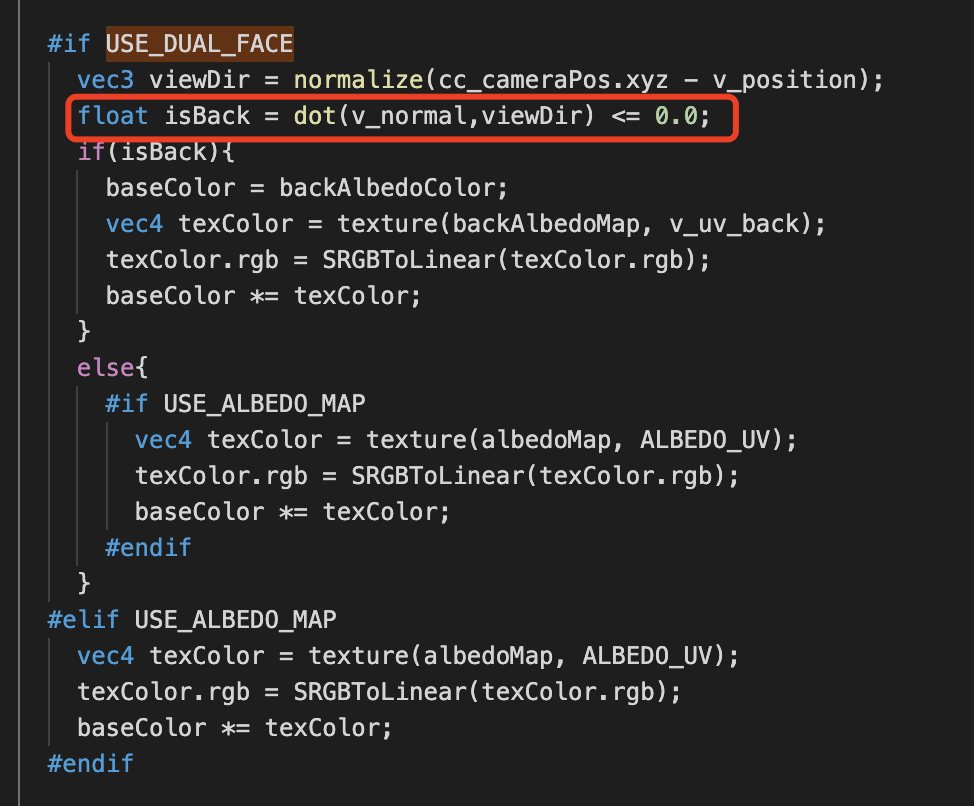
2、根据朝向判断采用正面还是背面的贴图和颜色

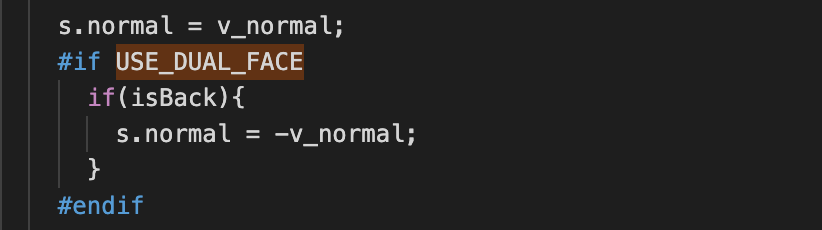
3、当为背面时，翻转法线，才能确保光照正确，如下图所示：

最终实现的效果如下：

应用场景

双面材质可以应用在一些需要双面显示且双面材质不同的地方，包括但不限于：

• 人物衣服、裙子、飘带里外

• 单向透光玻璃

• 阔叶植被（如芭蕉树、椰子树等）

• 布料、纸张等特殊展示场合

自定义裁剪面可以应用在一些需要剔除部分物体的地方，包括但不限于：

• 实时水面、镜面渲染

• 模型特效

• 因功能导致的特殊渲染需求

自定义裁剪面

自定义裁剪面算是平面最基础的应用，它的思路与背面剔除很接近：

1、在Shader自定义一个平面

在Shader中定义平面非常简单，只需两步：

• 在 properties 中添加一个 clipPlane 属性

• 在 uniform block 中声明一个 vec4 clipPlane。

2、剔除平面背后的内容

使用 dot 函数进行平面判定,若位置处于平面背后，则使用 discard 指令进行剔除，如下图所示：

为了更好地展示裁剪效果，麒麟子写了一个虚空飞龙入侵世界的 DEMO。

天空中出现了另一个时空与这个世界的连接口，龙群从虚空连接口陆续飞出并在连接口盘旋，效果如下所示：