学习笔记|SPSS|描述变量|按照3倍标准差剔除异常值|标准化值另存为变量|剔除个案|Zscore|箱图|Zscore取值范围

学习目的
软件版本
原始文档
概述
服从正态分布-按照3倍标准差剔除异常值
- 读数据
- 数据概览
- - 描述变量
- 正态性检验
- 异常值检验及剔除
非正态分布-根据Zscore取值范围确定
- 基础数据
- 数据概览
- - 正态性检验
  - Tips：箱图圆圈的含义
- 异常值检验及剔除
- - 描述变量，并将标准化值另存为变量：
  - 异常值筛选
Tips:Zscore取值范围
Tips：什么是Z-score?有哪些使用场景？

学习目的

SPSS按照3倍标准差剔除异常值

软件版本

IBM SPSS Statistics 26。

原始文档

spss按照3倍标准差剔除异常值
《小白爱上SPSS》课程第3讲数据

概述

数据需要服从正态分布。在3∂原则下，异常值如超过3倍标准差，那么可以将其视为异常值。正负3∂的概率是99.7%，那么距离平均值3∂之外的值出现的概率为P(|x-u| 3∂) = 0.003，属于极个别的小概率事件。
如果数据不服从正态分布，也可以用远离平均值的多少倍标准差来描述。即，使用Z-分数（Z-score）进行判断，计算每个数据的Z-分数。样本中每个数据 - 样本平均数，除以样本标准差，即可以计算每个数据的Z-分数。Z-score的值应该为【-3，+3】，超过该值的存在为异常值的可能，需要进一步判断。

服从正态分布-按照3倍标准差剔除异常值

三倍标准差法剔除异常值是一种经典的数据处理方法，指根据样本量和样本方差确定统计准则，将极端异常值（离群点）剔除，它是根据样本量和样本方差体现出来的分布统计学中的“三倍标准差”原则来处理数据异常值的方法。
三倍标准差剔除异常值涉及两个概念;根据总体样本方差的大小，让算出每个样本的“允许范围”;.将超出“允许范围”的异常值剔除出去。
其具体步骤是: 1、计算样本的标准差;2、确定样本的允许范围;3、如果有极端异常值，就剔除出来。
总体样本标准差的大小和离群点的定义有关，一般将样本标准差的三倍作为样本允许偏差范围，即若极端值（离群点）超出三倍标准差，则该数据被认为是异常值，可以被剔除。
异常值指的是在观测样本中，偏离于绝大部分样本分布的值。在连续型变量中，如果一个值与该变量的均值超过2倍标准差，我们一般就可以将之视为异常值。
由于样本中的离群点影响样本的方差，因此用三倍标准差的方法能有效地将极端值剔除，使样本方差更准确。
三倍标准差剔除异常值的优点是简单、快捷，可被广泛应用于分析数据，但也有不足之处。如果总体数据分布不同，样本标准差容易受到偏差;如果总体数据分布是非正态分布，由于样本数据分布更集中，因此很可能会误判离群点，这种情况下，可以考虑调整标准差的倍数，要求更大倍数以保证准确率。

读数据

GET FILE='E:\E盘备份\recent\小白爱上SPSS\小白数据\第三讲 正态分布.sav'.

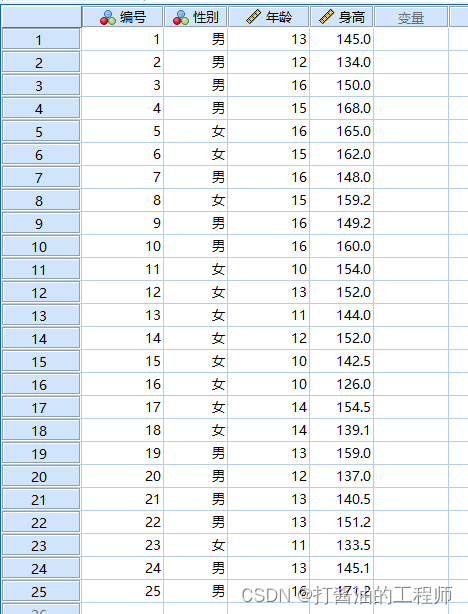
在这里插入图片描述

数据概览

描述变量

在这里插入图片描述
选择连续性变量“身高”作为描述变量，选择输出值类型：

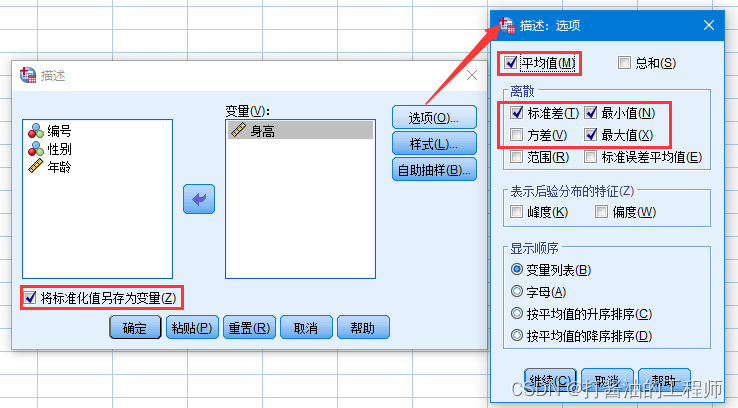
命令行：

DESCRIPTIVES VARIABLES=身高 /SAVE /STATISTICS=MEAN STDDEV MIN MAX	/*平均值，标准化值，最小值，最大值*/.

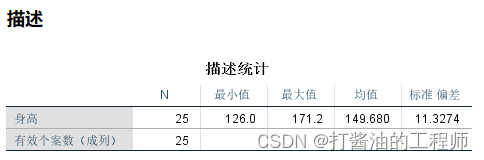
在这里插入图片描述

正态性检验

命令行：

EXAMINE VARIABLES=身高/PLOT HISTOGRAM NPPLOT /*若无此行，则不输出正态性检验表*//COMPARE GROUPS /STATISTICS DESCRIPTIVES /CINTERVAL 95 /MISSING LISTWISE /NOTOTAL.

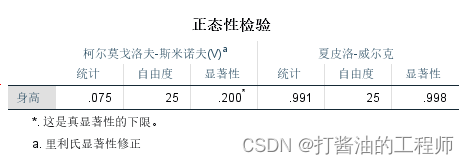
在这里插入图片描述
样本数量25个小于40个，使用夏皮洛-威尔克检验。经S-W检验，体重数据的P=0.998（P>0.05，接受原假设），没有统计学意义，可认为该组数据符合正态分布。
结合直方图：
命令行：

GRAPH 			/*绘图*//HISTOGRAM(NORMAL)=身高	/*直方图（正态）*/.

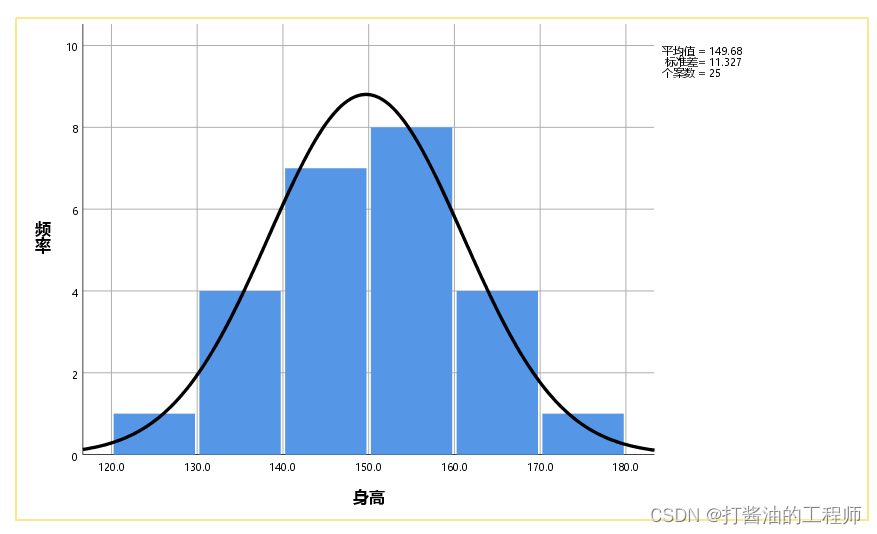
在这里插入图片描述
呈明显的倒钟型，该组数据符合正态分布。
身高的正态Q-Q图：

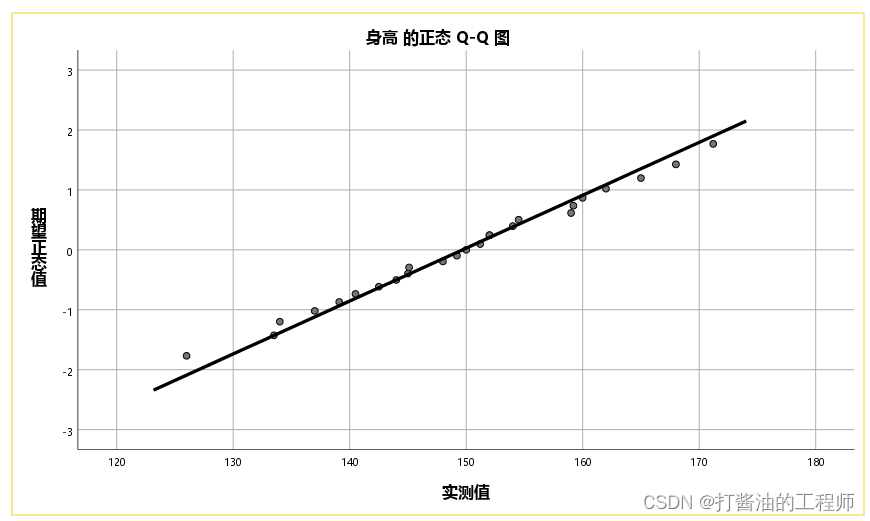
观察Q-Q图上的点能否分布在一条直线上，分布在一条直线上则说明近似或服从正态分布。
本例中，身高绝大多数的点能分布在一条直线上，直线趋势明显，可认为该连续数据服从正态分布。

异常值检验及剔除

数据-选择个案：
在这里插入图片描述
进入后，选择身高-选择如果条件满足：
筛选条件：身高 <= (149.68+311.3274) & 身高 >= (149.68-311.3274)

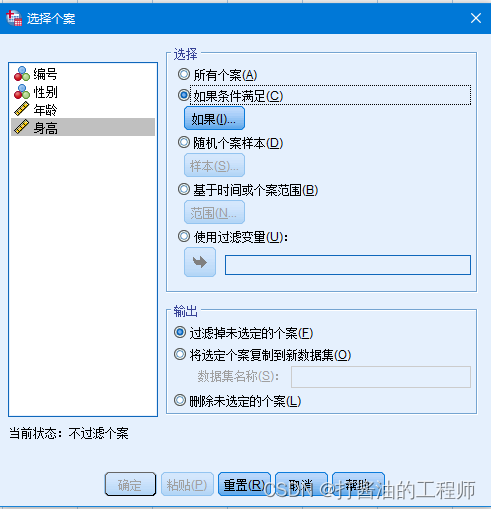
有效数据范围：

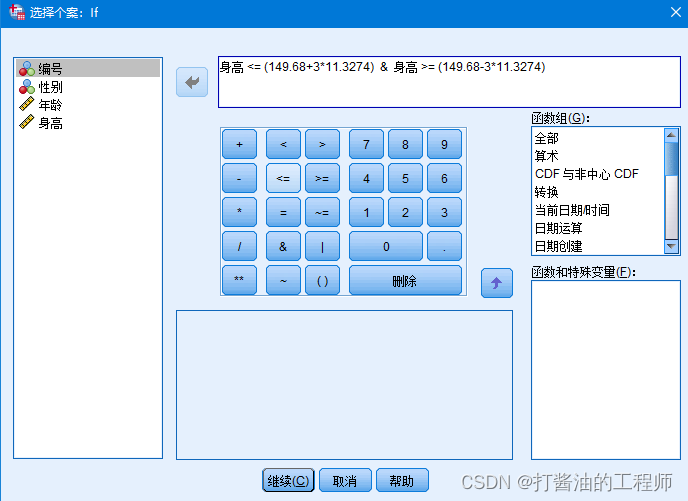
命令行：

USE ALL. 
COMPUTE filter_$=(身高 <= (149.68+3*11.3274)  &  身高 >= (149.68-3*11.3274)). 
VARIABLE LABELS filter_$ '身高 <= (149.68+3*11.3274)  &  身高 >= (149.68-3*11.3274) (FILTER)'. 
VALUE LABELS filter_$ 0 'Not Selected' 1 'Selected'. 
FORMATS filter_$ (f1.0). 
FILTER BY filter_$. 
EXECUTE.

数据均在平均值+/-33倍标准差范围内，无需剔除：
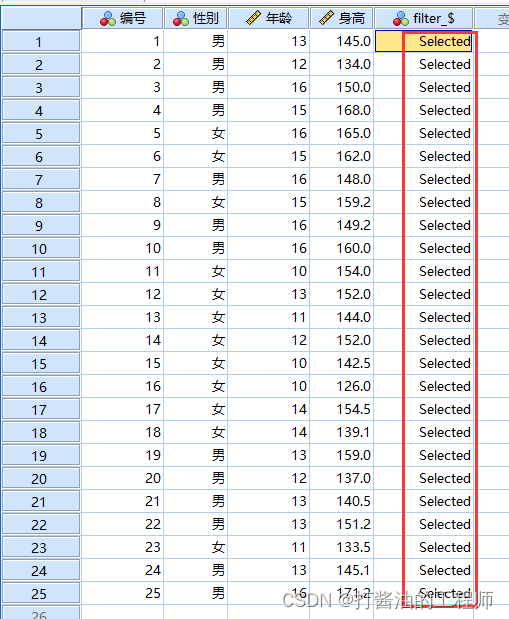
在这里插入图片描述

非正态分布-根据Zscore取值范围确定

基础数据

引自原文。
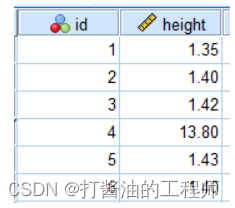
在这里插入图片描述

数据概览

正态性检验

命令行：

EXAMINE VARIABLES=height/PLOT BOXPLOT HISTOGRAM NPPLOT /*若无此行，则不输出正态性检验表，增加箱图输出：BOXPLOT*//COMPARE GROUPS /STATISTICS DESCRIPTIVES /CINTERVAL 95 /MISSING LISTWISE /NOTOTAL.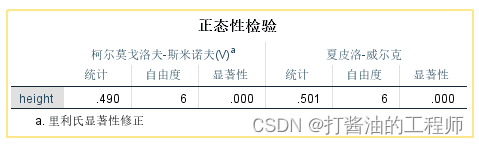

在这里插入图片描述
样本数量6个,小于40个，使用夏皮洛-威尔克检验。经S-W检验，体重数据的P<0.001（P<0.05，不接受原假设），有统计学意义，该组数据不符合正态分布。

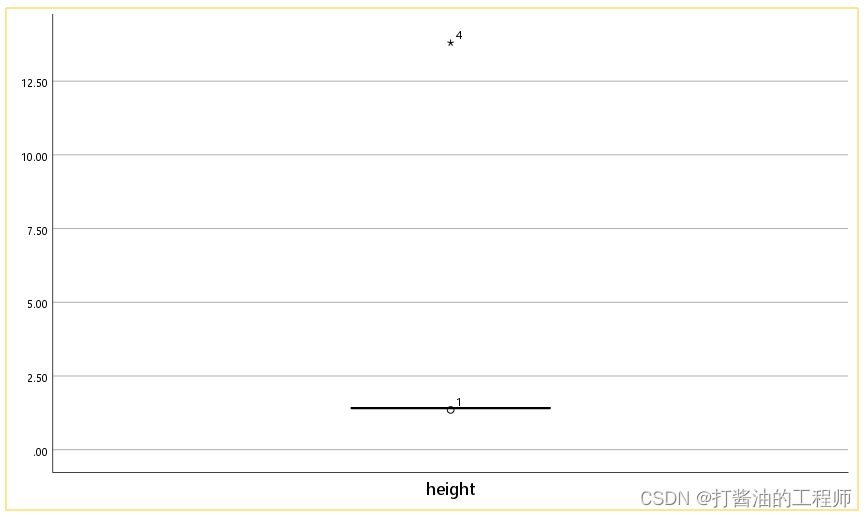
结合箱图，可以明显看到，id=4的数据明显偏离。

Tips：箱图圆圈的含义

箱线图中的“o"表示可疑的异常值﹐此处异常值的确定采用的是"五数概括法",即:变量值超过第75百分位点和25百分位点上变量值之差的1.5倍(箱体上方)或变量值小于第75百分位点和25百分位点上变量值之差的1.5倍(箱体下方)的点对应的值。

异常值检验及剔除

描述变量，并将标准化值另存为变量：

命令行：

DESCRIPTIVES VARIABLES=身高 /SAVE /STATISTICS=MEAN STDDEV MIN MAX	/*平均值，标准化值，最小值，最大值*/.

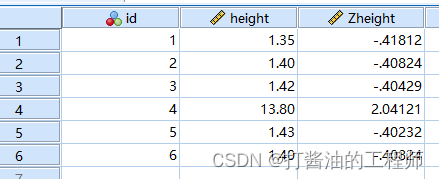
在这里插入图片描述

异常值筛选

说明：大多数指标均要求正常Z值区间为[-3,3]。Z值落在区间[-3,3]，我们所测值在总群体的发生概率为99.7%，超出这个区间的概率为0.3%。而本例中原作者采用的Z值区间标准较小小，如[-1.5，1.5]之间。
数据-选择个案：
进入后，选择Zscore-选择如果条件满足
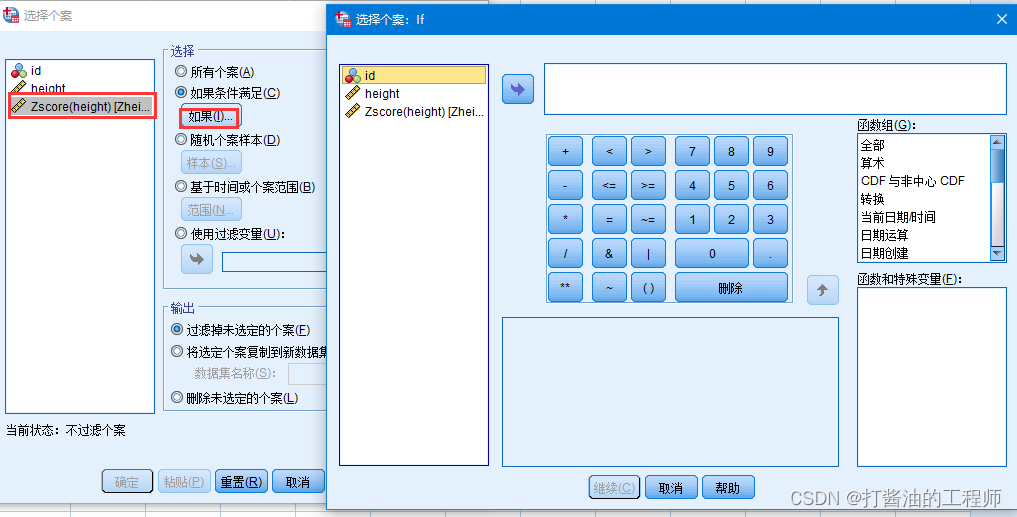
在这里插入图片描述
点击“如果”，输入条件，添加条件公式，使用变量名Z身高生成公式：
Zheight * 2 <= 3 & Zheight * 2 >=( -3 )

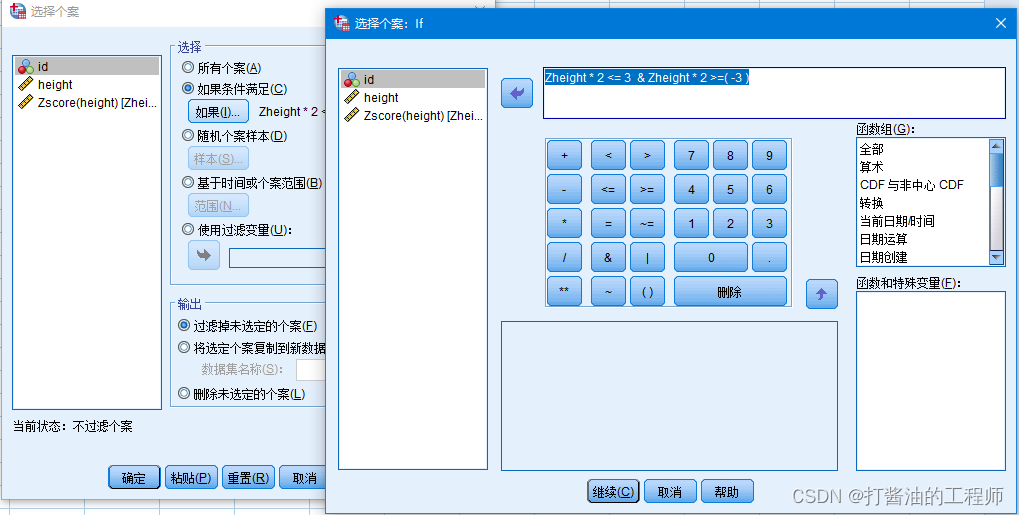
点击继续，确定，形成筛选列。

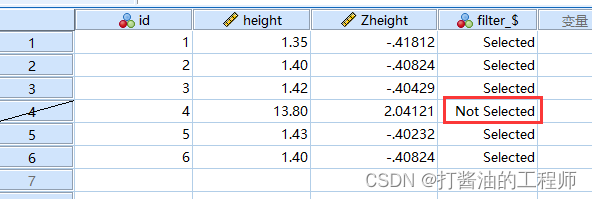
最终，下划线剔除id=4样本，filter变量Selected表示选中，Not Selected表示剔除。
命令行：

USE ALL. 
COMPUTE filter_$=(Zheight * 2 <= 3  & Zheight * 2 >=( -3 )). 
VARIABLE LABELS filter_$ 'Zheight * 2 <= 3  & Zheight * 2 >=( -3 ) (FILTER)'. 
VALUE LABELS filter_$ 0 'Not Selected' 1 'Selected'. 
FORMATS filter_$ (f1.0). 
FILTER BY filter_$. 
EXECUTE.

Tips:Zscore取值范围

引自百度文库：Zscore取值范围。
Z分数是一种常用的统计方法，用于度量一个数据点在数据集中的位置。它的取值范围为-3到+3之间，表示数据点与平均值的偏离程度和相对于标准差的偏离程度。Z分数的取值范围可以帮助我们解释和理解数据，判断异常值，以及进行比较和分析。无论在统计学还是其他领域，Z分数都具有重要的应用价值。
它衡量的是某个数据点与平均值的偏离程度，以及相对于标准差的偏离程度。Z分数可以告诉我们一个数据点相对于其他数据点的相对位置，从而帮助我们进行比较和分析。
Z分数的范围在理论上是无限的，但在实际应用中，我们通常将其限制在一定的取值范围内，以便更好地解释和理解数据。一般来说，Z分数的取值范围为-3到+3之间。超出这个范围的Z分数很少出现，因为它们表示的是极端的情况，即数据点与平均值的偏离程度非常大。
当Z分数为负数时，表示数据点低于平均值。例如，一个工分数为-2的数据点表示该数据点低于平均值两个标准差。当Z分数为正数时，表示数据点高于平均值。例如，一个7分数为+2的数据点表示该数据点高于平均值两个标准差。
Z分数的取值范围为-3到+3之间的原因是，根据正态分布的性质，约68%的数据点的Z分数在-1到+1之间，约95%的数据点的Z分数在-2到+2之间，约99.7%的数据点的Z分数在-3到+3之间。这个规律被称为“68-95-99.7法则”，它告诉我们在正态分布中，数据点相对于平均值的偏离程度大致符合这个分布。
Z分数的取值范围也可以用来判断数据的异常值。一般来说，Z分数超过3的数据点可以被认为是异常值，因为它们与平均值的偏离程度非常大。异常值可能是由于测量误差、数据录入错误或真实的异常情况导致的。通过识别和处理异常值，我们可以更准确地分析数据和做出决策。
除了在统计学中的应用，Z分数还被广泛应用于其他领域。例如，在金融领域中，Z分数可以用来度量股票的回报率相对于市场回报率的偏离程度，从而帮助投资者判断股票的表现。在医学研究中，Z分数可以用来比较不同患者群体的生物指标，帮助医生进行诊断和治疗决策。

Tips：什么是Z-score?有哪些使用场景？

引自：什么是Z-score?有哪些使用场景？
Z值（z-score，z-values, normal score）又称标准分数（standard score, standardized variable），是一个实测值与平均数的差再除以标准差的过程。Z score标准化是数据处理的一种常用方法。通过它能够将不同量级的数据转化为统一量度的Z score分值进行比较。
用公式表示为：
z=(x-μ)/σ
x为某实测值，μ为平均数，σ为标准差
Z值的量代表着实测值和总体平均值之间的距离，是以标准差为单位计算。
大于平均数的实测值会得到一个正数的Z值，小于平均数的实测值会得到一个负数的Z值。
一句话：
Z score通过（x-μ）/σ将两组或多组数据转化为无单位的Z score分值，使得数据标准统一化，提高了数据可比性，削弱了数据解释性。