卡特兰数问题

本文主要是介绍卡特兰数问题，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

链接

卡特兰数 - http://lanqi.org/skills/10939/

数值

C0 = 1,         
C1 = 1,         C2 = 2,          C3 = 5,          C4 = 14,          C5 = 42,
C6 = 132,       C7 = 429,        C8 = 1430,       C9 = 4862,        C10 = 16796,
C11 = 58786,    C12 = 208012,    C13 = 742900,    C14 = 2674440,    C15 = 9694845,
C16 = 35357670, C17 = 129644790, C18 = 477638700, C19 = 1767263190, C20 = 6564120420, ...

公式

通项公式一： $C_n = \frac{1}{n+1}C_{2n}^n=C_{2n}^n-C_{2n}^{n-1}=C_{2n}^n-C_{2n}^{n+1}$
通项公式二： $C_n = \frac{1}{n+1}\sum_{i=0}^n\left(C_{n}^i\right)^2$
递推公式一： $C_{n+1} = \frac{2(2n+1)}{n+2}C_n$
递推公式二： $C_{n+1} = C_0\times C_n+C_1\times C_{n-1}+…+C_{n-1}\times C_1+C_n\times C_0$
增长速度： $\Delta C_n \sim \frac{4^n}{n^{\frac{3}{2}}\times\sqrt{\pi}}$

通项公式一

设由n+1个 -1 和 n-1个 +1 (或者：n+1个 +1 和 n-1个 -1 )组成长度为2n的序列A。所有的可能数量a₁
$a_1=\frac{(2n)!}{(n+1)!\times(n-1)!}$
设由n个 +1 和 n个 -1 组成长度为2n的序列B。序列B若满足“前任意项的和不小于0”，则称该序列为合法序列，否则称非法序列。
- 所有非法的序列可能数量b₁
  $b_1 = a_1=\frac{(2n)!}{(n+1)!\times(n-1)!}$
- 所有合法的序列可能数量b₂
  $b_2=\frac{(2n)!}{n!\times n!} - b_1 = \frac{1}{n+1} \times \frac{(2n)!}{n!\times n!} = \frac{1}{n+1} \times C(2n, n)$
为什么 b₁ = a₁ ？
- 对A序列和非法B序列，前若干项和第一次小于0的位置只能是1、3、5、……、2n-1
- 根据第一次小于0位置对A序列、非法的B序列进行分类，都可以分为n类
- 前若干项和第一次小于0时，此时的和一定等于 -1
- 对于A序列，在2k+1位置第一次和小于0
  $\underbrace{1，……，-1}_{k个\pm1}，-1，\underbrace{……}_{n-k-1个+1，n-k个-1}$
- 对于非法B序列，在2k+1位置第一次和小于0
  $\underbrace{1，……，-1}_{k个\pm1}，-1，\underbrace{……}_{n-k个+1，n-k-1个-1}$
- 结论：在2k+1位置第一次和小于0，对应的可能数量相等。因此b₁ = a₁ 成立

递推公式二

对于合法B序列，前若干项和第一次等于0的位置只能是 2，4，6，……，2n
根据第一次等于0的位置对合法B序列进行分类，都可以分为n类
分类后，每类由两个子问题构成；例如：在2k位置第一次和等于0
$\overbrace{1，\underbrace{1，……，-1}_{k-1个\pm1}，-1}^{k个\pm1}，\underbrace{1，……，-1}_{n-k个\pm1}$
对应的排列数：
$C_{k-1} \times C_{n-k}$
所以，总的排列数
$C_n = C_0\times C_{n-1}+C_1\times C_{n-2}+C_2\times C_{n-3}+…+C_{n-1}\times C_0$

例题

一个足够大的栈的进栈序列为1,2,3,…,n时有多少个不同的出栈序列？

圆周上有2n个点，以这些点为端点连互不相交的n条弦，求不同的连法总数.

在这里插入图片描述

有n个结点，问总共能构成几种不同的二叉树.
如中序遍历，根结点第k个被访问到，则根结点的左子树有k-1个点、根结点的右子树有n-k个点。k的取值范围为1到n。【2015年腾讯实习生在线笔试题】

一个凸的n边形，用直线连接它的两个顶点使之分成多个三角形，每条直线不能相交，问一共有多少种划分方案。

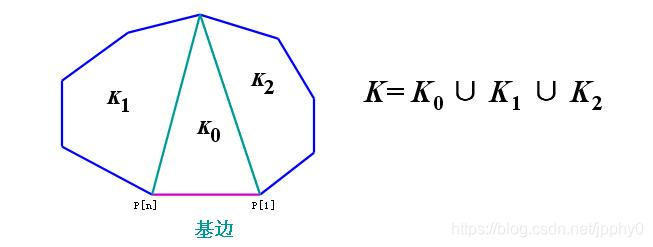
有n+1个叶子的满二叉树的个数？

向左记为+1，向右记为-1，按照向左优先的原则，从根节点开始遍历．例如第一个图记为+1,+1,+1,−1,−1,−1。【即符合卡特兰数的含义】

在n*n的格子中，只在下三角行走，每次横或竖走一格，有多少中走法？
向右相当于进栈，向左相当于出栈。（这个模型是进出栈问题的一个几何解释）

由n对括号形成的合法括号表达式的个数。
- 当n=3时，合法的表达式共有:((())),(())(),()(()),()()(),(()())，共5个。
- 表达式和指针结合可以视作乘法操作指令。指针：指向操作数，初始时刻，指针指向第一个数；左括号：指针右移一格；右括号：将指针当前指向的数与其左侧的一个数作乘积，并删除左侧的那个数。
- 如图所示，1,2,3,4相乘时取n=3，当执行完括号表达式，就得到了一种可能的相乘顺序．