2018宁夏acm网络赛-G-Trouble of Tyrant-斜率优化-决策单调性

（有任何问题欢迎留言或私聊 && 欢迎交流讨论哦

题目：传送门

思路：

 非常明显要用到斜率优化这一技巧。

(显然为了方便，要将点从新逆序编号)
ar[i]表示从1经过i条边到达点n，所经过的路径长度。
dp[i]表示每条边增加长度d后，新的ar[i]值。

第一步：

假设i > j 且ar[i] < ar[j]，如果边增加长度d后，在点 i 的决策劣于在点 j 的决策，则：

dp[i]=ar[i]+id dp[j]=ar[j]+jd 且 dp[i] > dp[j]

=> ar[i]-ar[j] >= d*(j-i)

=> (ar[i]-ar[j])/(i-j) >= -d

将上述式子定义为i和j的斜率。注意：j < i。
 如果在点 i 处决策劣于在点 j 处决策，则有：斜率(j, i) >= -d

(ar[i]-ar[j])/(i-j) >= -d

第二步：

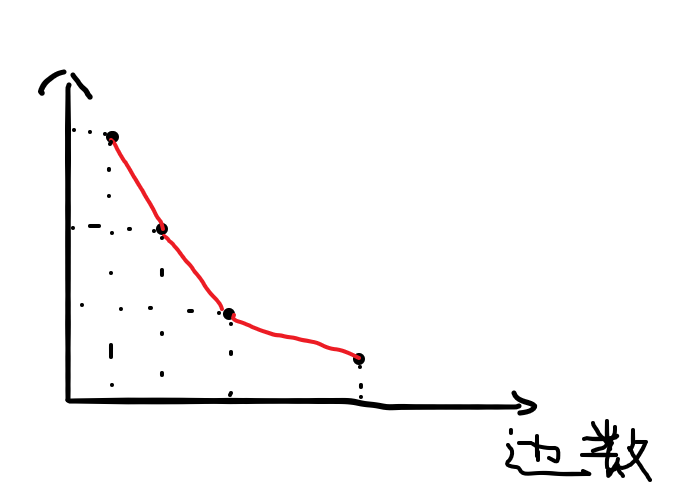
所以我们就利用单调队列构造一个斜率上升的凸包，注意斜率是负的。大概长这个样子：

因为构造出来的是斜率变大的下凸包，它的决策单调性的优度是递减的。
为了保证计算每个 d 的答案正确。
我选择把d从小到大排序，这样 -d 就是从大到小排序。
最后从构造出来的凸包末尾开始依次计算排序后的 -d 的值。

从开头还是从末尾开始计算不同d值下的最短路径，是差不多的，改一下细节就可以了，两种方法我都过了这题。(从开头开始计算要快一点点)

具体看代码实现。

结构体c数组储存路径的长度及边数。
结构体op数组储存d值
结构体数组que为队列

AC代码

/*
**链接**
传送门: [here](https://nanti.jisuanke.com/t/A1670)
**题意**
$N,K 1e5$
无向图，n个节点，2n-3条边。n-1条边从1->i .(2<=i<=n)。n-2条边从i->i+1.(2<=i<=n-1)k次询问，问将每条边长度增加d后，从1到n的最短路径。
**思路**
[2018宁夏acm网络赛-G-Trouble of Tyrant](https://blog.csdn.net/qq_39599067/article/details/80671353)
类似题：[BZOJ1010](https://blog.csdn.net/qq_39599067/article/details/80668515)
**备注**
*/
const int MXN = 2e6 + 5;
const int MXE = 2e6 + 6;int n, m;
int64 dp[MXN], ar[MXN], sum[MXN], id[MXN], qry[MXN], ans[MXN];
int Q[MXN], hd, tl;
void read_data() {n = read(), m = read();for(int i = n - 1; i >= 1; --i) ar[i] = read();for(int i = n - 1; i >= 2; --i) sum[i] = read();for(int i = 2; i < n; ++i) sum[i] += sum[i - 1];for(int i = 1; i < n; ++i) ar[i] += sum[i];for(int i = 1; i <= m; ++i) {id[i] = i;qry[i] = read();}
}
int64 KX(int j, int k) {return ar[k] - ar[j];
}
int64 KY(int j, int k) {return k - j;
}
bool cmp1(const int &a, const int &b) {return qry[a] < qry[b];
}
bool cmp2(const int &a, const int &b) {return qry[a] > qry[b];
}
void gao_solve() {sort(id + 1, id + m + 1, cmp1);hd = tl = 0;for(int i = 1; i < n; ++i) {if(tl > hd && ar[i] >= ar[Q[tl - 1]]) continue;while(tl - hd >= 2 && KX(Q[tl-2], Q[tl-1]) * KY(Q[tl-1], i) >= KX(Q[tl-1], i) * KY(Q[tl-2], Q[tl-1])) -- tl;Q[tl++] = i;}for(int i = 1; i <= m; ++i) {while(tl - hd >= 2 && KX(Q[tl - 2], Q[tl - 1]) >= KY(Q[tl - 2], Q[tl - 1]) * (-qry[id[i]])) -- tl;ans[id[i]] = ar[Q[tl - 1]] + Q[tl - 1] * qry[id[i]];}
}
void print_ans() {for(int i = 1; i <= m; ++i) printf("%lld%c", ans[i], " \n"[i==m]);
}
int main() {
#ifdef LH_LOCALfreopen("D:in.in", "r", stdin);freopen("D:out.out", "w", stdout);
#endifint tim = read();while(tim --) {read_data();gao_solve();print_ans();}
#ifdef LH_LOCAL// cout << "time cost:" << 1.0 * clock() / CLOCKS_PER_SEC << "s" << endl;// system("pause");
#endifreturn 0;
}

#include<bits/stdc++.h>
#define fang(a) (a)*(a)
using namespace std;
typedef long long LL;
const int N = 100000+7;
int n,k,head,tail;
LL ar[N],f[N],d[N];
struct lp{int id;LL v;
}op[N],c[N],que[N];
bool cmp1(lp &a,lp &b){return a.v>b.v;
}
bool cmp2(lp &a,lp &b){return a.v<b.v;
}
/*
i>j
dp[i]=ar[i]+i*k
dp[j]=ar[j]+j*k
dp[i] >= dp[j]
ar[i]-ar[j] >= k*(j-i)
(ar[i]-ar[j])/(i-j) >= -k
维持一个斜率单调上升的队列（斜率是负的）
把k从小到大排序，则-k从大到小排序
从队列末尾开始匹配-k
*/
bool cd(lp a,lp b,lp c){return ((b.id-a.id)*(c.v-a.v)-(b.v-a.v)*(c.id-a.id))<0;
}
double fx(lp x,lp y){return (y.v-x.v*1.0)/(y.id-x.id);
}
int main(){int tim;scanf("%d",&tim);while(tim--){scanf("%d%d",&n,&k);/***********************/for(int i=n-1;i>=1;--i){scanf("%lld",&ar[i]);}for(int i=n-1;i>=2;--i){scanf("%lld",&d[i]);}for(int i=3;i<=n-1;++i){d[i]+=d[i-1];}for(int i=2;i<=n-1;++i){ar[i]+=d[i];}for(int i=1;i<=n-1;++i){c[i].id=i;c[i].v=ar[i];}/*以上是处理路径的长度和边数的代码*/for(int i=0;i<k;++i){scanf("%lld",&op[i].v);op[i].id=i;}sort(op,op+k,cmp2);for(int i=1;i<=n-1;++i){//printf("%d %lld\n",c[i].id,c[i].v );}head=tail=1;memset(f,0,sizeof(f));for(int i=1;i<=n-1;++i){//构造凸包if(head<tail&&c[i].v>=que[tail].v)continue;//这个新点代表的路径长度大于或等于上一个点且边数较多，则可以pass掉，画个图理解下吧while(head<tail-1&&cd(que[tail-1],que[tail],c[i]))tail--;que[++tail]=c[i];}//printf("*%d\n",tail );for(int i=0;i<k;++i){//按照上面红色的式子计算最优值while(head<tail-1&&fx(que[tail-1],que[tail])>=-op[i].v)tail--;f[op[i].id]=que[tail].v+que[tail].id*op[i].v;}for(int i=0;i<k;++i){printf(i!=k-1?"%lld ":"%lld\n",f[i] );}}return 0;
}

数据很水，错的代码都能ac
比如数据：
3 3
1 3
4
0 2 4
应该输出：
3 5 7

#include<bits/stdc++.h>
#define fang(a) (a)*(a)
using namespace std;
typedef long long LL;
const int N = 100000+7;
int n,k,head,tail;
LL ar[N],f[N],d[N];
struct lp{int id;LL v;
}op[N],c[N],que[N];
bool cmp1(lp &a,lp &b){return a.v>b.v;
}
bool cmp2(lp &a,lp &b){return a.v<b.v;
}
/*
i>j
dp[i]=ar[i]+i*k
dp[j]=ar[j]+j*k
dp[i] >= dp[j]
ar[i]-ar[j] >= k*(j-i)
(ar[i]-ar[j])/(i-j) >= -k
维持一个斜率单调上升的队列（斜率是负的）
把k从小到大排序，则-k从大到小排序
从队列末尾开始匹配-k
*/
bool cd(lp a,lp b,lp c){return ((b.id-a.id)*(c.v-a.v)-(b.v-a.v)*(c.id-a.id))<0;
}
double fx(lp x,lp y){return (y.v-x.v*1.0)/(y.id-x.id);
}
int main(){int tim;scanf("%d",&tim);while(tim--){scanf("%d%d",&n,&k);/***********************/for(int i=n-1;i>=1;--i){scanf("%lld",&ar[i]);}for(int i=n-1;i>=2;--i){scanf("%lld",&d[i]);}for(int i=3;i<=n-1;++i){d[i]+=d[i-1];}for(int i=2;i<=n-1;++i){ar[i]+=d[i];}for(int i=1;i<=n-1;++i){c[i].id=i;c[i].v=ar[i];}/*以上是处理路径的长度和边数的代码*/for(int i=0;i<k;++i){scanf("%lld",&op[i].v);op[i].id=i;}sort(c+1,c+n,cmp1);sort(op,op+k,cmp2);for(int i=1;i<=n-1;++i){//printf("%d %lld\n",c[i].id,c[i].v );}head=tail=1;memset(f,0,sizeof(f));for(int i=1;i<=n-1;++i){//构造凸包if(head<tail&&c[i].id<=que[tail].id)continue;//这个新点代表的路径长度小于或等于上一个点且边数较少，则可以pass掉，画个图理解下吧while(head<tail-1&&cd(que[tail-1],que[tail],c[i]))tail--;que[++tail]=c[i];}//printf("*%d\n",tail );for(int i=0;i<k;++i){//按照上面红色的式子计算最优值while(head<tail-1&&fx(que[tail-1],que[tail])>=-op[i].v)tail--;f[op[i].id]=que[tail].v+que[tail].id*op[i].v;}for(int i=0;i<k;++i){printf(i!=k-1?"%lld ":"%lld\n",f[i] );}}return 0;
}

Tyrant has a private island on the Pacific Ocean. He has built many luxury villas on the island. He flies here every vacation to enjoy life. He will drive his sports car between his villas. Tyrant has n villas on the island and the last villa which is numbered by n is his favorite. His money is only allowed to build one airpor located at the first villa which is numbered by 1 so every time he come to the island, he will land at the villa numbered 1. What’s more Tyrant build 2*n-3 roads on the island. For every villa except the first island, there is a two-way street connecting this villa and the first villa. For every villa numbered by i (i >= 3) there is a two-way street connecting this villa and the villa numbered by i - 1. Tyrant is not satisfied, he think the road is not long enough. He asks q problems, every problem has a non negative integer d. He want to know if the length of each road is increaced by d what is the shortest distance between the first villa and his favorite villa. Notice that the increment in each problem is not cumulative – in other words it doesn’t take effect on the real road after query.

Input:

The first integer indicate the number of test cases T (T <= 10).

In each test cases the first line contains two integers n and q – the number of villas and the number of queries (3 <= n <= 100000, 1 <= q <= 100000).

The second line contains n - 1 non-negative integers – ai describe a road with length ai connecting villa 1 and i (2 <= i <= n)

The third line contains n - 2 non-negative integers – bi describe a road with length bi connecting villa i - 1 and i (3 <= i <= n)

The next line contains q non-negative integers – di means Tyrant want to know what is the shortest distance between the first villa ans his favorite villa when the length of each road is increaced by di.

All integers are 32-bit signed integer.

Output:

For each test case you should output q integers in one line means the answer for each problem.

样例输入
1
3 3
1 5
2
0 2 4
样例输出
3 7 9