基于Matlab的策动点阻抗快速综合库函数-微带线综合

2023-11-06 18:01
文章标签 matlab 综合 快速 库函数 阻抗 策动 微带线

本文主要是介绍基于Matlab的策动点阻抗快速综合库函数-微带线综合，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

基于Matlab的策动点阻抗快速综合库函数-微带线综合

参考书籍：
MICROWAVE AMPLIFIER AND ACTIVE CIRCUIT DESIGN USING THE REAL FREQUENCY TECHNIQUE

1、环境安装

下载RFPLSynth包，链接：https://github.com/Grant-Giesbrecht/RFPLSynth。在下载得到的文件中打开install.m文件并运行：
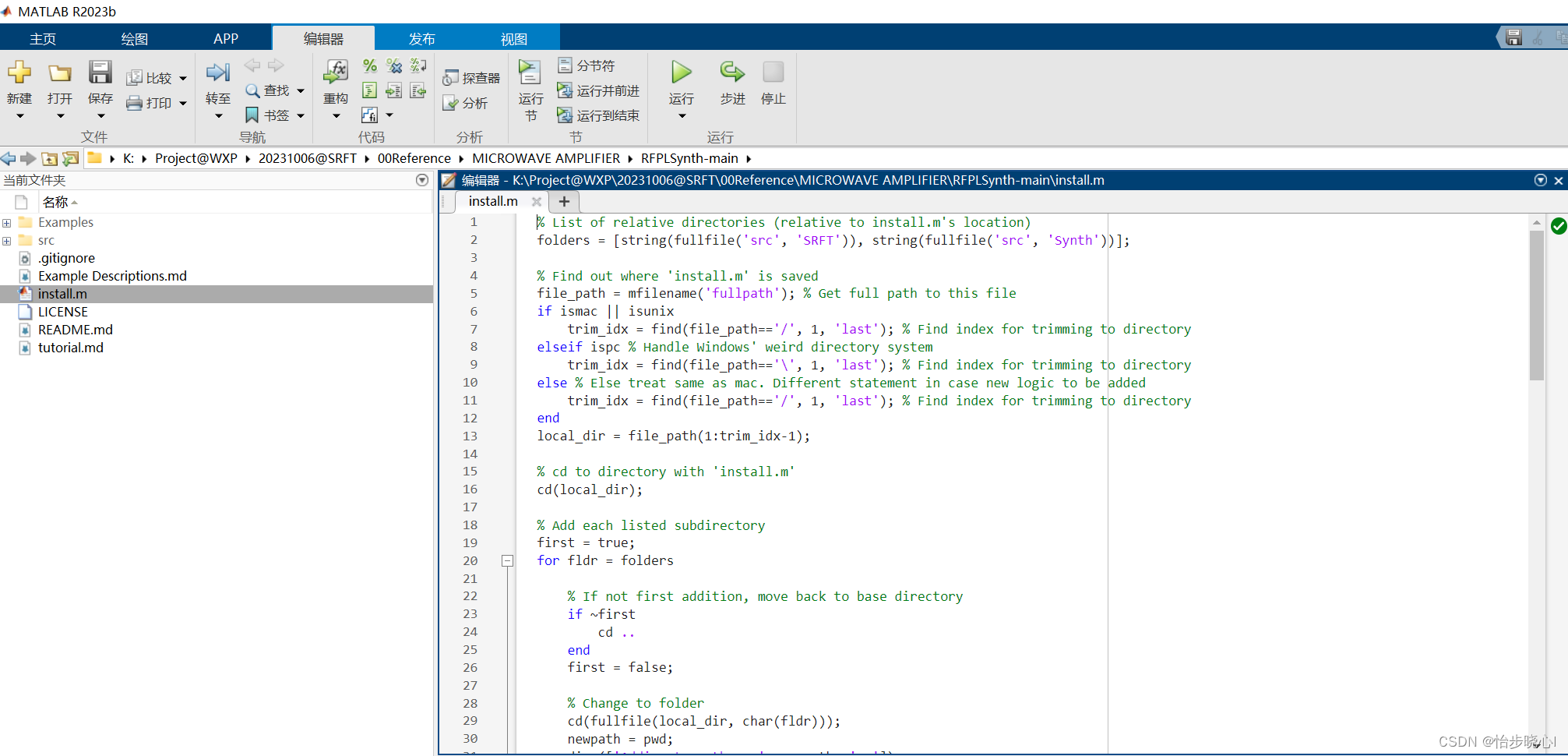
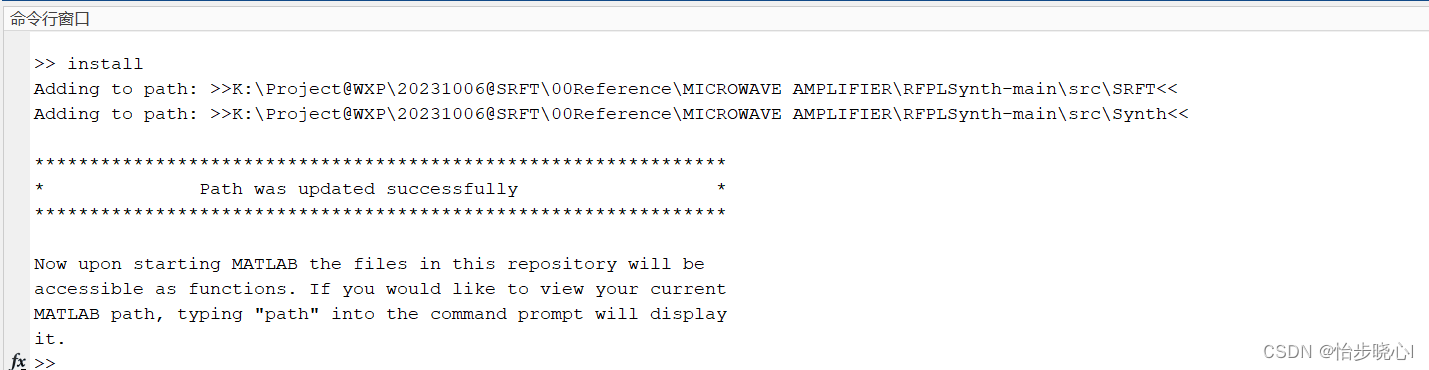
在这里插入图片描述
如果运行得到如下安装成功的结果，则安装完成：
在这里插入图片描述

这个包需要安装MSTD的Matlab依赖包，链接：
https://github.com/Grant-Giesbrecht/MSTD/tree/main
这个包可以帮助进行简单日常计算的 MATLAB 函数。许多（但不是全部）函数都侧重于基本电路方程和数据导入或处理。
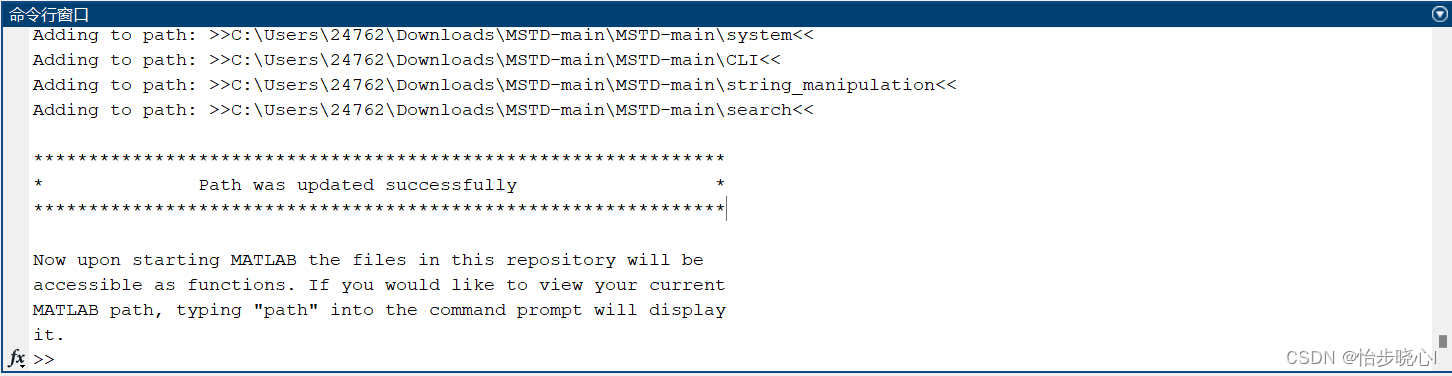
同样在下载的文件中找到install.m文件并运行在这里插入图片描述
如果运行得到如下安装成功的结果，则安装完成：
在这里插入图片描述
此外，RFPLSynth包中的Netlist文件的四百多行存在一些错误需要改正：
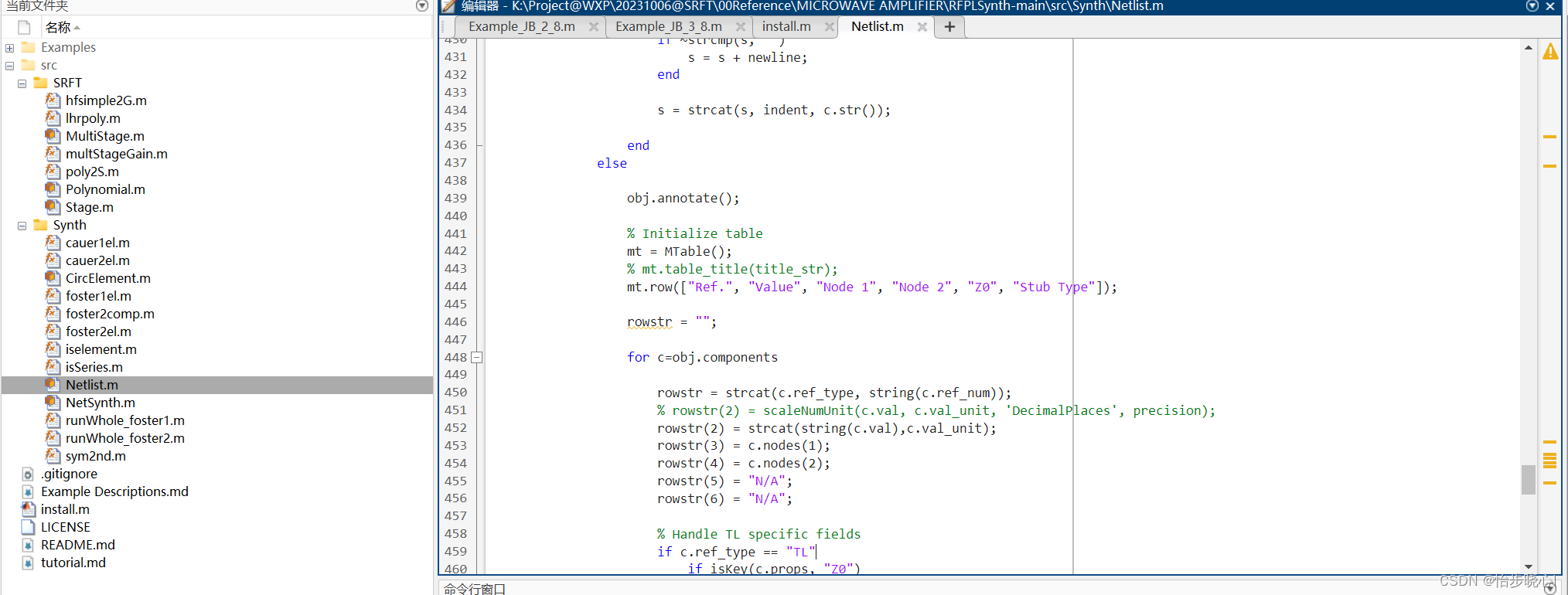
在这里插入图片描述
使用如下的代码进行部分替换即可，不然运行会报错（mt.table_title没有定义这个方法，且scaleNumUnit找不到这个函数）：

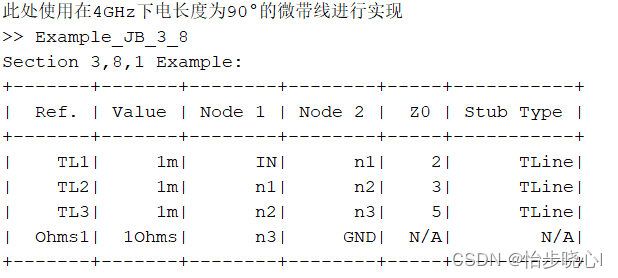
% Initialize tablemt = MTable();% mt.table_title(title_str);mt.row(["Ref.", "Value", "Node 1", "Node 2", "Z0", "Stub Type"]);rowstr = "";for c=obj.componentsrowstr = strcat(c.ref_type, string(c.ref_num));% rowstr(2) = scaleNumUnit(c.val, c.val_unit, 'DecimalPlaces', precision);rowstr(2) = strcat(string(c.val),c.val_unit);rowstr(3) = c.nodes(1);rowstr(4) = c.nodes(2);rowstr(5) = "N/A";rowstr(6) = "N/A";

2、微带线综合

%=========================================================================%
% This example shows how to use Richard's extraction to realize a
% distributed element circuit from an impedance function. The impedance
% function must be in terms of te Richard's variable (t = j*Z0*tan(theta))
% rather than the laplace variable 's'. This example demonstrates circuits
% with both stubs and stepped impedance lines. This example replicates the
% example in Section 3,8,1 and 3,8,2 of "Microwave Amplifier and Active
% Circuit Design Using the Real Frequency Technique" by P. Jarry & J.
% Beneat.
%
% PROBLEM DESCRIPTION:
% Design a distributed element circuit realizing the input impedance
% functions:
%    1.         100*t^3 + 50*t^2 + 300*t + 30
%		Z(t) = -------------------------------	(Section 3,8,1 Ex.)
%                9*t^3 + 170*t^2 + 31*t + 30
%
%    2.               18*t^2 + 240*t + 30
%		Z(t) = -------------------------------	(Section 3,8,2 Ex.)
%                9*t^3 + 170*t^2 + 31*t + 30
%
% such that 't' is the Richard's variable.
%
% 
% Author: G. Giesbrecht
% Contact: grant.giesbrecht@colorado.edu
%
%=========================================================================%% Define polynomial vectors
num_1 = [100, 50, 300, 30];
num_2 = [18, 240, 30];den = [9, 170, 31, 30];% Example from J+B Section 3,8,1
synth_1 = NetSynth(num_1, den);
synth_1.generate("Richard");% Example from J+B Section 3,8,2
synth_2 = NetSynth(num_2, den);
synth_2.generate("Richard");% Print Results
displ("Section 3,8,1 Example:");
displ(synth_1.circ.str());displ(newline, "Section 3,8,2 Example:");
displ(synth_2.circ.str());% 使用4GHZ的微带线，最高控制到4GHz，特性阻抗1欧姆
f=4e9;
fe=4e9;we=2*pi*fe;
tau=pi/2/we;
%光速
c=299792458;
ele_l=360*tau*f;
l=ele_l/360*c/f;
disp(['此处使用在',num2str(f/1e9),'GHz下电长度为',num2str(ele_l),'°的微带线进行实现']);%求解频率范围，单位GHz
f_start=0.1;
f_stop=4;
f_step=0.1;
%求解范围
freq_solve=[f_start:f_step:f_stop]*1e9;
%计算不同频率下的相移常数beta
beta=2*pi*freq_solve/c;
%转换到lamda域
lamda=1j*tan(beta*l);%    1.         100*t^3 + 50*t^2 + 300*t + 30
%		Z(t) = -------------------------------	(Section 3,8,1 Ex.)
%                9*t^3 + 170*t^2 + 31*t + 30
num_num1=0;
for i=1:1:length(num_1)num_num1=num_num1+num_1(i).*lamda.^(length(num_1)-i);
end
num_den=0;
for i=1:1:length(den)num_den=num_den+den(i).*lamda.^(length(den)-i);
end
Zin=num_num1./num_den;
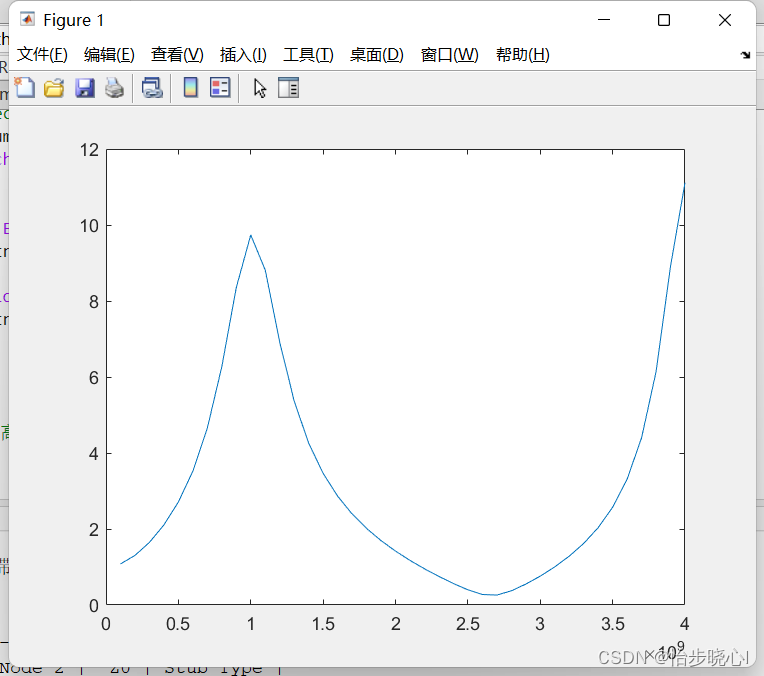
figure
plot(freq_solve,abs(Zin))%    2.               18*t^2 + 240*t + 30
%		Z(t) = -------------------------------	(Section 3,8,2 Ex.)
%                9*t^3 + 170*t^2 + 31*t + 30
num_num1=0;
for i=1:1:length(num_2)num_num1=num_num1+num_2(i).*lamda.^(length(num_2)-i);
end
Zin=num_num1./num_den;
figure
plot(freq_solve,abs(Zin))

第一个案例的结果：
在这里插入图片描述
Matlab的Zin结果：
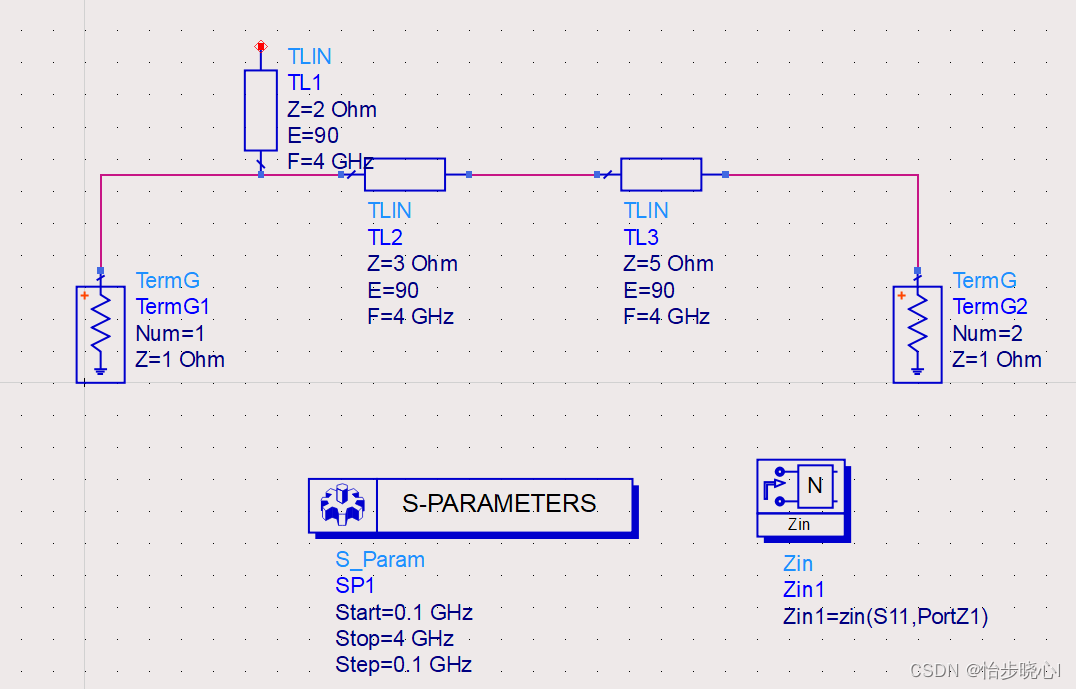
在这里插入图片描述
ADS结构：
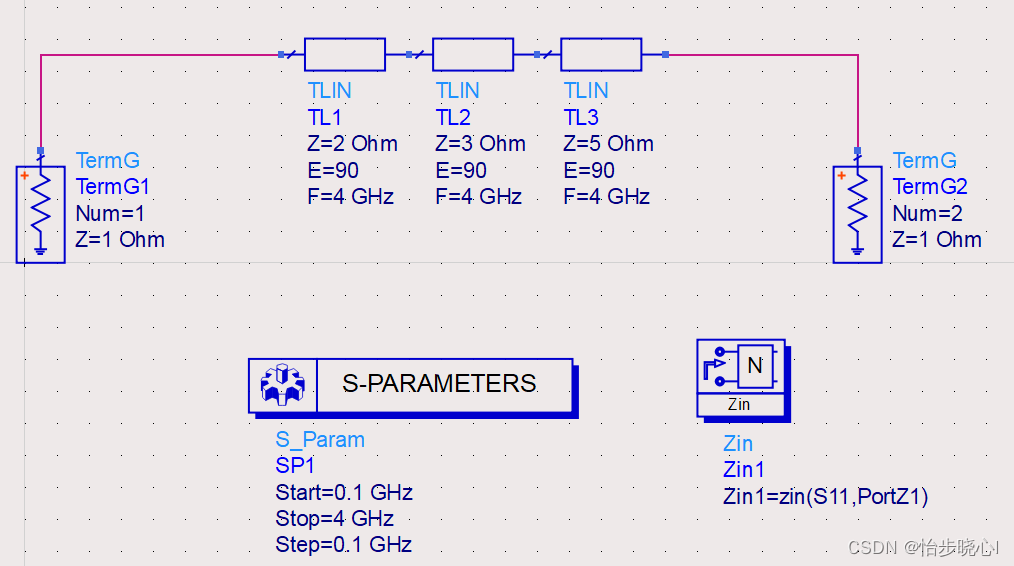
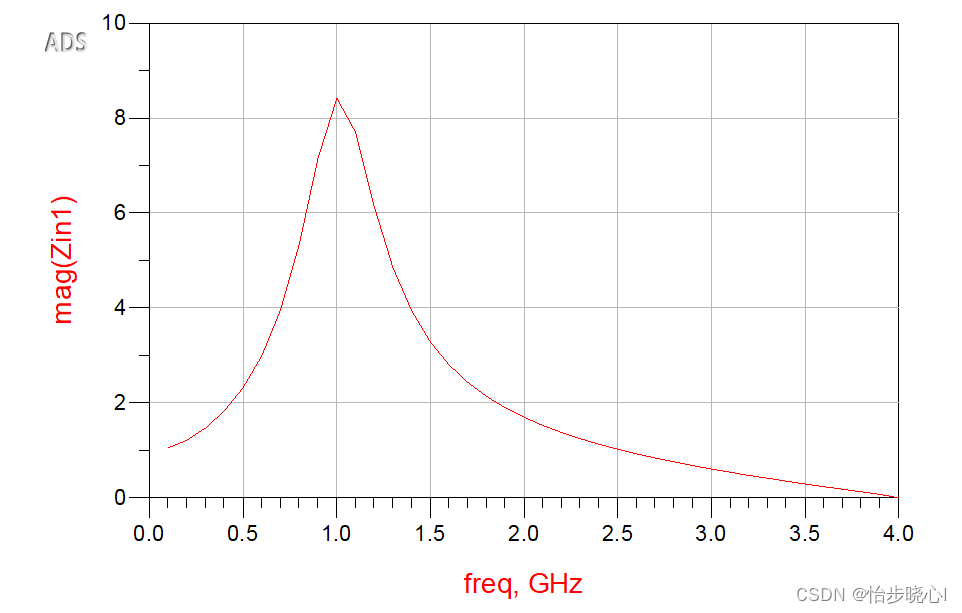
在这里插入图片描述
ADS的Zin结果：
在这里插入图片描述
第二个案例的结果：
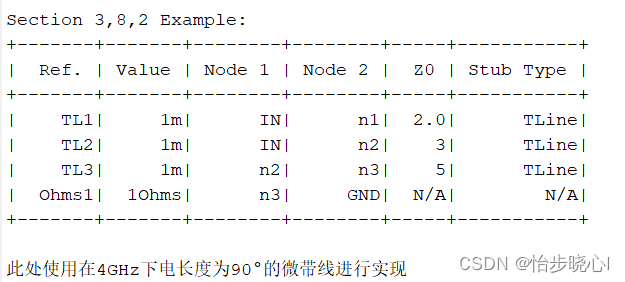
在这里插入图片描述
Matlab的Zin结果：
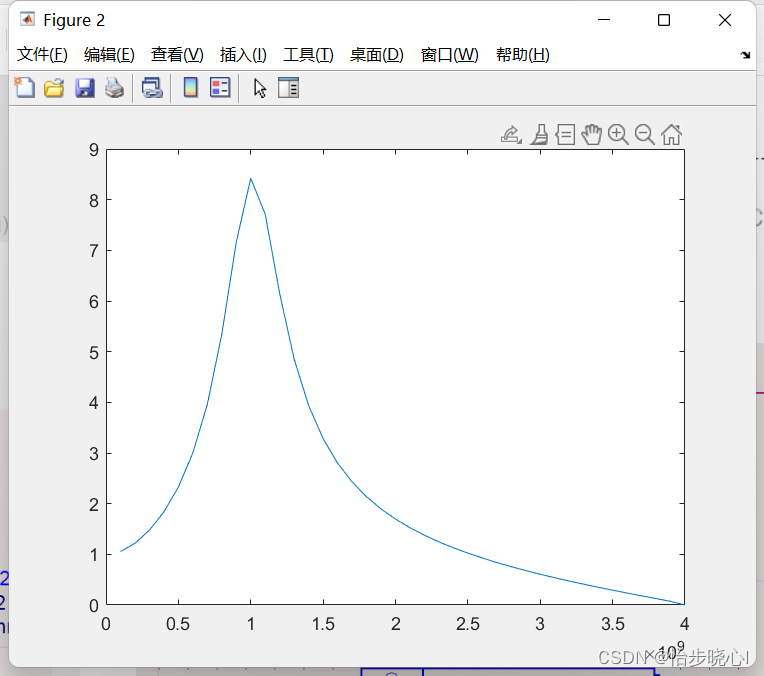
在这里插入图片描述

ADS结构：
在这里插入图片描述

ADS的Zin结果：
在这里插入图片描述

这篇关于基于Matlab的策动点阻抗快速综合库函数-微带线综合的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/358180。

相关文章

综合安防管理平台LntonAIServer视频监控汇聚抖动检测算法优势

综合安防管理平台LntonAIServer视频监控汇聚抖动检测算法优势

LntonAIServer视频质量诊断功能中的抖动检测是一个专门针对视频稳定性进行分析的功能。抖动通常是指视频帧之间的不必要运动，这种运动可能是由于摄像机的移动、传输中的错误或编解码问题导致的。抖动检测对于确保视频内容的平滑性和观看体验至关重要。 优势 1. 提高图像质量 - 清晰度提升：减少抖动，提高图像的清晰度和细节表现力，使得监控画面更加真实可信。 - 细节增强：在低光条件下，抖
阅读更多...
电脑桌面文件删除了怎么找回来？别急，快速恢复攻略在此

电脑桌面文件删除了怎么找回来？别急，快速恢复攻略在此

在日常使用电脑的过程中，我们经常会遇到这样的情况：一不小心，桌面上的某个重要文件被删除了。这时，大多数人可能会感到惊慌失措，不知所措。 其实，不必过于担心，因为有很多方法可以帮助我们找回被删除的桌面文件。下面，就让我们一起来了解一下这些恢复桌面文件的方法吧。 一、使用撤销操作 如果我们刚刚删除了桌面上的文件，并且还没有进行其他操作，那么可以尝试使用撤销操作来恢复文件。在键盘上同时按下“C
阅读更多...
hdu 4565 推倒公式+矩阵快速幂

hdu 4565 推倒公式+矩阵快速幂

题意 求下式的值： Sn=⌈ (a+b√)n⌉%m S_n = \lceil\ (a + \sqrt{b}) ^ n \rceil\% m 其中： 0<a,m<215 0< a, m < 2^{15} 0<b,n<231 0 < b, n < 2^{31} (a−1)2<b<a2 (a-1)^2< b < a^2 解析 令： An=(a+b√)n A_n = (a +
阅读更多...
v0.dev快速开发

v0.dev快速开发

探索v0.dev：次世代开发者之利器 今之技艺日新月异，开发者之工具亦随之进步不辍。v0.dev者，新兴之开发者利器也，迅速引起众多开发者之瞩目。本文将引汝探究v0.dev之基本功能与优势，助汝速速上手，提升开发之效率。 何谓v0.dev？ v0.dev者，现代化之开发者工具也，旨在简化并加速软件开发之过程。其集多种功能于一体，助开发者高效编写、测试及部署代码。无论汝为前端开发者、后端开发者
阅读更多...
matlab读取NC文件（含group）

matlab读取NC文件（含group）

matlab读取NC文件（含group）： NC文件数据结构： 代码： % 打开 NetCDF 文件filename = 'your_file.nc'; % 替换为你的文件名% 使用 netcdf.open 函数打开文件ncid = netcdf.open(filename, 'NC_NOWRITE');% 查看文件中的组% 假设我们想读取名为 "group1" 的组groupName
阅读更多...
利用matlab bar函数绘制较为复杂的柱状图，并在图中进行适当标注

利用matlab bar函数绘制较为复杂的柱状图，并在图中进行适当标注

示例代码和结果如下：小疑问：如何自动选择合适的坐标位置对柱状图的数值大小进行标注？😂 clear; close all;x = 1:3;aa=[28.6321521955954 26.2453660695847 21.69102348512086.93747104431360 6.25442246899816 3.342835958564245.51365061796319 4.87
阅读更多...
利用Django框架快速构建Web应用：从零到上线

利用Django框架快速构建Web应用：从零到上线

随着互联网的发展，Web应用的需求日益增长，而Django作为一个高级的Python Web框架，以其强大的功能和灵活的架构，成为了众多开发者的选择。本文将指导你如何从零开始使用Django框架构建一个简单的Web应用，并将其部署到线上，让世界看到你的作品。 Django简介 Django是由Adrian Holovaty和Simon Willison于2005年开发的一个开源框架，旨在简
阅读更多...
STL经典案例（四）——实验室预约综合管理系统（项目涉及知识点很全面，内容有点多，耐心看完会有收获的！）

STL经典案例（四）——实验室预约综合管理系统（项目涉及知识点很全面，内容有点多，耐心看完会有收获的！）

项目干货满满，内容有点过多，看起来可能会有点卡。系统提示读完超过俩小时，建议分多篇发布，我觉得分篇就不完整了，失去了这个项目的灵魂 一、需求分析 高校实验室预约管理系统包括三种不同身份：管理员、实验室教师、学生 管理员：给学生和实验室教师创建账号并分发 实验室教师：审核学生的预约申请 学生：申请使用实验室 高校实验室包括：超景深实验室（可容纳10人）、大数据实验室（可容纳20人）、物联网实验
阅读更多...
C# double[] 和Matlab数组MWArray[]转换

C# double[] 和Matlab数组MWArray[]转换

C# double[] 转换成MWArray[], 直接赋值就行             MWNumericArray[] ma = new MWNumericArray[4];             double[] dT = new double[] { 0 };             double[] dT1 = new double[] { 0,2 };
阅读更多...
CentOs7上Mysql快速迁移脚本

CentOs7上Mysql快速迁移脚本

因公司业务需要，对原来在/usr/local/mysql/data目录下的数据迁移到/data/local/mysql/mysqlData。 原因是系统盘太小，只有20G，几下就快满了。 参考过几篇文章，基于大神们的思路，我封装成了.sh脚本。 步骤如下： 1） 先修改好/etc/my.cnf,        ##[mysqld]       ##datadir=/data/loc
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2