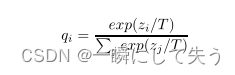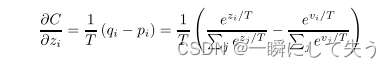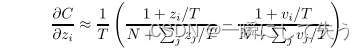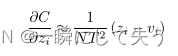本文主要是介绍《Distilling the Knowledge in a Neural Network》知识蒸馏论文解读,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
问题:由于网络结构的复杂,进行预测的代价过高,难以将网络部署到轻量级设备用户中。
解决方法:利用知识蒸馏进行模型压缩,实现轻量级网络。
接下来以这篇论文为基础来认识知识蒸馏。
1、软标签和硬标签
描述:硬标签就是指我们在预测时正确的值为1,错误的值为0。而软标签则认为错误的标签不可能都是零,因为对错误标签而言总有着自己的差距,如下面所示。
硬标签 软标签
宝马 1 0.9
奔驰 0 0.6
垃圾车 0 0.3
胡萝卜 0 0.001
从上面描述可知,在我们预测宝马车时,除了正确的标签归为1,其他的标签都为0,也就是非0即1。但是实际上在错误类别中,宝马更像奔驰而更不像胡萝卜,这说明错误标签的信息也有差距。于是就引入了软标签,将标签值改为0到1之间的值,这样呈现的信息就更为丰富。
2、温度系数T
软标签可以把错误标签的信息呈现出来,但是在呈现时有些错误标签的差距不明显,也就是标签值不够软。这个时候为了把这个不明显的差距变得更为明显,论文作者就引入了温度系数T来改变原来的SoftMax函数,即:
式中qi代表使用SoftMax输出的类别概率、zi代表每个类别的logit、T为温度系数。
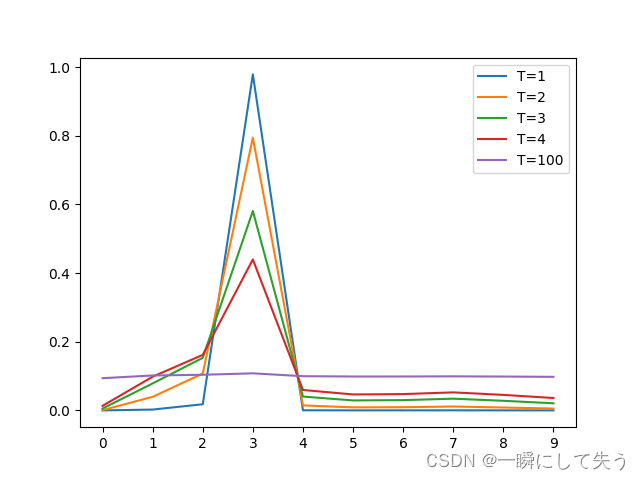
PS:如果T小,错误类别的信息差距较小,但如果T过大,标签就会过软,容易导致平均主义,难以达到预测的效果,具体T的选值效果如下所示。
图中,我们可以看出T越大,曲线越平滑。如果T过大就易出现平均主义,就会变得难以预测。
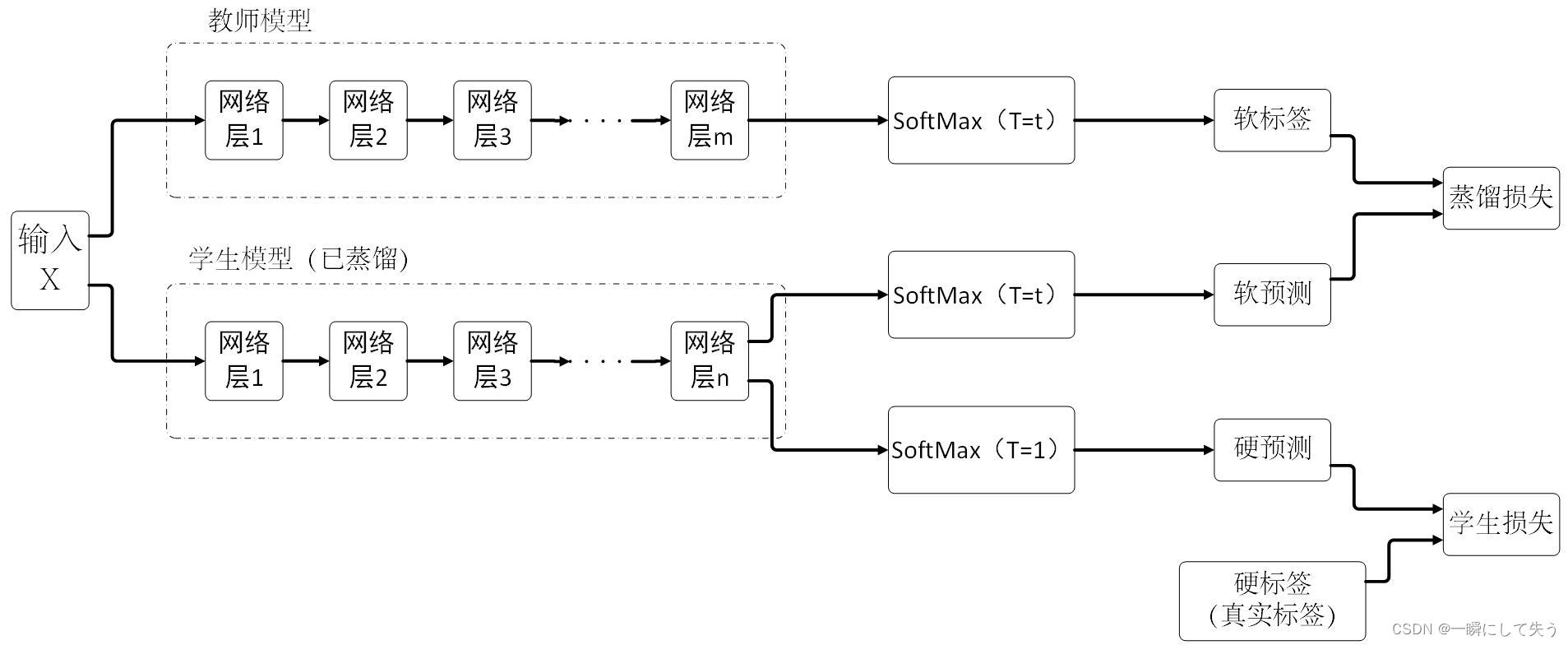
3、知识蒸馏网路框架
图中分别将样本喂入教师模型和学生模型进行训练,其中教师模型为原有的复杂模型,学生模型为压缩后的简单模型。在计算损失时,需要分别计算蒸馏损失和学生损失,蒸馏损失是在温度为T的时候计算教师和学生两个网络输出的交叉熵,而学生损失是在温度为1的情况下计算真实标签和学生网络输出的交叉熵,具体公式如下。
式中共有m个样本和n个类别,y代表真实标签(硬标签) ,P(xij)表示学生网络输出的软标签,Yij表示教师网络输出的软标签,λ表示0到1之间的权重系数。
4、交叉熵梯度
假设教师模型为vi,学生模型为zi,两者分别的软目标概率分布为qi和pi,则梯度为:
1、假设温度系数可以无限大,式子就变形为:
PS:采用
的泰勒展开式, 假如T无限大,则后面几项就可以忽略不计,此时我们取泰勒的前两项,就转变为上面的形式。
2、假设不同样本的logit值为0:
PS:分母里的两个西格玛求和为0。
因此在这两个条件都满足的特例情况下,就转变为求最小化均方误差。
5、结论
为了验证知识蒸馏的效果,论文作者在MINST手写数字集上进行了预实验,然后以语音识别的复杂模型蒸馏来验证了知识蒸馏的性能。
这篇关于《Distilling the Knowledge in a Neural Network》知识蒸馏论文解读的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!