考虑设备动作损耗的配电网分布式电压无功优化（Matlab代码实现）

💥💥💥💞💞💞欢迎来到本博客❤️❤️❤️💥💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

目录

💥1 部分复现

📚2 概述

🎉3 运行结果

👨‍💻4 Matlab代码

💥1 部分复现

📚2 概述

     摘要:电压无功控制是保证配电网经济安全运行的重要任务，协调多种调节手段能提高配电网的运行效率。考虑了有载调压变压器、电压调节器、分组投切电容器和分布式电源逆变器等电压无功调控设备，并针对现有电压无功控制模型存在的无谓动作和求解效率低等问题，提出了一种考虑设备动作损耗的配电网分布式电压无功优化策略。首先，基于支路潮流方程建立了配电网电压无功控制模型，并松弛为混合整数二阶锥规划。同时考虑到设备的动作损耗，提出了基于模型预测控制的滚动优化模式。进一步基于交替方向乘子法实现配电网多区域分布式协同优化。最后，基于改进的 IEEE33节点测试系统进行了仿真。仿真结果表明:所提控制策略能够避免设备的无谓动作，并解决了“维数灾”问题，提高了配电网的电压无功控制效率。

​

🎉3 运行结果

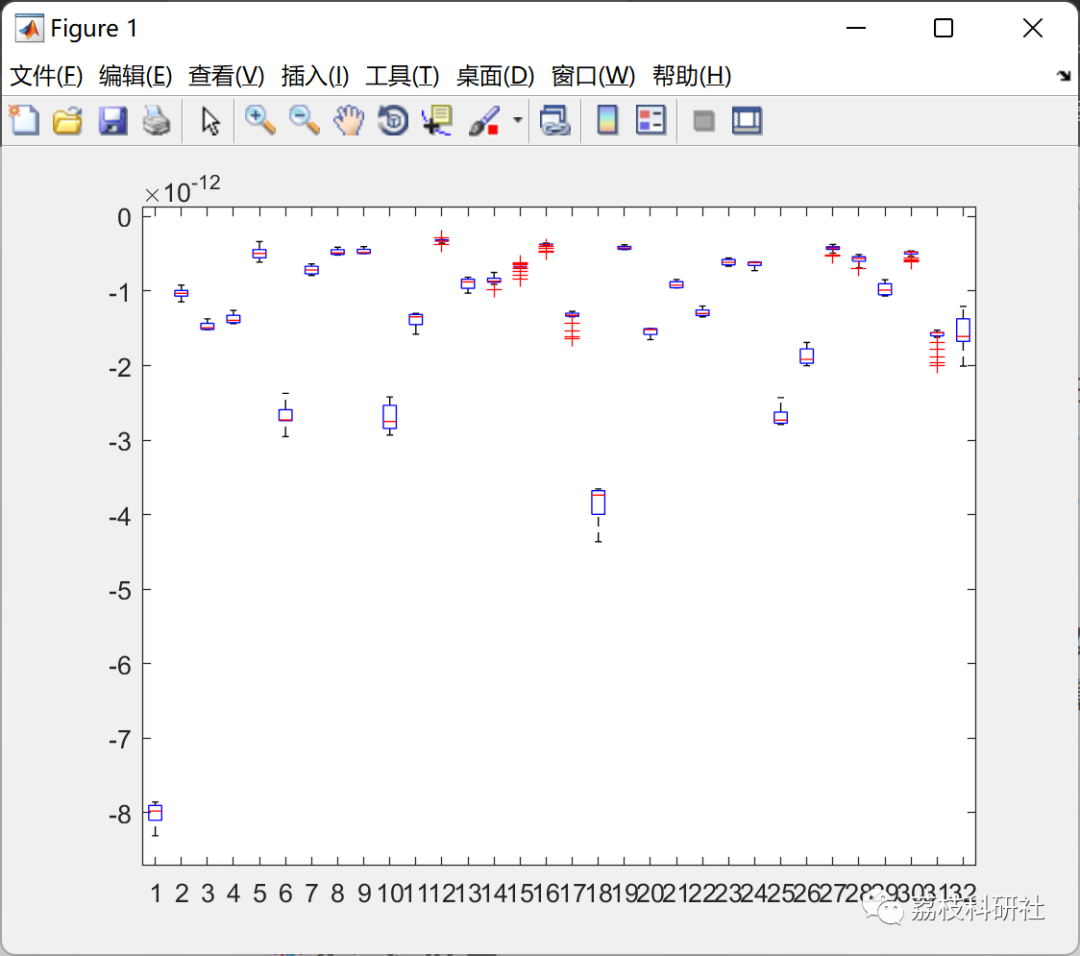
利用IEEE33测试节点算例说明二阶锥松弛的准确性

CPXPARAM_MIP_Display                             1Tried aggregator 1 time.QCP Presolve eliminated 9408 rows and 1704 columns.Aggregator did 336 substitutions.Reduced QCP has 7728 rows, 5712 columns, and 17808 nonzeros.Reduced QCP has 768 quadratic constraints.Presolve time = 0.01 sec. (6.80 ticks)Parallel mode: using up to 16 threads for barrier.Number of nonzeros in lower triangle of A*A' = 34104Using Approximate Minimum Degree orderingTotal time for automatic ordering = 0.00 sec. (2.49 ticks)Summary statistics for Cholesky factor:  Threads                   = 16  Rows in Factor            = 7728  Integer space required    = 12264  Total non-zeros in factor = 83880  Total FP ops to factor    = 1017720 Itn      Primal Obj        Dual Obj  Prim Inf Upper Inf  Dual Inf Inf Ratio   0   3.0337406e+02  -7.6106781e-01  7.30e+03  0.00e+00  6.21e+03  1.00e+00   1   3.0427107e+01   1.6560187e+00  7.30e+03  0.00e+00  6.21e+03  5.54e-01   2   5.5432810e+00   2.6608161e-01  7.32e+02  0.00e+00  6.22e+02  2.69e+00   3   8.5159524e-01  -9.6574600e-02  1.35e+02  0.00e+00  1.15e+02  1.50e+01   4   1.4611180e-01  -6.8774608e-02  2.43e+01  0.00e+00  2.06e+01  6.92e+01   5   5.7055442e-02  -8.7266983e-04  5.49e+00  0.00e+00  4.67e+00  3.22e+02   6   2.8129625e-02   1.9071094e-02  1.46e+00  0.00e+00  1.24e+00  2.37e+03   7   2.5320794e-02   2.3848906e-02  2.27e-01  0.00e+00  1.93e-01  1.82e+04   8   2.5013002e-02   2.4772517e-02  3.65e-02  0.00e+00  3.11e-02  1.42e+05   9   2.4971013e-02   2.4933730e-02  5.92e-03  0.00e+00  5.03e-03  1.32e+06  10   2.4964786e-02   2.4958751e-02  9.10e-04  0.00e+00  7.74e-04  1.07e+07  11   2.4963608e-02   2.4963505e-02  1.47e-04  0.00e+00  1.25e-04  1.63e+09  12   2.4963589e-02   2.4963588e-02  2.48e-06  0.00e+00  2.11e-06  3.29e+11时间已过 3.339317 秒。​Ploss_total =​    2.4964​部分代码：

%定义变量
U=sdpvar(33,24);%电压的平方
I=sdpvar(32,24);%电流的平方
P=sdpvar(32,24);%线路有功
Q=sdpvar(32,24);%线路无功
Pg=sdpvar(33,24);%发电机有功
Qg=sdpvar(33,24);%发电机无功
Pin=-father*P+father*(I.*(r*ones(1,24)))+son*P;%节点注入有功
Qin=-father*Q+father*(I.*(x*ones(1,24)))+son*Q;%节点注入无功
Ploss_total=sum(sum(I.*(r*ones(1,24))));%目标函数，网损最小
%约束条件
C1=[U>=Umin,U<=Umax,Pg>=-Pgmax,Pg<=Pgmax,Qg>=-Qgmax,Qg<=Qgmax];%电压边界
C1=[C1,I>=0,I<=0.11,P>=-0.11,P<=0.11,Q>=-0.11,Q<=0.11];%电流和功率边界
C2=[Pin+Pload-Pg==0];%有功KCL约束
C3=[Qin+Qload-Qg==0];%无功KCL约束
C4=[U(Line(:,2),:)==U(Line(:,1),:)-2*(r*ones(1,24)).*P-2*(x*ones(1,24)).*Q+((r.^2+x.^2)*ones(1,24)).*I];%电压降落约束
C5=[U(Line(:,1),:).*I>=P.^2+Q.^2];%二阶锥约束
C=[C1,C2,C3,C4,C5];
toc%建模时间
ops=sdpsettings('solver','cplex');
result=solvesdp(C,Ploss_total,ops);
toc%求解时间
Ploss_total=100*double(Ploss_total)
P=double(P);Q=double(Q);U=double(U);I=double(I);
error=P.^2+Q.^2-U(Line(:,1),:).*I;
boxplot(error')

👨‍💻4 Matlab代码