本文主要是介绍25.3 matlab里面的10中优化方法介绍——Nelder-Mead法(matlab程序),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1.简述
fminsearch函数用来求解多维无约束的线性优化问题
用derivative-free的方法找到多变量无约束函数的最小值
语法
x = fminsearch(fun,x0)
x = fminsearch(fun,x0,options)
[x,fval] = fminsearch(...)
[x,fval,exitflag] = fminsearch(...)
[x,fval,exitflag,output] = fminsearch(...)
解释
fminsearch能够从一个初始值开始,找到一个标量函数的最小值。通常被称为无约束非线性优化
x = fminsearch(fun,x0) 从x0开始,找到函数fun中的局部最小值x,x0可以是标量,向量,矩阵。fun是一个函数句柄
x = fminsearch(fun,x0,options) 以优化参数指定的结构最小化函数,可以用optimset函数定义这些参数。(见matlab help)
[x,fval] = fminsearch(...)返回在结果x出的目标函数的函数值
[x,fval,exitflag] = fminsearch(...) 返回exitflag值来表示fminsearch退出的条件:
1--函数找到结果x
0--函数最大功能评价次数达到,或者是迭代次数达到
-1--算法由外部函数结束
[x,fval,exitflag,output] = fminsearch(...) 返回一个结构输出output,包含最优化函数的信息:output.algorithm 使用的优化算法
output.funcCount 函式计算次数
output.iterations 迭代次数
output.message 退出信息
另外
fun是需要最小化的函数,他的输入为input,输出为标量f,目标函数在x上作出估计,函数可以为M文件的一个句柄函数(当是M文件时,用单引号括起文件名):
functionx = fminsearch(@myfun, x0)
这里function f = myfun(x)
f = ... 其自变量为x
或者直接写出
asx = fminsearch(@(x)sin(x^2), x0);
算法
fminsearch使用单纯型法,这是一种不会使用数值或者梯度分析的直接的方法
假如x的长度为n,那么会有n+1个顶点,两维空间中,单纯型是三角形,三维空间,他是一个锥形。搜索的每一步中,都会产生离当前单纯型比较近的点,在新的点上的函数值回合单纯型各个顶点上的值比较,一般都会有一个定点被替代,产生一个新的单纯型,重复步骤,直到单纯型的大小小于阈值。
限制
fminsearch可以处理不连续的问题,如果得不到全局最优,则其会得到局部最优
它只能最小化时数,复数并不在其能力范围之内,且f(x)的返回值也必须是时数,如果x为复数,则其必须分解为实部和虚部两部分。
我们可以稍微对进行一些变换,就可实现利用fminsearch进行参数估计。
2.代码
主程序:
%% 用Nelder-Mead方法求最优化解
f1203 = inline('x(1)*(x(1)-5-x(2))+x(2)*(x(2)-4)','x');
x0 = [0 4];
TolX = 1e-4;
TolFun = 1e-9;
MaxIter = 100;
[xN,fN] = Opt_Nelder(f1203,x0,TolX,TolFun,MaxIter)
%取最小值点以及此处的最小值
[xF,fF] = fminsearch(f1203,x0) %用MATLAB内置函数fminsearch求解
子程序;
function [xo,fo] =Opt_Nelder(f,x0,TolX,TolFun,MaxIter)
%Nelder-Mead法用于多维变量的最优化问题,维数>=2.
N = length(x0);
if N == 1 %一维情况,用二次逼近计算
[xo,fo] = Opt_Quadratic(f,x0,TolX,TolFun,MaxIter);
return
end
S = eye(N);
for i = 1:N %自变量维数大于2时,重复计算每个子平面的情况
i1 = i + 1;
if i1 > N
i1 = 1;
end
abc = [x0; x0 + S(i,:); x0 + S(i1,:)]; %每一个定向子平面
fabc = [feval(f,abc(1,:)); feval(f,abc(2,:)); feval(f,abc(3,:))];
[x0,fo] = Nelder0(f,abc,fabc,TolX,TolFun,MaxIter);
if N < 3 %二维情况不需重复
break;
end
end
xo = x0;
3.运行结果

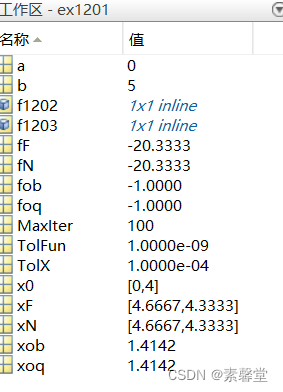
这篇关于25.3 matlab里面的10中优化方法介绍——Nelder-Mead法(matlab程序)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




