curve25519-c++调用，...转换成椭圆曲线上的一个点。

目录

一.问题说明：

二.如何解决这个问题：

1.尝试使用openssl-EC库——失败：

2.使用EVP获得25519曲线，从而实现打点。——失败；

3.curve25519——成功。

三.总结：

一.问题说明：

1.为什么需要将数据转换成椭圆曲线上的一个点？

很多的情况下有些人会用x*G*a来进行椭圆曲线的加密，或者签名,x为数据，G为基点，a为随机盲化值，发送给其他方，另一方再计算x*G*a*b，发送给发送方，发送方计算x*G*a*b*a^(-1)，若接收方也拥有x，可以计算x*G*b，相同，就完成了求交。但是只能用一次，因为发送方知道x，所以可以算出x*G*b*x^(-1)，若想对其他x加密或者签名都是比较简单的，若想持续使用必须保证每次b是不同的，其实可以想一下，b如果不同，假如接收方x1对应b1，但发送方并不知道b1对应哪个x，所以他要将所有数据都算一下，复杂度可达n^2,传输开销也是问题。

其实可以看出其中最大的问题是可以消掉x，获得b*G，如何解决问题，就是打点，将数据x转化成椭圆曲线上的一个点H(x)，计算a*H(x)，从而解决这个问题，当然这个方案不抗恶意参与方，若发送方仍旧使用上面的方案恶意获得也是可以破解的。对于这个问题可以进行一定程度的验证。（发送方将所有点乘以x^(-1)，若存在多个相同的点，那么说明这个接收方是恶意的）。

二.如何解决这个问题：

请记住上面最重要的问题是打点，对于点乘，求逆都是次要的。

1.尝试使用openssl-EC库——失败：

大概像这样，去建立一个曲线获得一对公钥私钥。

bool get_keypair(EC_KEY** key, bool getcompressed,uint8_t* rawprikey,  uint8_t rawprikeylen) {BIGNUM* priv; //prikey bignumBN_CTX* ctx; //hold the operationconst EC_GROUP* group;EC_POINT* pub; //pubkey point st*key = EC_KEY_new_by_curve_name(NID_secp256k1); //secp256k1, !!!crashed hereif (*key == 0) {printf("new ec key failed");exit(-1);}priv = BN_new(); //create bignumBN_bin2bn(rawprikey, 32, priv); //fill the bigbum with prikeyEC_KEY_set_private_key(*key, priv); //put prikey bignum to key pairctx = BN_CTX_new(); //create contextBN_CTX_start(ctx); //init contextgroup = EC_KEY_get0_group(*key); //Gpub = EC_POINT_new(group); //create pub stEC_POINT_mul(group, pub, priv, NULL, NULL, ctx); //P = n * GEC_KEY_set_public_key(*key, pub); //fill the key pair, !!!crashed hereEC_KEY_set_conv_form(*key, getcompressed ? POINT_CONVERSION_COMPRESSED : POINT_CONVERSION_UNCOMPRESSED); //compressd or not uint64_t pubkeylen = i2o_ECPublicKey(*key, NULL);uint8_t *pubkey = calloc(pubkeylen, sizeof(uint8_t));uint8_t* pub_copy = pubkey;if (i2o_ECPublicKey(*key, &pub_copy) != pubkeylen) {puts("Unable to decode public key");return false;}/*for (int i = 0; i < *pubkeylen; i++) {printf("%02X", (*pubkey)[i]);}*/EC_POINT_free(pub);//free allBN_CTX_end(ctx);BN_CTX_free(ctx);BN_clear_free(priv);return true;
}

我尝试去打点，那么我我需要计算一个数据对应的x和y坐标。然后我去了解一下怎么计算这个过程。找了一些相关代码hash2point，和相关论文，他们是这个思路：

 一个数转换hash成256，然后带人这个曲线对应的方程，然后尝试开根是不是一个整数，若是则获得x,y，如果不是则x+1，继续。方案理论可行，但是开根的函数计算开销很大。为了计算一个点就要耗费巨大算力，对于大量的数据这个算力将难以支持。所以我选择堵死这条路。

2.使用EVP获得25519曲线，从而实现打点。——失败；

首先说明一下为什么突然转折，走向了X25519这条曲线：因为它有一个十分关键的性质，任何一个x都可以转化成一个点，不需要确定坐标y，这将省去上面算力过大的问题。而且后面验证这个思路是完全正确的。至于详细的介绍可参考X25519（Curve25519）椭圆曲线参考资料 - 简书关键性质这里有提到：深入理解X25519 - 知乎

那么如何引入X25519，很多博客说OPENSSL1.1.1之后都支持了该曲线，我想说不会就别误人子弟，那些只会翻译的弟弟，问什么这么生气，因为不知一篇博客说了可以，我用了大量的精力去尝试这个方案，但是答案是这完全不可行，比如：OpenSSL在使用X25519时的小坑_qmickecs的博客-CSDN博客_x25519

EVP_PKEY_CTX *pctx, *kctx;
EVP_PKEY *pkey = NULL, *params = NULL;/* Create the context for parameter generation */
if(NULL == (pctx = EVP_PKEY_CTX_new_id(EVP_PKEY_EC, NULL))) handleErrors();/* Initialise the parameter generation */
if(1 != EVP_PKEY_paramgen_init(pctx)) handleErrors();/* We're going to use the ANSI X9.62 Prime 256v1 curve */
if(1 != EVP_PKEY_CTX_set_ec_paramgen_curve_nid(pctx, NID_X9_62_prime256v1)) handleErrors();/* Create the parameter object params */
if (!EVP_PKEY_paramgen(pctx, &params)) handleErrors();/* Create the context for the key generation */
if(NULL == (kctx = EVP_PKEY_CTX_new(params, NULL))) handleErrors();/* Generate the key */
if(1 != EVP_PKEY_keygen_init(kctx)) handleErrors();
if (1 != EVP_PKEY_keygen(kctx, &pkey)) handleErrors();

说这是调用常用曲线的方案，若用X25519用下面思路：

EVP_PKEY_CTX *pctx;
EVP_PKEY *pkey= NULL;/* Create the context for parameter generation */
if (NULL == (pctx = EVP_PKEY_CTX_new_id(NID_X25519, NULL))) handleErrors();/* Generate the key */
if (1 != EVP_PKEY_keygen_init(pctx)) handleErrors();
if (1 != EVP_PKEY_keygen(pctx, &pkey) handleErrors();

好的没问题，你没发现pkey=NULL吗，EVP是一个封装好的库，里面没有点乘，所以必须将EVP的曲线转到EC上使用，要用这个EVP_PKEY_get0_EC_KEY，pkey是空的。。。对于如何使用EVP转化成EC，再使用EC点乘有个案例：

SM2实现（利用openssl的evp） - 20181204王浩博 - 博客园后来阅读OPENSSL开发者说法明白，人家说不会支持X25519这个曲线，因为这个曲线很特殊，他们不会封装这个曲线在曲线库里面，因为这个曲线“不一样”！

3.curve25519——成功。

使用这个方案也是历经磨难，感谢同事之源！curve25519库的链接

任何一个数转化成char[32]，它内部就可以自行转化成一个点。

库引入时候注意加入：

extern "C" {
#include "thirdparty/curve25519/curve25519-donna-c64.h"
}

简单封装了两个函数：

unsigned char* curve25519_point_div_value(char * order_dec, unsigned char base_point[32]){//const char * curve_order_8q = "57896044618658097711785492504343953926856930875039260848015607506283634007912";//const char * curve_order_4r = "57896044618658097711785492504343953926413053790601303191441976501629495631988";unsigned char G_mut_order_point[32];mpz_t integer_a;mpz_init2(integer_a,256);mpz_set_str(integer_a, order_dec, 10);mpz_t inv_a;mpz_t mod_num;mpz_init(inv_a);mpz_init(mod_num);int flag = 0;if(!curve25519_donna(G_mut_order_point, curve_order_8q, base_point) && check(G_mut_order_point, base_point)) {mpz_set_str(mod_num, "57896044618658097711785492504343953926856930875039260848015607506283634007912", 10);flag = 8;}if(!curve25519_donna(G_mut_order_point, curve_order_4r, base_point) && check(G_mut_order_point, base_point)){mpz_set_str(mod_num, "57896044618658097711785492504343953926413053790601303191441976501629495631988", 10);flag = 4;}unsigned char inv_a_char[32];mpz_invert(inv_a, integer_a, mod_num);for(auto i=0;i<4;i++){memcpy(inv_a_char+i*8,&inv_a->_mp_d[i],8);}static unsigned char final_res[32];curve25519_donna(final_res, inv_a_char, base_point);return final_res;
};unsigned char* curve25519_point_mut_value(char * order_dec, unsigned char base_point[32]){mpz_t integer_a;mpz_init2(integer_a,256);mpz_set_str(integer_a, order_dec, 10);auto* a_char = new unsigned char[32];for(auto i=0;i<4;i++){memcpy(a_char+i*8,&integer_a->_mp_d[i],8);}static unsigned char res[32];curve25519_donna(res, a_char, base_point);return res;
}

这里的模数的阶是写死的，为什么呢，这里处以一个数我们需要计算一个数的模逆，其实有些方案说2，4，8，q，2q，4q，8q，r，2r，4r这几种可能，在论文里有写判定条件，但是我判定条件好麻烦，索性直接强行判断，该数乘模数+1回到该点，而且这个库的开发文章说就8q，和4q两种可能，所以计算除法的思路是先求模数，即乘以这两个数回到该点的数；再求逆，我使用的方案是该数转大数，大数求逆，再转回来：X25519说明

​​​​​​​

用python算一下： 

q = 2**252 + 27742317777372353535851937790883648493
r = 2**253 - 55484635554744707071703875581767296995print(r * 4)
print(q * 8)
q_2 = r * 4
q_3 = ""
for i in range(32):q_1 = q_2 % 256q_2 = int(q_2 // 256)q_3+= str(q_1)+","

unsigned char curve_order_8q[32] = {105,159,174,231,210,24,147,192,178,230,188,23,245,206,247,166,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,128};
unsigned char curve_order_4r[32] = {117,96,81,24,45,231,108,63,77,25,67,232,10,49,8,89,255,255,255,255,255,255,255,255,255,255,255,255,255,255,255,127};

但还没完，我尝试使用这个库去签名是没问题的，但是不能实现除，你会发现a*H(x)*a^(-1)!=H(x)，怎么回事呐，是库有问题。。。找啊找，终于知道了；

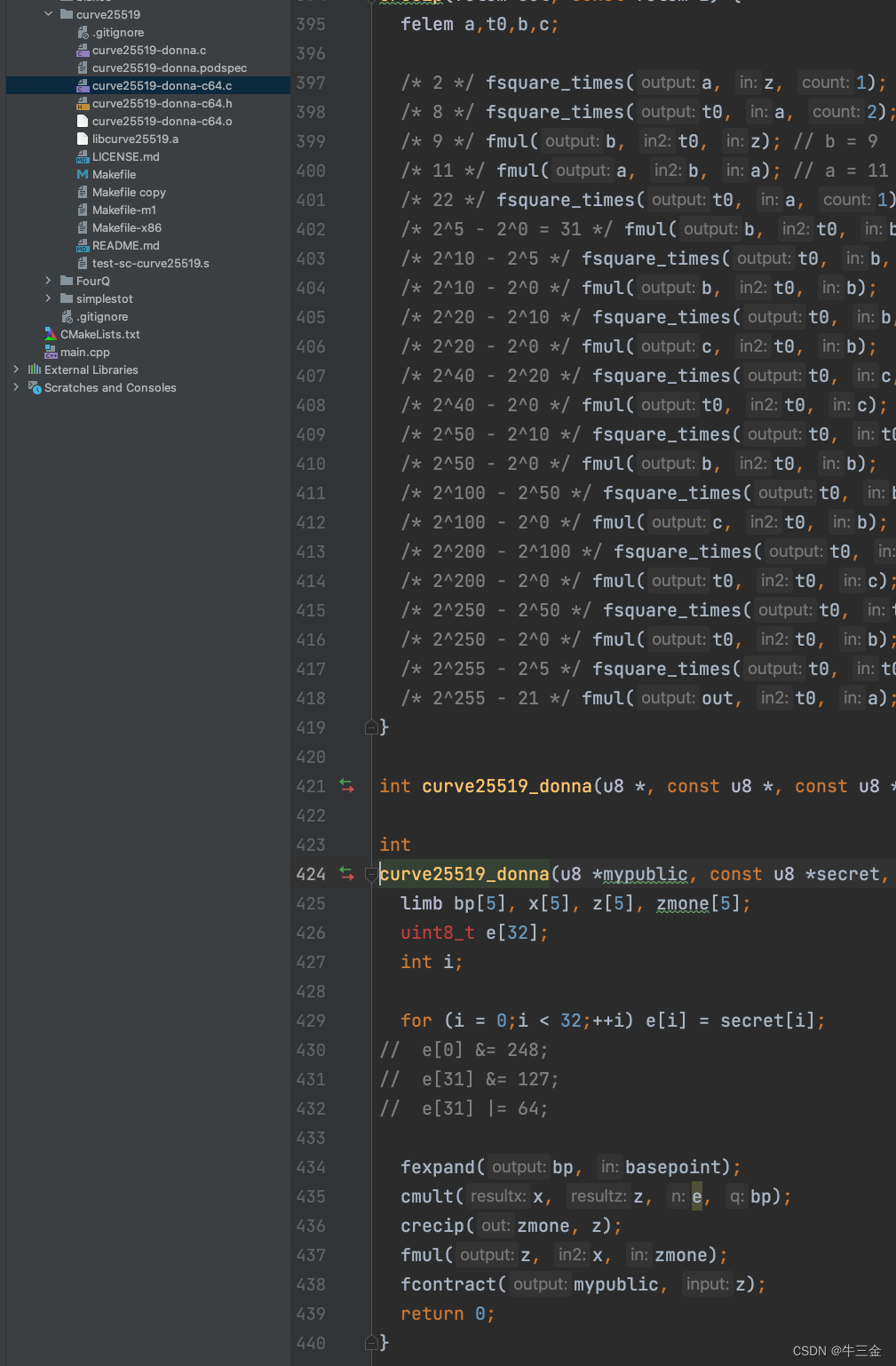
 这里需要将这几行注释掉，他们说这样做了优化，签名会快一些，但会导致一些问题。需要可到我空间自行下载。ECC-X25519，打点，点乘，点除-网络安全文档类资源-CSDN下载

三.总结：

这个开发过程维持1周多，尝试了很多思路，这三个是主要尝试的方案，当然还有其他思路比如尝试使用双层加密打点，但是还是存在安全问题。也算苦尽甘来，在这周中进度很慢很慢，甚至怀疑下周是不是能完成，下个库会不会又大失所望，比如啊，在使用EC库的时候，乘法除法都写好了，甚至整个代码都完成了但是最终还是打点失败，EVP说又25519，可压根转不过去。卡在一个没有把握解决的问题上真的会十分忧虑，但还好有同事的支援，有坚持，该庆祝一下，睡个安稳觉！！！