cv姿态评估：Levenberg-Marquardt优化-阻尼最小二乘（DLS）

本文主要是介绍cv姿态评估：Levenberg-Marquardt优化-阻尼最小二乘（DLS），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

'''
自己整理备忘，也供后人参考。
KZ@njucs.onMicrosoft.com本节记录了cv姿态评估的常见思路，建立模型的方法与Levenberg-Marquardt优化原理。
在下一节中，我们将讨论如何在工程上将旋转向量、欧拉角与四元数之间进行转换。
'''

基础知识：

仿射变换是计算机视觉领域应用十分广泛的特殊变换。是指在几何中，一个向量进行一次线性变换并接上一个平移，变换为另一个向量。对于一个三维直角坐标系，基于每个坐标轴的旋转具有的规则旋转空间的集合，可以表示任何三维向量。在有限维的情况，每个仿射变换可以由一个矩阵A和一个向量b给出，对应于一个矩阵和一个向量的乘法，而仿射变换的复合对应于普通的矩阵乘法，只要加入一个额外的行到矩阵的底下，这一行全部是0除了最右边是一个1，而列向量的底下要加上一个1。

一个对向量平移向量b，与旋转放大缩小 A的仿射映射为

在齐次坐标上，等价于

在分形的研究里，收缩平移仿射映射可以制造制具有自相似性的分形。一个在两个仿射空间之间的仿射变换，是在向量上呈现线性之坐标点的变换（即为空间中点与点之间的向量）。以符号表示的话，使得，决定任一对点的线性变换：

或者

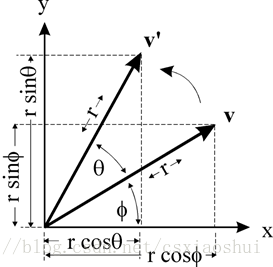
在二维坐标系上绕原点进行的二维旋转：

如图所示，当点v绕原点转动θ至v'，假设v点的坐标是(x,y)，那么可以推导得到v'(x',y')，过程如下：

参数如图，我们发现：

x=rcosϕ

y=rsinϕ

x′=rcos(θ+ϕ)

y′=rsin(θ+ϕ)

通过三角函数展开得：

x′=rcosθcosϕ−rsinθsinϕ

y′=rsinθcosϕ+rcosθsinϕ

代入x,y表达式可得：

x′=xcosθ−ysinθ

y′=xsinθ+ycosθ

使用矩阵表示：

绕任意轴的三维旋转

绕任意轴的三维旋转可以将旋转分解为一系列基本的二维旋转，如图所示：

步骤一，二，三

什么是姿势估计？

在计算机视觉中，物体的姿势指的是其相对于相机的相对取向和位置。通过相对于相机移动对象或相对于对象移动相机来更改姿势。

姿势由上下翻转（pitch），左右翻转（yaw），平面内旋转（roll）构成。

比如，人脸姿态估计的思想：旋转三维标准模型一定角度，直到模型上“三维特征点”的“2维投影”，与待测试图像上的特征点（图像上的特征点显然是2维）尽量重合。这时候我们脑海中就应该浮现出一种诡异的场景：在幽暗的灯光中，一个发着淡蓝色光芒的人皮面具一点点的“自我调整”，突然一下子“完美无缺”的“扣在了你的脸上”。这就是人脸姿态估计的思想。

计算图像中对象的3D姿势，需要以下几个参量：

1.几个点的2D坐标。

在工程中，通常使用dlib的detector。

2.相同点的3D位置

代表2D要素点的3D位置。理想情况下需要照片中人物的3D模型才能获得3D位置。但在实践中，通用3D模型就足够了。只需要在某个任意参考系中的几个点的3D位置。通常来说，使用以下3D点。

鼻尖：（0.0,0.0,0.0）
下巴：（0.0，-330.0，-65.0）
左眼左角：（ - 225.0f，170.0f，-135.0）
右眼右角：（225.0,170.0，-135.0）
口的左角：（ - 150.0，-150.0，-125.0）
嘴角：（150.0，-150.0，-125.0）

3.相机的光学参数

相机的光学参数包括图像的光学中心和径向失真参数，所以我们必须校准相机。具体方法在这里不再多说，我们假设相机已经被校准。

姿态估计算法原理

这里有三个坐标系。上面显示的各种面部特征的3D坐标是世界坐标。如果我们知道旋转和平移参量，我们可以将世界坐标中的3D点转换为相机坐标中的 3D点。可以使用相机的固有参数（焦距，光学中心等）将相机坐标中的3D点投影到图像平面（即图像坐标系）上。

假设我们知道世界坐标中 $（U，V，W）$ 3D点的位置 $P$ 。如果我们知道相对于相机坐标的世界坐标的旋转 $\ mathbf {R}$ （3×3矩阵）和平移 $\ mathbf {吨}$ （3×1矢量），我们可以使用以下等式计算相机坐标系 $（X，Y，Z）$ 中点的位置 $P$ 。

将它展开：

如果我们知道足够数量的点对应（即 $（X，Y，Z）$ 和 $（U，V，W）$ ），上面就是一个线性方程组，其中 $R_ {} IJ$ 和 $（t_x，t_y，t_z）$ 是未知数，可以很容易被求出。

3D模型上的许多点（即 $（U，V，W）$ ）是给出的，但我们不知道 $（X，Y，Z）$ 。我们只知道2D点的位置（即 $（x，y）$ ）。在不考虑径向畸变的情况下，图像坐标中 $（x，y）$ 的点 $p$ 的坐标由下式给出

$\ begin {align *} \ begin {bmatrix} x \\ y \\ 1 \ end {bmatrix}＆= s \ begin {bmatrix} f_x＆0＆c_x \\ 0＆f_y＆c_y \\ 0＆0＆1 \ end {bmatrix} \ begin {bmatrix} X \\ Y \\ Z \ end {bmatrix} \ end {align *}$

其中， $F_X$ 和 $f_y$ 是在x和y方向上的焦距，并且 $（c_x，c_y）$ 是光学中心。

$小号$ 是一个未知的比例因子，因为在任何图像中我们都不知道深度。我们将矩阵[X,Y,Z]代入以上矩阵。

$\ begin {align *} s \ begin {bmatrix} X \\ Y \\ Z \ end {bmatrix} = \ begin {bmatrix} r_ {00}ï¼r_ {01}ï¼r_ {02}ï¼t_ {x} \ \ r_ {10}ï¼r_ {11}ï¼r_ {12}ï¼t_ {y} \\ r_ {20}ï¼r_ {21}ï¼r_ {22}ï¼t_ {z} \\ \ end {bmatrix} \ begin {bmatrix} U \\ V \\ W \\ 1 \ end {bmatrix} \ end {align *}$

是不是看起来有点复杂？这里使用一种称为直接线性变换(DLT)的方法，可以解决上述形式的等式。

但DLT方法不是非常准确。首先，旋转 $\ mathbf {R}$ 具有三个自由度，但DLT解决方案中使用的矩阵表示具有9个数字。DLT解决方案中没有任何内容迫使估计的3×3矩阵成为旋转矩阵。更重要的是，DLT解决方案不会最小化正确的目标函数。

Levenberg-Marquardt优化

莱文贝格－马夸特方法（Levenberg–Marquardt algorithm）能提供数非线性最小化（局部最小）的数值解。此算法能借由执行时修改参数达到结合高斯-牛顿算法以及梯度下降法的优点，并对两者之不足作改善（比如高斯-牛顿算法之反矩阵不存在或是初始值离局部极小值太远）。

假设 $f$ 是一个从 $\Re ^{m}\rightarrow \Re ^{n}$ 的非线性映射，也就是说 ${\mathbf {P}}\in \Re ^{m}$ 且 ${\mathbf {X}}\in \Re ^{n}$ , 那么， $f({\mathbf {P}})={\mathbf {X}}$

我们希望任意给定一个 $\mathbf {x}$ 以及合理的初始值 ${\mathbf {p}}_{0}$ ，我们能找到一个 ${\mathbf {p}}^{{+}}$ ，使得 ${\mathbf {\epsilon }}^{T}{\mathbf {\epsilon }}$ 尽量小（局部极小），其中 ${\mathbf {\epsilon }}=f({\mathbf {p}}^{+})-{\mathbf {x}}$ 。

我们通过迭代实现最小化，首先根据泰勒展开式我们能把 $f({\mathbf {p}}+{\mathbf {\delta _{p}}})$ 写为下面的近似，这有两个好处：

第一是线性的、第二是只需要一阶微分。

$f({\mathbf {p}}+{\mathbf {\delta _{p}}})\approx f({\mathbf {p}})+{\mathbf {J\delta _{p}}}$

其中 $\mathbf {J}$ 是 $f$ 的雅克比矩阵。对于每次的迭代我们实际上做了这样一件事：

假设这次 iteration 的点是 ${\mathbf {p}}_{k}$ ，我们要找到一个 ${\mathbf {\delta }}_{{{\mathbf {p}},k}}$ 让 $|{\mathbf {x}}-f({\mathbf {p}}+{\mathbf {\delta }}_{{{\mathbf {p}},k}})|\approx |{\mathbf {x}}-f({\mathbf {p}})-{\mathbf {J{\mathbf {\delta }}_{{{\mathbf {p}},k}}}}|=|{\mathbf {\epsilon }}_{{k}}-{\mathbf {J{\mathbf {\delta }}_{{{\mathbf {p}},k}}}}|$ 最小。根据投影公式我们知道当下面式子被满足的时候能有最小误差：