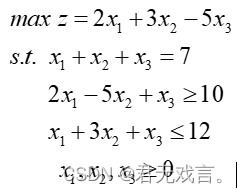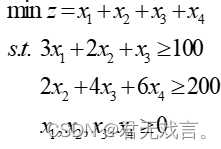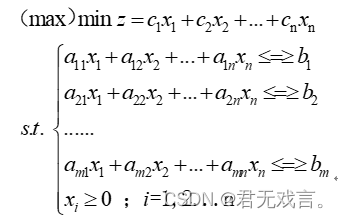最优化方法（基于lingo）之 求解线性规划问题(1/6)

一、实验目的：

1. 会建立合理的规划模型；

2. 学习掌握Matlab中求解线性规划的命令；

[x,fval]=linprog(f,A,b);

[x,fval]=linprog(f,A,b,Aeq,beq);

[x,fval]=linprog(f,A,b,Aeq,beq,lb;ub);

3. 要求学生能在计算机上应用各种优化软件包熟练地操作，解决一些实际应用案例；

4. 预习求解线性规划的单纯形法的基本理论思想。

• 实验内容

1.题目：求解线性规划问题：

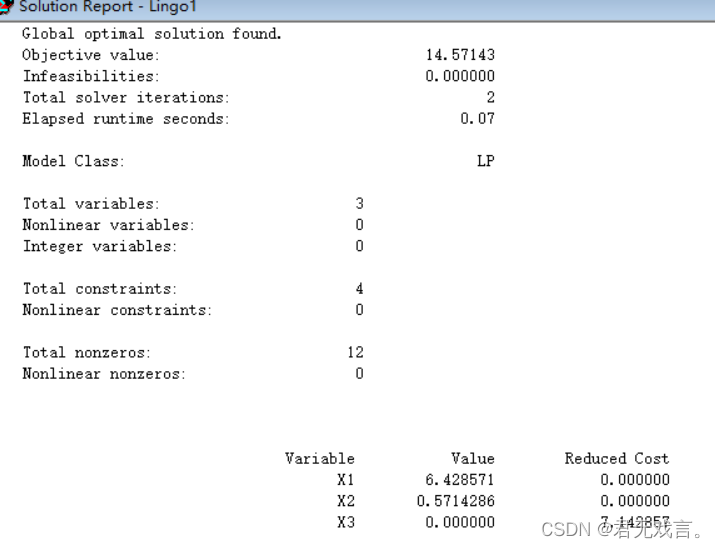
程序代码：

MODEL:
MAX=2*X1+3*X2-5*X3;

X1+X2+X3=7;

2*X1-5*X2+X3>10;

X1+3*X2+X3<12;

END

!LINGO>符号相当于>=

!LINGO<符号相当于<=

!LINGO默认x1，x2>=0

程序执行结果：

结果解释：

当x1等于6.428571，x2等于0.5714286，x3等于0时，z取得最大为14.57143

2.题目：求解线性规划问题：

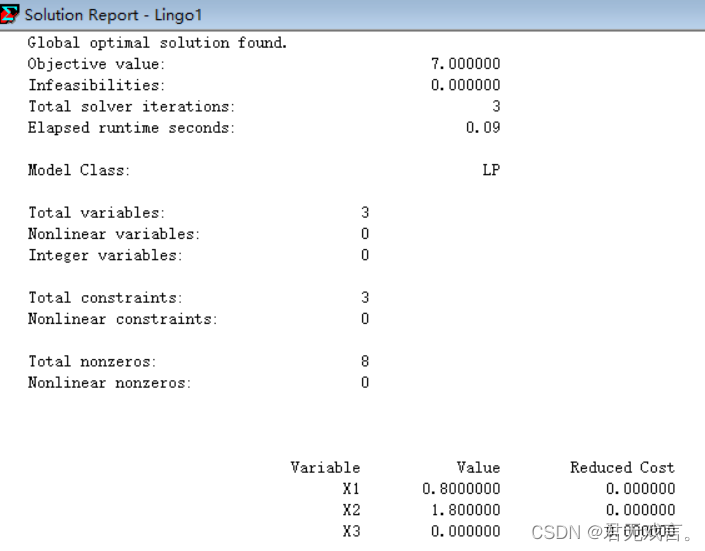
程序代码：

MODEL:
MIN=2*X1+3*X2+X3;

X1+4*X2+2*X3>8;

3*X1+2*X2>6;

END

!LINGO>符号相当于>=

!LINGO<符号相当于<=

!LINGO默认x1，x2,X3>=0

程序执行结果：

结果解释：

当x1等于0.8，x2等于1.8，x3等于0时，z取得最小为7

3.题目：某厂计划在下一个生产周期内生产甲、乙两种产品，需要消耗A1、A2、A3三种资源（例如钢材、煤炭和设备台时），已知每件产品对这三种资源的消耗，这三种资源的现有数量和每件产品可获得的利润如表所示。问如何安排生产计划，使得既能充分利用现有资源，又使总利润最大？

数学模型：设生产甲产品x1件，生产乙产品x2件,可以得到如下数学模型：

程序代码：

MODEL:
MAX=10*X1+18*X2;

5*X1+2*X2<170;

2*X1+3*X2<100;

X1+5*X2<150;

END

!LINGO>符号相当于>=

!LINGO<符号相当于<=

!LINGO默认x1，x2>=0

程序执行结果：

结果解释：

       当生产甲商品8件，乙商品28件时，总利润达到最大为584。

题目：4.求解线性规划问题：假定现有一批某种型号的圆钢长8m，需要截取2.5m的毛坯100根、长1.3m的毛坯200根，问应该怎样选择下料方式，才能既满足需要，又使总的下料最小？

数学模型：一根8M的圆钢截取成2.5m和1.3m的毛坯一共有X1，X2，X3，X4四种方案，具体如下：

由表可以得到如下数学模型：

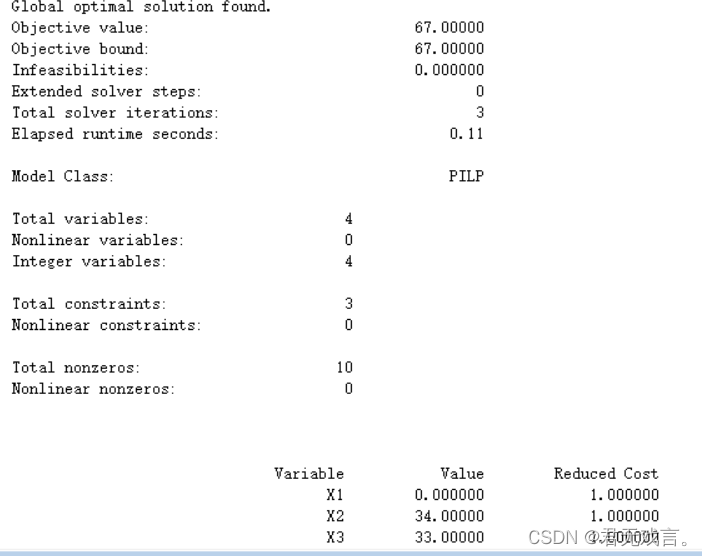
程序代码：

MODEL:
MIN=X1+X2+X3+X4;

3*X1+2*X2+X3>100;

2*X2+4*X3+6*X4>200;

@GIN(X1);

@GIN(X2);

@GIN(X3);

@GIN(X4);

END

!LINGO>符号相当于>=

!LINGO<符号相当于<=

!LINGO默认x1，x2,X3,X4>=0

!@GIN(X1)表示对进行整数约束

程序执行结果：

结果解释：

当执行x2方案34次，x3方案33次时使总下料最少为67。即用34根圆钢切割成68根2.5m的毛坯和1.3m的毛坯，再用33根圆钢切割成33根2.5m的毛坯和132根1.3m的毛坯使总下料最少为67根8m的圆钢。

分析与讨论：

1. 一般线性规划的建模过程？

①分析问题,找出决策变量。

②找出等式或不等式约束条件。

③构造关于决策变量的一个线性函数

1. 线性规划模型的一般形式？