1301:大盗阿福(史上最全题解,没有之一,3种解法各大优化齐上阵)

题目描述】

【输入】

【输出】

【输入样例】

2
3
1 8 2
4
10 7 6 14

【输出样例】

8
24

【提示】

那么代码如下: 

#include <bits/stdc++.h>
using namespace std;
int n,a[100007],dp[100007][2],t;
int main()
{cin>>t;while(t--){memset(a,0,sizeof(a));memset(dp,0,sizeof(dp));cin>>n;for(int i = 1; i <= n; i++) cin>>a[i];dp[1][1] = a[1];dp[1][0] = 0;for(int i = 2; i <= n; i++){dp[i][0] = max(dp[i - 1][0],dp[i - 1][1]);dp[i][1] = a[i] + dp[i - 1][0];}cout<<max(dp[n][0],dp[n][1])<<endl;}return 0;
}

二，优化写法

这道题也可以由一维数组来写。

1. 确定dp数组（dp table）以及下标的含义:dp[i]：考虑下标i（包括i）以内的房屋，最多可以偷窃的金额为dp[i]。
2. 确定递推公式:决定dp[i]的因素就是第i房间偷还是不偷。如果偷第i房间，那么dp[i] = dp[i - 2] + a[i] ，即：第i-1房一定是不考虑的，找出 下标i-2（包括i-2）以内的房屋，最多可以偷窃的金额为dp[i-2] 加上第i房间偷到的钱。如果不偷第i房间,dp[i]=max(dp[i-2],dp[i - 3] + a[i - 1]);,不过在这里因为我们最后是要取最大值的,而dp[i-2]一定是小于等于前面的dp[i-2]+a[i]的，所可以把它省略,最后就变成了dp[i - 3] + a[i - 1]。然后dp[i]取最大值，即dp[i] = max(dp[i - 2] + a[i], dp[i - 3] + a[i - 1]);
3. dp数组如何初始化:根据定义可知   dp[1] = a[1]； dp[2] = max(a[1],a[2]);
4. 确定遍历顺序:dp[i] 是根据dp[i - 2] 和 dp[i - 1] 推导出来的，那么一定是从前到后遍历！
5. 举例推导dp数组:以输入[2,7,9,3,1]为例。

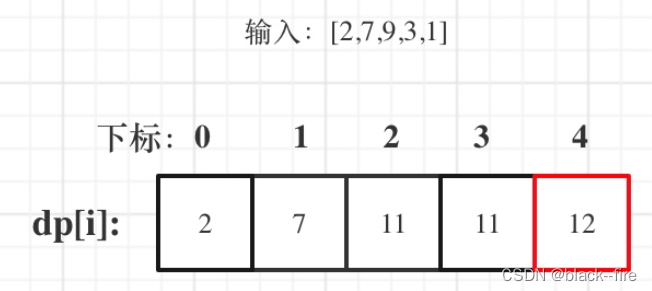
红框dp[n]为结果。

 代码如下:

#include <bits/stdc++.h>
using namespace std;
int n,a[100007],dp[100007],t;
int main()
{cin>>t;while(t--){memset(a,0,sizeof(a));memset(dp,0,sizeof(dp));cin>>n;for(int i = 1; i <= n; i++) cin>>a[i];dp[1] = a[1];dp[2] = max(a[1],a[2]);dp[3] = max(a[1] + a[3],a[2]);for(int i = 4; i <= n; i++) dp[i] = max((dp[i - 2] + a[i]),(dp[i - 3] + a[i - 1]));cout<<dp[n]<<endl;}return 0;
}

三，滚动数组优化

直接上代码,详见 动态规划之滚动数组_shaw chakong的博客-CSDN博客_动态规划滚动数组

#include <bits/stdc++.h>
using namespace std;
int n,a[100007],dp[5],t;
int main()
{cin>>t;while(t--){memset(a,0,sizeof(a));memset(dp,0,sizeof(dp));cin>>n;for(int i = 1; i <= n; i++) cin>>a[i];dp[1] = a[1];dp[2] = max(a[1],a[2]);for(int i = 3; i <= n; i++) dp[i % 4] = max((dp[(i - 2) % 4] + a[i]),(dp[(i - 1) % 4]));cout<<dp[n % 4]<<endl;}return 0;
}