核密度估计原理及sparkpython实现

核密度估计属于非参数估计，它主要解决的问题就是在对总体样本的分布未知的情况，如何估计样本的概率分布。
像平时，我们经常也会用直方图来展示样本数据的分布情况，如下图：

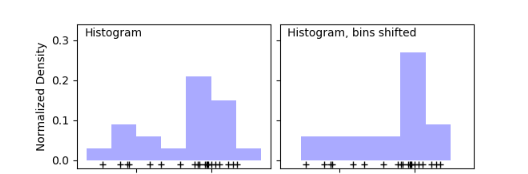
但是，直方图有着明显的缺点：

1. 非常不平滑，邻近的数据无法体现它们的差别；
2. 不同的bins画出的直方图差别非常大；
3. 无法计算概率密度值。

核密度估计

核密度估计就可以很好的解决直方图存在的问题，它的原理其实也很简单：当你需要估计一个点的概率密度值的时候，根据待估计点与每一个样本点的距离计算出一个密度值，距离越近，得到的密度值就越大，越远的话就越小，最后将所有密度值加权平均就得到该估计点在样本分布中的一个概率密度值了。
那为什么是这个原理呢？其实也很好理解，比如我们的该估计点处在样本点很密集的位置，不用算我们就自然就认为它的概率密度值也比较大。此时有许多样本点离待估计点很近，上面也说到离样本点的距离越近得到密度值就越大，那么也就意味着用于加权平均的密度值中有许多数值较大，算出来的最终密度值自然也会比较大。
具体公式如下：

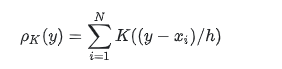
y是待估计点，xi就是样本点，i=1,2,…,N
K(x;h)是带有参数h的核函数，这里h的作用决定了核函数估计出来的分布的平滑程度，h越大，分布就会越平滑。

多维数据的核密度估计

对于多维数据，在计算密度值的时候，需要对每个维度的密度值进行累乘，具体公式如下：

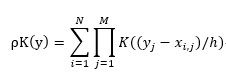
M就是数据的维度，y(j)是待估计点的第j维，x(i,j)是第i个样本点的第j维
但是，如果我们在对估计一个点的概率密度值的时候，如果将所有样本点都考虑进来计算的话，会非常的冗余。其实，我们可以就只考虑离待估计点比较相近的样本点，因为离得比较远的样本点，对该估计点的密度值贡献也非常小，甚至许多为0

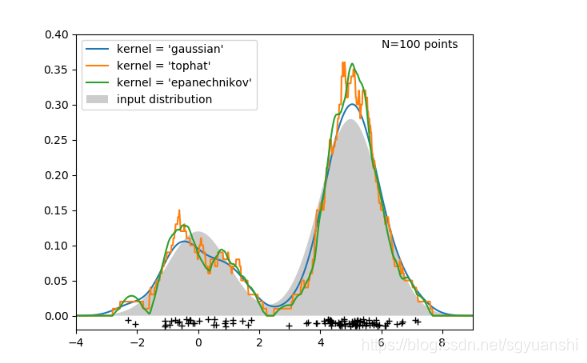
如上图，我们利用核密度估计对一个为双峰正态分布的样本进行估计，可以看出，通过核密度估计得到的分布于实际分布还是比较接近，也可以看出不同的核函数，估计出来的分布也是差别的。

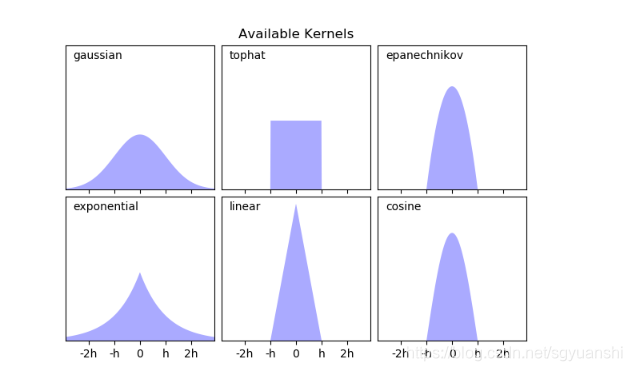
核函数

常见的函数主要有以下这些：

python实现

在python中实现核密度估计非常的简单，因为python已经提供了相关的API，直接调用就可以了。

from sklearn.neighbors.kde import KernelDensity
import numpy as np
X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
kde = KernelDensity(kernel='gaussian', bandwidth=0.2).fit(X)
kde.score_samples(X)array([-0.41075698, -0.41075698, -0.41076071, -0.41075698, -0.41075698,-0.41076071])

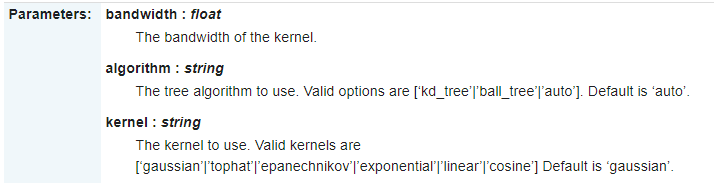
其中，最重要就是这三个参数了。bandwidth是上面公式中的h，algorithm就是加速邻近点的搜索算法如KD-Tree等，kernel就是核函数的选择了。

Spark实现

其实，spark也提供相应的api。

import org.apache.spark.mllib.stat.KernelDensityval sample = sc.parallelize(Seq(0.0, 1.0, 4.0, 4.0))
val kd = new KernelDensity().setSample(sample).setBandwidth(3.0)
val densities = kd.estimate(Array(-1.0, 2.0, 5.0))

但是呢，spark_mllib提供的核密度估计api只支持高斯分布的核函数，最重要的是它只支持一维数据，不支持多维数据的估计

spark多维核密度估计实现

在这里，我自己通过对源码的修改，实现了对多维数据的支持。

1. 首先，先修改setSample方法，让其能够接受多维的数据。

  /*** Sets the sample to use for density estimation.*/def setSample(sample: RDD[Array[Double]]): this.type = {this.sample = samplethis}/*** Sets the sample to use for density estimation (for Java users).*/def setSample(sample: JavaRDD[Array[Double]]): this.type = {this.sample = sample.rdd.asInstanceOf[RDD[Array[Double]]]this}

2. 接下来，就是修改estimate方法，即概率密度值估计的计算方法

  /*** Estimates probability density function at the given array of points.*/def estimate(points: Array[Array[Double]]): Array[Double] = {val sample = this.sampleval bandwidth = this.bandwidthrequire(sample != null, "Must set sample before calling estimate.")val n = points.length// This gets used in each Gaussian PDF computation, so compute it up frontval logStandardDeviationPlusHalfLog2Pi = math.log(bandwidth) + 0.5 * math.log(2 * math.Pi)val (densities, count) = sample.aggregate((new Array[Double](n), 0L))(// y是对sample的遍历// x是存放每次返回的Tuple，初始值即为传入的(new Array[Double](n), 0L)// 每次都将上一轮返回的x作为这一轮的x输入(x, y) => {var i = 0while (i < n) {var multiply:Double = 1for (m <- 0 until y.length) {multiply *= normPdf(y(m), bandwidth, logStandardDeviationPlusHalfLog2Pi, points(i)(m))}x._1(i) += multiplyi += 1}(x._1, x._2 + 1)},(x, y) => { // 这里是对所有分区的结果进行聚合blas.daxpy(n, 1.0, y._1, 1, x._1, 1)(x._1, x._2 + y._2)})blas.dscal(n, 1.0 / count, densities, 1)densities}
}

normPdf是计算正态分布概率密度值的一个静态类

private object KernelDensity {/** Evaluates the PDF of a normal distribution. */def normPdf(mean: Double,standardDeviation: Double,logStandardDeviationPlusHalfLog2Pi: Double,x: Double): Double = {val x0 = x - meanval x1 = x0 / standardDeviationval logDensity = -0.5 * x1 * x1 - logStandardDeviationPlusHalfLog2Pimath.exp(logDensity)}
}

完整代码

完整的代码比较长，我已经上传到GitHub，大家可以去仔细阅读。

欢迎关注同名公众号：“我就算饿死也不做程序员”。
交个朋友，一起交流，一起学习，一起进步。