本文主要是介绍高数 | 【极限与等价无穷小】两个重要极限 经典错误 什么情况下求极限可以直接带入,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
可以和这一篇配合食用。
高数 | 等价无穷小量的替换及加减替换条件_西皮呦的博客-CSDN博客_等价无穷小在加减中替换的条件?
可以结合网上等价无穷小是泰勒的粗糙版和 四则运算法中乘法的两个数的极限必须存在 来跟非零因子带入 对比来理解。
一、两个极限存在准则、两个重要极限
1、极限存在准则
夹逼定理(数列和函数极限都适用)、单调有界数列必收敛
对于第二条定理,当运用于函数时需要满足:趋近于无穷时,函数连续且处处有定义
例如:
若f(x)从某一X开始,当x>X时,在区间(x,+∞)满足f(x)连续且单调有界,则\lim_{x\rightarrow +\infty }f(x)存在。
注意哦,在某一区间连续的话那在该区间可一定是有定义的。
(-∞,X)的情况同理。
可以进一步思考,函数f(x)在某一点的极限只与该点领域内的函数值有关,与该点的函数值和离该点较远的函数值无关。
2. 第一个重要极限

□≠0


3. 第二个重要极限

需要说明的是,两个重要极限是通过两个极限存在准则推出来的。




4、经典的错误,标准的零分
首先 ,上方法。



这就是“经典的错误,标准的零分”

相当于无穷个无穷小的乘积!!所以不能用!!
这里再插一嘴:在求解类似于arctan、幂指数趋近于无穷时的极限时,要注意分别讨论+∞和-∞
如果有小伙伴说,那咱们让x趋近于+∞可以吗?
答案是:也不行!
如果x趋近于正无穷,那么乘积项的第二项极限不存在
同理,如果x趋近于负无穷,那么乘积项的第一项极限不存在
因此,就算的单边极限的情况下,求解这个极限也不可以使用重要极限。
常见错误总结:
5、经典的答案,标准的满分

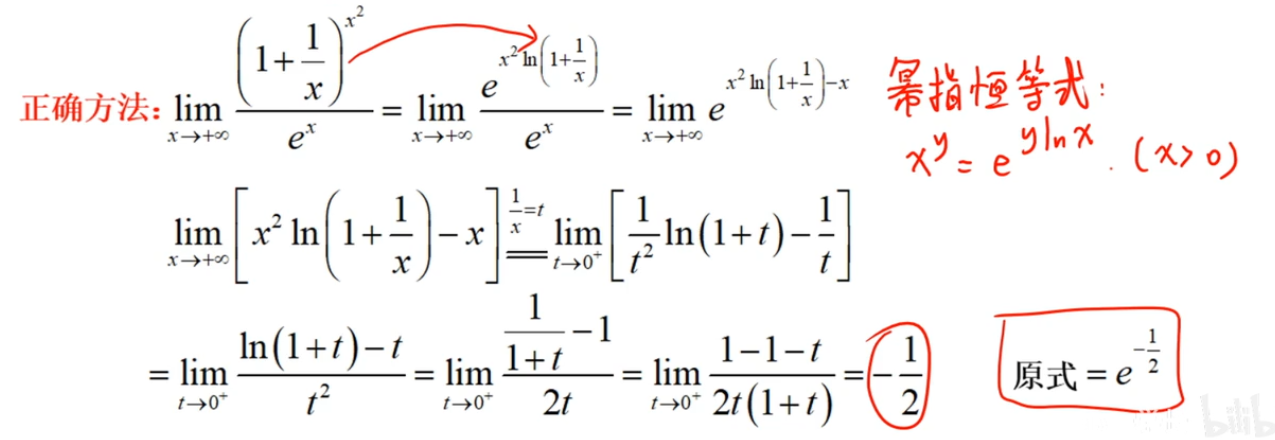
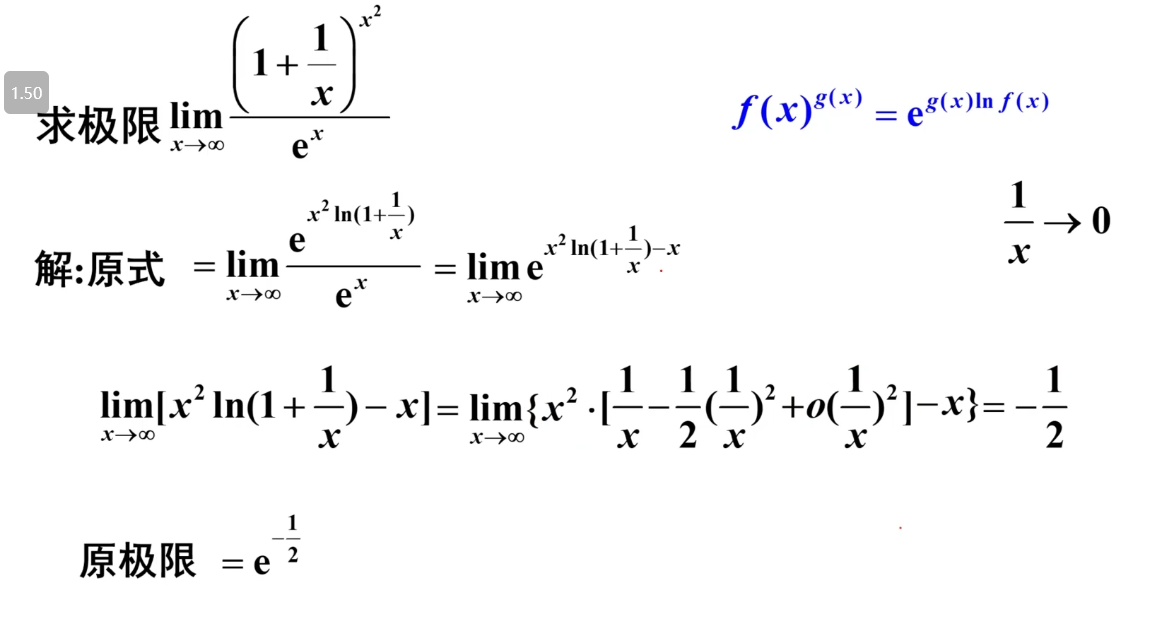
所以在遇到求解一个幂指数函数的极限时,化为底为常数e的指数函数,此时e对应于上式的f(x),满足大于0的条件,我们再只需求对应g(x)部分的极限即可。


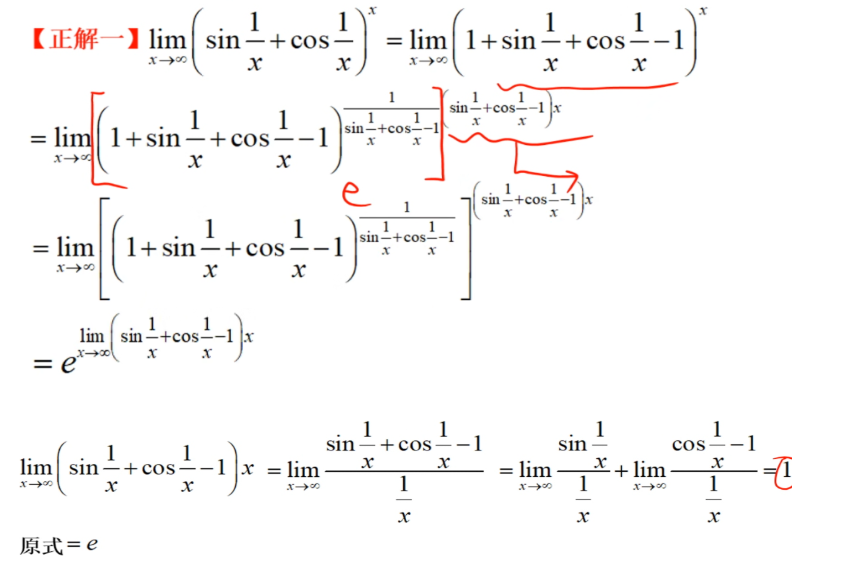

三. 导数定义式


四、计算极限常见错误

例题

1.一些随意等价替换的问题

2.随意代入值的问题

什么时候可以直接代入数字。
如果不是不定式,就能代。极限为∞时,仍然是属于定式。如果是不定式,就不能代。
中学概念的根深蒂固,会带来不利,例如:任何数的0次幂,等于1;1的任何次幂,都等于1。
在极限中这些概念要特别小心!极限中的0、1,不同于初等数学的0、1。
极限理论中的0、1,仅仅只是比喻而已。
只有整体乘项(整体除项)可以用等价替换,和非零常数极限先求。
能代入的一看有没有定义,二看是不是相乘或相除,即使是在因子上,如果代入之后是0或者∞(这个叫做未定式),也不能直接代入,得采用罗比达法则或者等价无穷小进一步运算。加减的除非拆项否则不可以代入。
注:未定式是高等数学中求极限中常见的问题,它不能直接代入计算。一共有7种。
分别是0比0,∞比∞,0*∞,1^∞,0^0,∞^0和∞-∞型。
未定式是指如果当x→x0(或者x→∞)时,两个函数f(x)与g(x)都趋于零或者趋于无穷大,那么极限lim [f(x)/g(x)] (x→x0或者x→∞)可能存在,也可能不存在,通常把这种极限称为未定式,也称未定型。未定式通常用洛必达法则求解
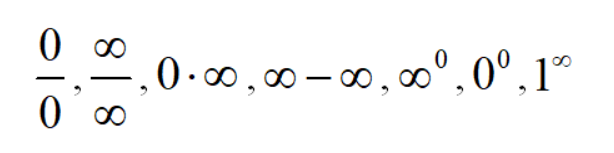
3.隐含四则运算的一个例子


那为什么对于红色的部分
不能愉快的直接令X=a呢?



全文见【高等数学】两个重要的极限 - 知乎
有关“重要极限”的经典例题_m0_53356029的博客-CSDN博客_两个重要极限典型错误
什么情况下求极限可以直接带入? - 知乎
这篇关于高数 | 【极限与等价无穷小】两个重要极限 经典错误 什么情况下求极限可以直接带入的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!











