圆内接四边形周长最大_解读【第59、60题】“将军饮马”之四边形周长或面积最（小）大...

关注“中考数学当百荟”，感谢您的点赞，转发！

一.回顾“将军饮马”问题

图1

将军饮马问题 如图1所示，将军从巡视点M点出发，走到河边l饮马后再回到营地N点，请问怎样走才能使总的路程最短？

解决策略分两步

第一步 先找出这个点；第二步 再证明这个距离最短。

第一步 先找出这个点

利用轴对称(镜面反射)，找点M关于直线l的对称点M’，连接M’N，M’N与l的交点O，即为所求，即此时OM＋ON最小(如图2)；

图2

第二步 为什么OM＋ON最小？

图3

思路 如图3，在直线l上任取异于点O的O’点，证明O’M＋O’N＞OM＋ON即可.

实操 在△O’M’N中，由两边之和＞第三边得，O’M’＋O’N＞M’N

由轴对称(镜面反射)性质得，M’N= OM’＋ON=OM＋ON

∴O’M＋O’N＞OM＋ON 得证

即点O即为所求.

二.解读每日一题59，60

每日一题59 实际可以转化为已知矩形邻边上的两个定点，在另外两边上分别求作两个点，使得这四点构成的四边形周长最小，即是应用该原理来完成的(如图4).

图4

每日一题60

60.如图5,在矩形PQRS中,PQ=3，PS=6.T，U，V三点分别在相邻三边上，且UT=UV=根号5，UT⊥UV,PU

图5

已知矩形三邻边上的三个定点(这三个定点有特殊的位置和数量关系)，分别求作一个点(该点与定点之间角度还有要求)，使得这四点构成的四边形面积最大，因而比每日一题59情况要复杂许多：除了轴对称外，还有隐圆问题。具体分析如下：

思路1 分三步达成

1.条件∠TWV＝45°，容易联想到90°的圆心角所对的圆周角为45°，而90°的圆心

角要充分利用题目已知TU＝UV，TU⊥UV来构造，即以U为圆心，UT为半径的⊙U；

2.作TV的中垂线，交⊙U于点W’， 点W’与U在TV的同侧，则圆心∠TUV＝90°

所对圆周角均为45°，即∠T W’V＝45°，且此时△T W’V的面积最大；

3.因为△TUV的面积=2.5，要使所求四边形面积最大，只需△WTV的面积最大，且点

W，U在TV的两侧.所以将△T W’V沿TV翻折，则点W’的对应点W即为所求(如图6)。

图6

思路2 分三步达成

1.条件∠TWV＝45°，容易联想到90°的圆心角所对的圆周角为45°，而90°的圆心角

要充分利用题目已知TU＝UV，TU⊥UV来构造，自然联想到以UT为边长的正方形了，

这可以通过作TV的中垂线，作圆1来构造正方形，其第四个顶点中垂线与圆1的交点；

2.要保证面积最大，再以正方形第四个顶点为圆心，边长为半径作圆2，则圆2与TV

中垂线的交点即为所求点W(如图7)。

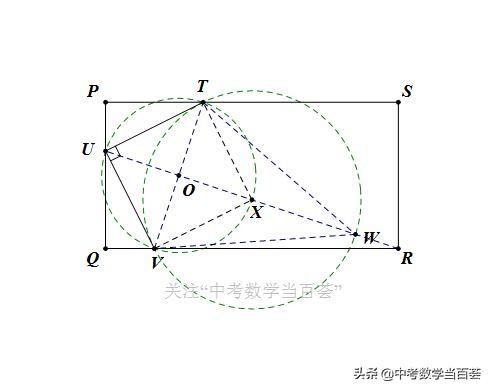
图7

3.然后通过计算判断点W的位置即最大面积。

按思路2计算

存在点W.理由如下：

∵TU＝UV＝根号5，∠P＝∠Q＝90°，∠PTU＋∠PUT＝∠QUV＋∠PUT＝90°，

∴∠PTU＝∠QUV，

在△PTU与△QVU中，

∠PTU＝∠QUV，∠P＝∠Q，TU＝UV，

∴△PTU≌△QVU，

∴PU＝QV，PT＝QU，设PU＝x，

则PT＝QU＝3－x，

∴x^2＋(3－x)^2＝5，

解得x＝1，x＝2(不合题意，舍去)，

∴PU＝QV＝1，QU＝PT＝2，

∴ST＝4，RV＝5，

连接TV，作TV的中垂线交TV于点O，以O为圆心，OT为半径画⊙O，交中垂线于

点X，则四边形TUVX是正方形，∠TXV＝90°，

以点X为圆心，以XT长为半径作⊙X，

要使∠TWV＝45°，且四边形WTUV面积最大，则点W既在⊙X上，又在VT的中垂线

上，因而⊙X与VT的中垂线的交点，即为所求点W.

∵TV＝根号10，∴XU＝TV＝根号10，

∵RT^2=TS^2＋SR^2=25，∴RT=RV=5，即R在VT的中垂线上；

∵RU＝2(根号10)，∴XR＝根号10，

∴XW＝XT＝UV＝根号5，∴XW＜XR，

∴点W在矩形PQRS的内部，

∴可以在矩形PQRS中，存在符合条件的面积最大的四边形TUVW.

最大面积＝1/2TV·UW＝根号10(根号10＋根号5)＝5＋2.5(根号2)≈8.54

关注“中考数学当百荟”，感谢您的点赞，转发！点击“了解更多”