本文主要是介绍如何理解Quadratic Weighted Kappa?,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Motivation
假定我们现在有 N N N个作文样例,以及它们对应的人类评分和GPT评分。评分一共有 C C C个互斥类别,分别是{0,1,2,3}。现在我们要衡量人类评分和GPT评分的一致性。
一个很直观的想法是,画出混淆矩阵,然后将对角线上的值汇总,除以总的样本数:
C o n s i s t e n c y h u m a n − G P T = N 人类评分 = G P T 评分 N 样本总数 Consistency_{human-GPT} = \frac{N_{人类评分=GPT评分}}{N_{样本总数}} Consistencyhuman−GPT=N样本总数N人类评分=GPT评分
这种计算方法没有考虑随机一致性。由于在分类任务中,有时两名评分者可能仅仅因为偶然而达成一致。下面引入的Cohen’s kappa指标,不仅仅考虑了观察到的一致性,而是通过考虑评分者随机达成一致的概率来调整这种一致性。
Cohen’s kappa:最基本的kappa统计
该指标用于衡量评分者之间的一致性。其值位于0和1之间,值越大说明一致性越高。下表解释了不同区间值所代表的一致性程度[1]:
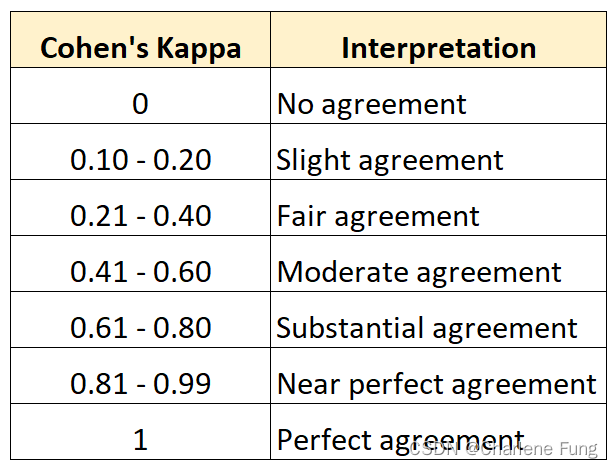
有如下定义:
κ = p o − p e 1 − p e = 1 − 1 − p o 1 − p e \kappa = \frac{p_o - p_e}{1 - p_e} =1-\frac{1 - p_o}{1 - p_e} κ=1−pepo−pe=1−1−pe1−po
其中,
p o p_o po: observed agreement,观察到的评分者间的一致性
p e p_e pe: chance agreement,假定的基于随机选择的评分者间一致性
可以看到,相比于原来的直接使用 p o p_o po来计算一致性,这里分子分母同时剔除了“随机一致性” p e p_e pe。
随机一致性的计算如下:
P 人类评分 = 0 = N 人类评分 = 0 N 样本总数 P_{人类评分=0} = \frac{N_{人类评分=0}}{N_{样本总数}} P人类评分=0=N样本总数N人类评分=0
P G P T 评分 = 0 = N G P T 评分 = 0 N 样本总数 P_{GPT评分=0} = \frac{N_{GPT评分=0}}{N_{样本总数}} PGPT评分=0=N样本总数NGPT评分=0
p e 人类评分 = G P T 评分 = 0 = P 人类评分 = 0 ∗ P G P T 评分 = 0 p_{e_{人类评分=GPT评分=0}} = P_{人类评分=0} * P_{GPT评分=0} pe人类评分=GPT评分=0=P人类评分=0∗PGPT评分=0
得到最终的随机一致性为:
p e = ∑ i C ( P 人类评分 = i ∗ P G P T 评分 = i ) p_e = \sum_i^C{(P_{人类评分=i} * P_{GPT评分=i})} pe=i∑C(P人类评分=i∗PGPT评分=i)
Weighted Kappa
Weighted kappa是Cohen’s kappa的扩展,特别适用于有序分类的情境。通过为每一对分类分配一个权重,可以根据不一致的严重性给予不同的惩罚。比如,评分0和3之间的不一致,大于1和2之间的不一致,那么应当给前者更重的惩罚。Quadratic Weighted Kappa,应用了平方权重,通常为分类间的距离的平方:
w i , j = ( i − j ) 2 ( C − 1 ) 2 w_{i,j} = \frac{(i-j)^2}{(C-1)^2} wi,j=(C−1)2(i−j)2
这里使用了归一化权重,分母用了 C − 1 C-1 C−1,是因为两个评分 i i i和 j j j的差异的最大值是 C − 1 C-1 C−1。如此,确保权重的范围在0到1之间。
κ = 1 − ∑ i , j w i , j O i , j ∑ i , j w i , j E i , j \kappa = 1- \frac{\sum_{i,j}{w_{i,j}O_{i,j}}}{\sum_{i,j}{w_{i,j}E_{i,j}}} κ=1−∑i,jwi,jEi,j∑i,jwi,jOi,j
(未完待续)
[1] 图片源自https://www.statology.org/cohens-kappa-statistic/
这篇关于如何理解Quadratic Weighted Kappa?的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






