1465. 切割后面积最大的蛋糕 : 为何仅需处理相邻切割位(多语言题解)

本文主要是介绍1465. 切割后面积最大的蛋糕 : 为何仅需处理相邻切割位(多语言题解)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目描述

这是 LeetCode 上的 「1465. 切割后面积最大的蛋糕」 ，难度为 「中等」。

Tag : 「贪心」、「模拟」

矩形蛋糕的高度为 h 且宽度为 w，给你两个整数数组 horizontalCuts 和 verticalCuts，其中：

horizontalCuts[i] 是从矩形蛋糕顶部到第 i 个水平切口的距离
verticalCuts[j] 是从矩形蛋糕的左侧到第 j 个竖直切口的距离

请你按数组 horizontalCuts 和 verticalCuts 中提供的水平和竖直位置切割后，请你找出「面积最大」的那份蛋糕，并返回其「面积」。

由于答案可能是一个很大的数字，因此需要将结果对取余后返回。

示例 1： alt

输入：h = 5, w = 4, horizontalCuts = [1,2,4], verticalCuts = [1,3]

输出：4 

解释：上图所示的矩阵蛋糕中，红色线表示水平和竖直方向上的切口。切割蛋糕后，绿色的那份蛋糕面积最大。

示例 2： alt

输入：h = 5, w = 4, horizontalCuts = [3,1], verticalCuts = [1]

输出：6

解释：上图所示的矩阵蛋糕中，红色线表示水平和竖直方向上的切口。切割蛋糕后，绿色和黄色的两份蛋糕面积最大。

示例 3：

输入：h = 5, w = 4, horizontalCuts = [3], verticalCuts = [3]

输出：9

提示：

题目数据保证 horizontalCuts 中的所有元素各不相同
题目数据保证 verticalCuts 中的所有元素各不相同

贪心

为了方便，记 horizontalCuts 为 hs，记 verticalCuts 为 vs。

由于求是“最大”蛋糕面积，「水平/垂直方向的连续段必然由「同方向且相邻」的切割位置（或是蛋糕边界）所构成」。

这点可通过反证法证明：如果最终蛋糕的（左右或上下）边缘不是由「相邻」的切割位置（或是蛋糕边界）决定，而是由跨越某些切割点的位置所决定的话，那么这个蛋糕必不是“完整”一块。

用题面的示例来举个 🌰，我们仅分析水平方向（hs = [1, 2, 4]）：

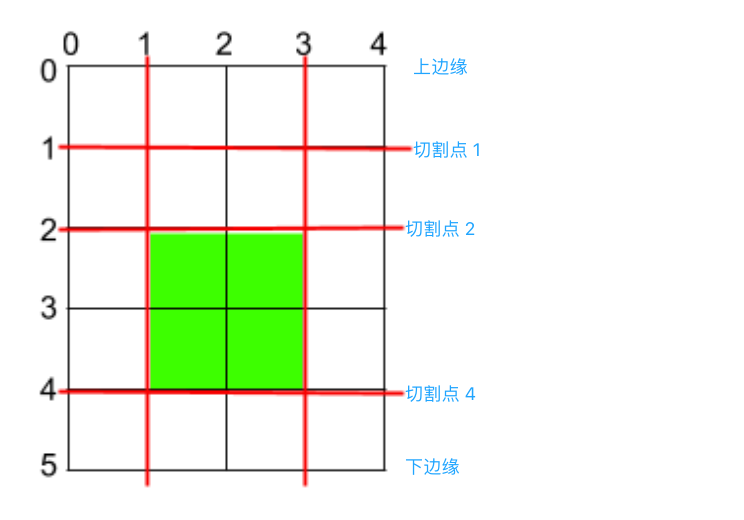
最终蛋糕的在该方向的连续段大小，只能是 [上边缘, 切割点 1]、[切割点 1, 切割点 2]、[切割点 2, 切割点 4] 和 [切割点 4, 下边缘] 四个之一，而不可能由非相邻切割点所组成，例如 [切割点 1, 切割点 4]（会被 切割点 2 所一分为二，不再完整）。

因此，我们可先对 hs 和 vs 进行排序，从而确保我们在遍历 hs 和 vs 过程中，处理到的均为「同反向且相邻」的切割位置。

随后，利用俩方向相互独立，分别求出俩方向连续段的最大长度，两者乘积即是答案。

Java 代码：

class Solution {
    int MOD = (int)1e9+7;
    public int maxArea(int h, int w, int[] hs, int[] vs) {
        Arrays.sort(hs);
        Arrays.sort(vs);
        int n = hs.length, m = vs.length;
        int mh = Math.max(hs[0], h - hs[n - 1]), mv = Math.max(vs[0], w - vs[m - 1]);
        for (int i = 1; i < n; i++) mh = Math.max(mh, hs[i] - hs[i - 1]);
        for (int i = 1; i < m; i++) mv = Math.max(mv, vs[i] - vs[i - 1]);
        return (int)((mh * 1L * mv) % MOD);
    }
}

Python 代码：

class Solution:
    def maxArea(self, h: int, w: int, hs: List[int], vs: List[int]) -> int:
        MOD = 10 ** 9 + 7
        hs.sort()
        vs.sort()
        n, m = len(hs), len(vs)
        mh, mv = max(hs[0], h - hs[n - 1]), max(vs[0], w - vs[m - 1])
        for i in range(1, n):
            mh = max(mh, hs[i] - hs[i - 1])
        for i in range(1, m):
            mv = max(mv, vs[i] - vs[i - 1])
        return (mh * mv) % MOD

C++ 代码：

class Solution {
public:
    int maxArea(int h, int w, vector<int>& hs, vector<int>& vs) {
        int MOD = 1e9+7;
        sort(hs.begin(), hs.end());
        sort(vs.begin(), vs.end());
        int n = hs.size(), m = vs.size();
        int mh = max(hs[0], h - hs[n - 1]), mv = max(vs[0], w - vs[m - 1]);
        for (int i = 1; i < n; i++) mh = max(mh, hs[i] - hs[i - 1]);
        for (int i = 1; i < m; i++) mv = max(mv, vs[i] - vs[i - 1]);
        return (mh * 1L * mv) % MOD;
    }
};

TypeScript 代码：

function maxArea(h: number, w: number, hs: number[], vs: number[]): number {
    const MOD = BigInt(1e9 + 7);
    hs.sort((a,b)=>a-b);
    vs.sort((a,b)=>a-b);
    const n = hs.length, m = vs.length;
    let mh = Math.max(hs[0], h - hs[n - 1]), mv = Math.max(vs[0], w - vs[m - 1]);
    for (let i = 1; i < n; i++) mh = Math.max(mh, hs[i] - hs[i - 1]);
    for (let i = 1; i < m; i++) mv = Math.max(mv, vs[i] - vs[i - 1]);
    return Number((BigInt(mh) * BigInt(mv)) % MOD);
};