求全排列的两种方法（Java）

递归法

假设我们有0，1，2，3四个数需要全排列，递归法是一种比较类似于深度搜索的方法，直到递归最深处，才得出结果。

其大概思路是，设置一个游标start，游标所到之处，其左侧已经考虑过，利用递归思想求剩下的全排列。

仔细分析，依次考虑每一位数。由于对于每一位数，它可能的数包括除了之前考虑过的所有数，因此将start右侧（包括start）的所有数都和start这一位交换一次，每交换后，马上进入递归函数（start+1），接着再执行一次原交换，用于复原。这样就做成了把每一个数都在这个位上排列一次，递归函数的调用表示对剩下的数进行全排列。

代码如下：

package main;public class Main {static int[] a = {0, 1, 2, 3};static int result = 0;public static void main(String[] args) {dfs(0);System.out.println("The total of all permutation of a[] is: " + result);}public static void dfs(int start) {if (start >= a.length) {System.out.print(a[0]);for (int i = 1; i < a.length; i++) {System.out.print(", " + a[i]);}System.out.println();result++;return;}for (int i = start; i < a.length; i++) {swap(start, i);dfs(start + 1);swap(start, i);}}public static void swap(int i, int j) {int temp = a[i];a[i] = a[j];a[j] = temp;}
}

给出输出结果：

回溯法

这种方法叫回溯法，他的思想也是用到递归的思想，长得也和上面递归法很像，只是从递归函数的解读来说，和递归法还是有区别的。（leetcode上经常有回溯法求解的题）

在回溯法中，通常有多个辅助变量：待选列表或集合，已选列表或集合，表示结果的列表或集合，等等。其递归思想，就是

1. 每次遍历待选
2. 更新表示结果的列表或集合
3. 更新已选列表或集合
4. 执行递归操作
5. 恢复表示结果的列表或集合，恢复已选列表或集合。

这么看来，好像是和递归法没什么区别。我的理解是，递归法和回溯法本质上都是递归，在求全排列问题上，递归解法和回溯法极其相似，但是在一些应用问题中，用递归法不是那么好理解，而回溯法的思考模式和我们人想问题差不多，递归套路就是挨个试，因此回溯法还是比较容易接受的。

还有一点要注意的是，在全排列问题上，回溯法用的复杂度较高，效率低于递归法。

下面附上代码：

package main;import java.util.ArrayList;
import java.util.HashSet;
import java.util.List;
import java.util.Set;public class Main {static int[] a = {0, 1, 2, 3};static Set<Integer> all = new HashSet<Integer>(); // 全体集合（待选集合=全体集合-已选集合）static Set<Integer> used = new HashSet<Integer>(); // 已选集合static List<List<Integer>> resultList = new ArrayList<>(); // 全局结果列表public static void main(String[] args) {for (int i = 0; i < a.length; i++) {all.add(a[i]);}backtrack(0, new ArrayList<Integer>());System.out.println("The total of all permutation of a[] is: " + resultList.size());}public static void backtrack(int p, List<Integer> tempresult) {if (p >= a.length) {System.out.print(tempresult.get(0));for (int i = 1; i < tempresult.size(); i++) {System.out.print(", " + tempresult.get(i));}System.out.println();resultList.add(tempresult);return;}for (Integer n : all) {if (!used.contains(n)) {used.add(n);tempresult.add(n);backtrack(p + 1, tempresult);tempresult.remove(tempresult.size() - 1);used.remove(n);}}}public static void swap(int i, int j) {int temp = a[i];a[i] = a[j];a[j] = temp;}
}

执行结果：

执行结果对比

比较上面两个方法中，输出执行结果的区别，发现：

在递归法中：

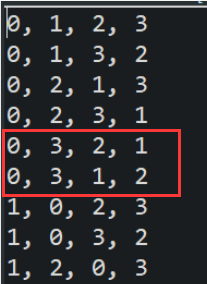
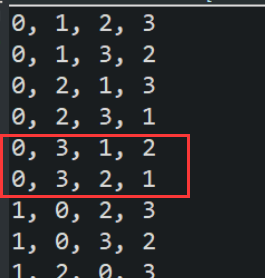
回溯法中：

由于两种方法（尽管都用到了递归）对递归含义的解释，也就是执行思路不同，导致了结果输出顺序的不同。

在递归法中，先输出0321，后输出0312，是因为此时正在考虑第二位（start=1），已经对这一位考虑过了数字1和数字2，现在需要将数字3和原本的1做交换，而这个操作和数字2无关，所以数字2还在它原来的位置上。直到考虑第三位时（start=2），才与后面的1交换，输出了0321.

在回溯法中，先输出0312，后输出0321，这是因为，在集合的遍历中，由于对集合all的遍历顺序实际上是字典序（数字从小到大），因此这就好比我们人的思维模式，逐位考虑可能的数字，而考虑的顺序就是字典序了。这样最后输出的全排列顺序，也是字典序。

谢谢！