本文主要是介绍Additive Powers-of-Two (APoT) Quantization:硬件友好的非均匀量化方法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Additive Powers-of-Two Quantization:硬件友好的非均匀量化方法
- 摘要
- 方法
- Additive Powers-of-Two量化 (APoT)
- 量化表示
- 均匀量化表示
- Powers-of-Two (PoT) 量化表示
- Additive Powers-of-Two(APoT)量化表示
- 参数化Clipping函数 (RCF)
- 权重归一化
- APoT量化伪代码
- 实验结果
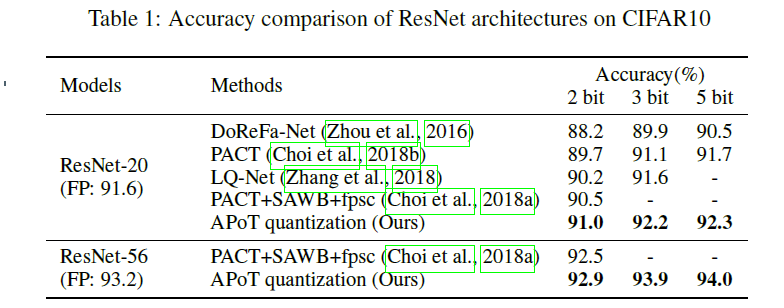
- CIFAR-10
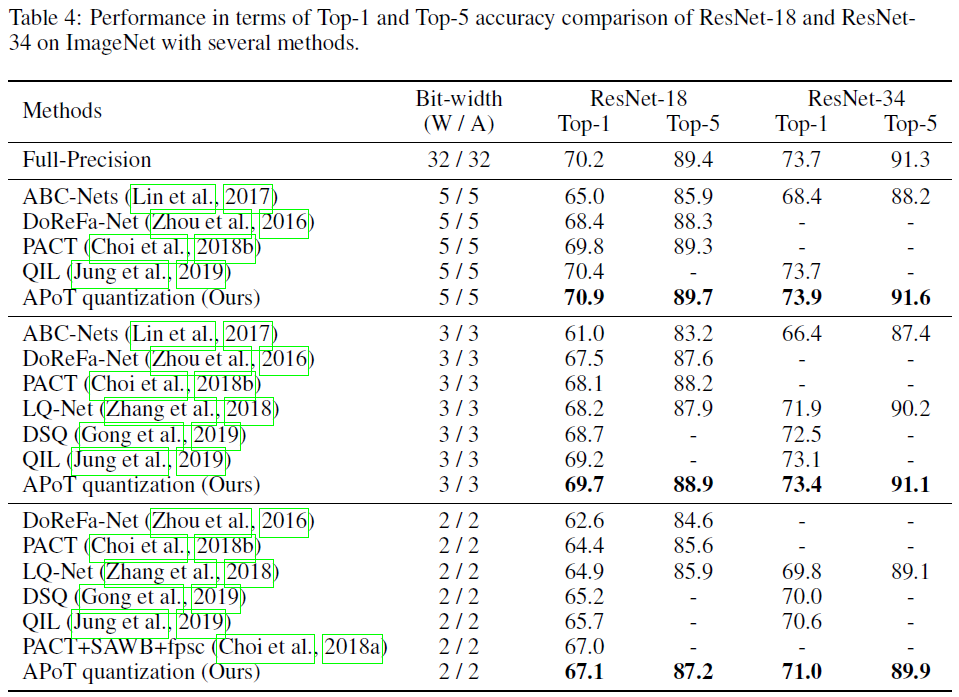
- ImageNet
本文是电子科大&哈佛大学&新加坡国立联合发表在 ICLR2020 上的一篇非均匀量化(APoT)的工作。本文,在非均匀量化中通过采用Additive Powers-of-Two(APoT)加法二次幂量化,综合考虑了计算上有效性,低比特量化导致的模型精度下降问题。并实现了不错的量化效果!
- 论文题目:Additive Powers-of-Two Quantization: A Non-uniform Discretization for Neural Networks
- 论文链接:https://arxiv.org/pdf/1909.13144v2.pdf
- 论文代码:https://github.com/yhhhli/APoT_Quantization
摘要
本文首先提出了Additive Powers-of-Two(APoT)加法二次幂量化,一种针对钟形和长尾分布的神经网络权重,有效的非均匀性量化方案。通过将所有量化数值限制为几个二次幂相加,这APoT量化有利于提高计算效率,并与权重分布良好匹配。其次,本文通过参数化Clipping函数以生成更好的更新最佳饱和阈值的梯度。最后,提出对权重归一化来调整权重的输入分布,使其在量化后更加稳定和一致。实验结果表明,本文提出的方法优于最先进的方法,甚至可以与全精度模型竞争,因此证明了本文提出的APoT量化的有效性。例如,本文在 ImageNe t上的 3bit 量化 ResNet-34 仅下降了 0.3% 的 Top-1 和 0.2% Top-5 的准确性。
方法
Additive Powers-of-Two量化 (APoT)
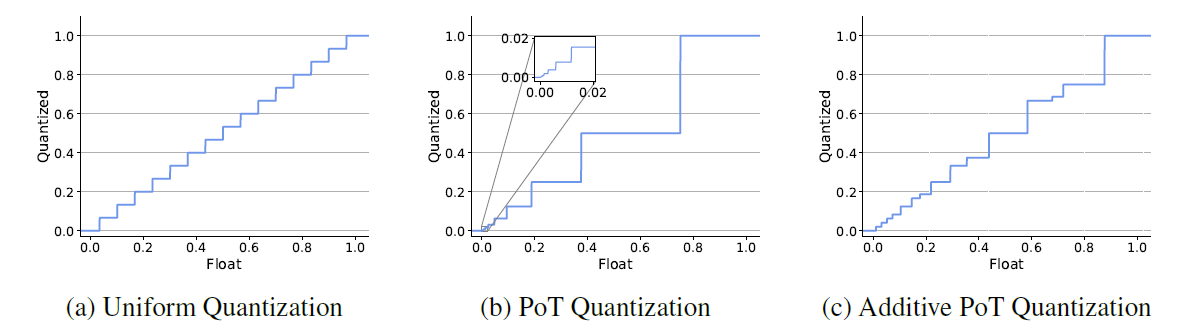
量化表示
W ^ = Π Q ( α , b ) ⌊ W , α ⌉ \hat{\boldsymbol{W}}=\Pi_{\mathcal{Q}(\alpha, b)}\lfloor\boldsymbol{W}, \alpha\rceil W^=ΠQ(α,b)⌊W,α⌉
- W ∈ R C out × C in × K × K \boldsymbol{W} \in \mathbb{R}^{C_{\text {out}} \times C_{\text {in}} \times K \times K} W∈RCout×Cin×K×K
- α \alpha α 代表裁剪阈值。
- ⌊ ⋅ , α ⌉ \lfloor \cdot , \alpha\rceil ⌊⋅,α⌉ 代表Clip函数,将权重裁剪到 [ − α , α ] [-\alpha, \alpha] [−α,α]。
- W \boldsymbol{W} W中每个元素通过 Π ( ⋅ ) \Pi(\cdot) Π(⋅) 映射成量化值
- Q ( α , b ) \mathcal{Q}(\alpha, b) Q(α,b)代表量化候选数值
- b b b 代表量化位宽
均匀量化表示
Q u ( α , b ) = α × { 0 , ± 1 2 b − 1 − 1 , ± 2 2 b − 1 − 1 , … , ± 1 } \mathcal{Q}^{u}(\alpha, b)=\alpha \times\left\{0, \frac{\pm 1}{2^{b-1}-1}, \frac{\pm 2}{2^{b-1}-1}, \ldots,\pm 1\right\} Qu(α,b)=α×{0,2b−1−1±1,2b−1−1±2,…,±1}
Powers-of-Two (PoT) 量化表示
Q p ( α , b ) = α × { 0 , ± 2 − 2 b − 1 + 1 , ± 2 − 2 b − 1 + 2 , … , ± 2 − 1 , ± 1 } \mathcal{Q}^{p}(\alpha, b)=\alpha \times\left\{0, \pm 2^{-2^{b-1}+1}, \pm 2^{-2^{b-1}+2}, \ldots, \pm 2^{-1},\pm 1\right\} Qp(α,b)=α×{0,±2−2b−1+1,±2−2b−1+2,…,±2−1,±1}
基于Powers-of-Two (PoT) 的非均匀量化模式有一个好处是在计算过程中可以采用移位的方式代替复杂的乘法运算,因此幂次的非均匀量化可以显著提高计算效率。如下公示所示:
2 k x = { x if k = 0 x < < k if k > 0 x > > k if k < 0 2^{k} x=\left\{\begin{array}{lr} x & \text { if } k = 0 \\ x << k & \text { if } k > 0 \\ x >> k & \text { if } k < 0 \end{array}\right. 2kx=⎩⎨⎧xx<<kx>>k if k=0 if k>0 if k<0
基于Powers-of-Two (PoT) 的非均匀量化十分适配基于钟型的weights形式,可以实现0附近权重集中的位置量化表示多,长尾部分量化表示少。
Additive Powers-of-Two(APoT)量化表示
PoT 量化虽然十分适配基于钟型的weights形式,但是,对于增加bit数是没有明显增益。比如,我们将位宽从 b b b设置为 b + 1 b+1 b+1时 [ 0 , ± 2 − 2 b − 1 + 1 ] \left[0, \pm 2^{-2^{b-1}+1}\right] [0,±2−2b−1+1]范围内的间隔(interval)不会发生变化,只是在 [ − 2 − 2 b − 1 + 1 , 2 − 2 b − 1 + 1 ] \left[-2^{-2^{b-1}+1}, 2^{-2^{b-1}+1}\right] [−2−2b−1+1,2−2b−1+1]范围进一步缩小间隔。这个问题被定义为 rigid resolution(刚性分辨率)问题。为解决此问题,本文提出了APoT量化表示。
Q a ( α , k n ) = γ × { ∑ i = 0 n − 1 p i } where p i ∈ { 0 , 1 2 i , 1 2 i + n , … , 1 2 i + ( 2 k − 1 ) n } \mathcal{Q}^{a}(\alpha, k n)=\gamma \times\left\{\sum_{i=0}^{n-1} p_{i}\right\} \text { where } p_{i} \in\left\{0, \frac{1}{2^{i}}, \frac{1}{2^{i+n}}, \ldots, \frac{1}{2^{i+\left(2^{k}-1\right) n}}\right\} Qa(α,kn)=γ×{i=0∑n−1pi} where pi∈{0,2i1,2i+n1,…,2i+(2k−1)n1}
- γ \gamma γ 是一个缩放系数,以确保 Q a \mathcal{Q}^{a} Qa 中的最大级别是 γ \gamma γ。
- k k k 称为基位宽,即每个加法项的位宽, n n n 是加法项的数量。
- 当设置了位宽 b b b和基位宽 k k k时, n n n可由 n = b k n=\frac{b}{k} n=kb计算得到。
参数化Clipping函数 (RCF)
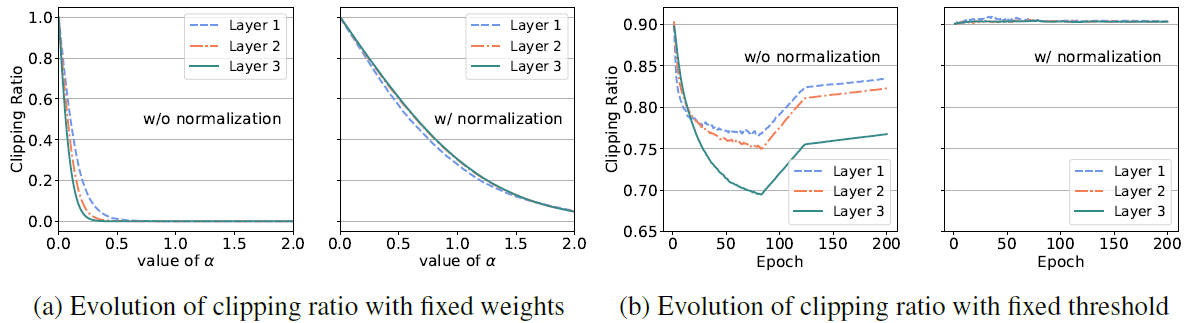
传统的STE仅仅对clip函数边界以外的阈值梯度值进行更新,对于边界以内的阈值参数梯度均为零,这不利于寻找最优的clip阈值边界。
∂ W ^ ∂ α ≈ ∂ ⌊ W , α ⌉ ∂ α = sign ( W ) if ∣ W ∣ > α else 0 \frac{\partial \hat{W}}{\partial \alpha} \approx \frac{\partial\lfloor W, \alpha\rceil}{\partial \alpha}=\operatorname{sign}(W) \text { if }|W|>\alpha \text { else } 0 ∂α∂W^≈∂α∂⌊W,α⌉=sign(W) if ∣W∣>α else 0
针对传统STE梯度约束不完整的问题,本文对权重内外的阈值边界梯度均进行梯度约束,以便于更快更好的训练得到最优阈值。
W ^ = α Π Q ( 1 , b ) ⌊ W α , 1 ⌉ \hat{\boldsymbol{W}}=\alpha \Pi_{\mathcal{Q}(1, b)}\left\lfloor\frac{\boldsymbol{W}}{\alpha}, 1\right\rceil W^=αΠQ(1,b)⌊αW,1⌉
∂ W ^ ∂ α = { sign ( W ) if ∣ W ∣ > α Π Q ( 1 , b ) W α − W α if ∣ W ∣ ≤ α \frac{\partial \hat{\boldsymbol{W}}}{\partial \alpha}=\left\{\begin{array}{ll} \operatorname{sign}(\boldsymbol{W}) & \text { if }|\boldsymbol{W}|>\alpha \\ \Pi_{\mathcal{Q}(1, b)} \frac{\boldsymbol{W}}{\alpha}-\frac{\boldsymbol{W}}{\alpha} & \text { if }|\boldsymbol{W}| \leq \alpha \end{array}\right. ∂α∂W^={sign(W)ΠQ(1,b)αW−αW if ∣W∣>α if ∣W∣≤α
class _pq(torch.autograd.Function):@staticmethoddef forward(ctx, input, alpha):input.div_(alpha) # weights are first divided by alphainput_c = input.clamp(min=-1, max=1) # then clipped to [-1,1]sign = input_c.sign()input_abs = input_c.abs()if power:input_q = power_quant(input_abs, grids).mul(sign) # project to Q^a(alpha, B)else:input_q = uniform_quant(input_abs, b).mul(sign)ctx.save_for_backward(input, input_q)input_q = input_q.mul(alpha) # rescale to the original rangereturn input_q@staticmethoddef backward(ctx, grad_output):grad_input = grad_output.clone() # grad for weights will not be clippedinput, input_q = ctx.saved_tensorsi = (input.abs()>1.).float()sign = input.sign()grad_alpha = (grad_output*(sign*i + (input_q-input)*(1-i))).sum()return grad_input, grad_alpha
权重归一化
权重归一化为裁剪(Clip)和投影(projection)提供了相对一致且稳定的输入分布,这便于在训练过程中更平滑地优化不同层和迭代。 此外,将权重的平均值设为零可以使得量化更加对称。权重归一化公式如下,主要是通过权重值减均值除方差完成,使得归一化后的权重分布满足均值为0方差为1。
W ~ = W − μ σ + ϵ , where μ = 1 I ∑ i = 1 I W i , σ = 1 I ∑ i = 1 I ( W i − μ ) 2 \tilde{\boldsymbol{W}}=\frac{\boldsymbol{W}-\mu}{\sigma+\epsilon}, \text { where } \mu=\frac{1}{I} \sum_{i=1}^{I} \boldsymbol{W}_{i}, \sigma=\sqrt{\frac{1}{I} \sum_{i=1}^{I}\left(\boldsymbol{W}_{i}-\mu\right)^{2}} W~=σ+ϵW−μ, where μ=I1i=1∑IWi,σ=I1i=1∑I(Wi−μ)2
APoT量化伪代码

实验结果
CIFAR-10
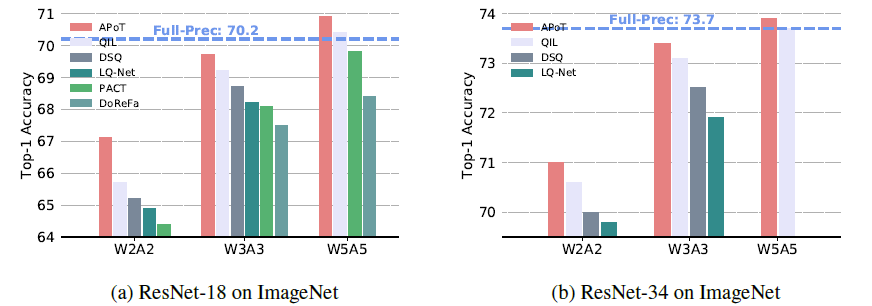
ImageNet

这篇关于Additive Powers-of-Two (APoT) Quantization:硬件友好的非均匀量化方法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




