本文主要是介绍管理类联考——逻辑——知识篇——形式逻辑——六、假言——haimian,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
假言
考点分析
| 年度 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | 2023 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 题量 | 10 | 6 | 3 | 12 | 4 | 6 | 13 | 4 | 5 |
定义分类
假言命题是断定一全事物情况的存在是另一个事物情况存在的条件的命题,又称条件命题。假言命题可以分为三类:充分条件假言命题、必要条件假言命题、充要条件假言命题。
- 充分条件假言命题
(1)符号:A→B,读作:A推 B。
(2)逻辑含义:如果A为真,则B一定为真。也称A是B的充分条件。
(3)常用连接词:
(4)推理关系:充分条件前推后。 - 必要条件假言命题
(1)符号:B→A,读作:B推A。
(2〉逻辑含义:A对于B来说是不可缺少的条件,没有条件A,就不会产生B,这个结果。反之,如果B为真,则A一定为真,也称A是B的必要条件。
(3)常用连接词:
(4)推理关系:必要条件后推前 - 充要条件假言命题
(1)符号:A ←→ B,读作:A当且仅当B。
(2)逻辑含义:如果A为真,则B一定为真;如果B为真,A一定为真;反之,如果A为假,则B一定为假;如果B为假,则A一定为假;即A是B的充分条件,也是B的必要条件即A是B的充分必要条件。
(3)常用连接词:
(4)推理关系
定义分类1
分成:充分、必要和充要
- 充分条件
【定义】若P为真时,Q必然为真,则称P是Q的充分条件。【本质】充分条件的本质是有之即可,无之不定。
【典例】如果考上研究生,那么参加了考试。
【分析】若考上了研究生,则必然推出参加了考试。反之,若没有考上研究生,则可能参加了考试,也可能根本没有参加考试。因此考上研究生是参加考试的充分条件。 - 必要条件
【定义】若Q为假时,P必然为假,则称Q是P的必要条件。【本质】必要条件的本质是无之不可,有之不定。
【典例】不参加考试就考不上研究生。
【分析】如果不参加考试就不可能考上研究生,但是参加考试也不一定能考上研究生。 - 充要条件
【定义】若P真时Q真,Р假时Q假,则称P和Q互为充要条件。
【本质】充要条件的本质就是二者等价,即二者总是同时成立或者同时不成立。
推理关系
-
充分、必要与P→Q型假言命题
传统的形式逻辑体系会区分充分型假言命题和必要型假言命题。理论上二者自然是有区别的,但是实际上只需要从应试的角度出发知道推理关系即可。
例如,“如果考上研究生,那么参加了考试”和“不参加考试就考不上研究生”的意思是基本相同的。
【定义】充分条件Р和必要条件Q之间的推理关系就是P→Q型假言命题。
【刻画】充分条件和必要条件之间的推理关系统一刻画为P→Q。其中P就是充分条件,通常被简称为前件;Q就是必要条件,通常被简称为后件。
从应试的角度来看,我们一般根据指示词去识别和刻画P → Q型假言命题。 -
充要与P ←→ Q型假言命题
【定义】若P和Q互为充要条件,则二者的推理关系为Р ←→ Q型假言命题。P ←→ Q型假言命题也叫充要型假言命题P ←→ Q。
从应试的角度来看,我们一般根据指示词去识别P ←→ Q型假言命题。
指示词语
P→Q型假言命题的指示词
从应试的角度来看,我们一般根据指示词去识别和刻画P → Q型假言命题。
常见词
| 指示词 | 典例 | 刻画结果 |
|---|---|---|
| 如果P,那么Q | 如果考上,那么要努力 | 考上→要努力 |
| 一P,就Q | 一学逻辑,就觉得自己很理性 | 学逻辑→觉得自己很理性 |
| 若P,则Q | 若你安好,则是晴天 | 你安好→是晴天 |
| P,必须Q | 想脱单,必须考上研究生 | 脱单→考上研究生 |
| Q是P的基础 | 爱情是婚姻的基础 | 婚姻→爱情 |
| Q是P的前提 | 热量有缺口是减肥的前提 | 减肥→热量有缺口 |
| 只有Q,才P | 只有长得帅,才有资格犯错误 | 有资格犯错误→长得帅 |
| 不Q,不P | 不思考,就学不会逻辑 | 学会逻辑→思考 |
特殊词
在指示词中,“除非”的问题比较特殊,故在此单独总结。
【公式】除非A,否则B = A,否则B = B,除非A = A或B = ┐A → B = ┐B → A。
【口诀】除非与否则,一假推另真;缺除非补除非,缺否则补否则。
“除非否则等于或”的意思是看到除非否则的结构可以直接变成“或”,然后利用相容选言命题的推理性质得到推理关系。当然大家熟练之后,可以直接写出推理结果。
“缺除非补除非,缺否则补否则”的意思是如果只有一个单独的“否则”就补上“除非”,如果只有一个单独的“除非”就补上“否则”。例如,“A,否则B”=“除非A,否则 B"。
【公式】除非B,才A = 若A,除非B =A→B。
这个公式的记忆很简单,只要把“除非”等同于“只有”即可。
从应试的角度来看,我们一般根据指示词去识别P ←→ Q型假言命题。
P ←→ Q型假言命题的指示词
| 指示词 | 典例 | 刻画结果 |
|---|---|---|
| 当且仅当 | 我喜欢你,当且仅当她是她 | 我喜欢你 ←→ 她是她 |
| 唯一标准 | 效率高是备考质量高的唯一标准 | 效率高 ←→ 备考质量高 |
推理性质
传统的形式逻辑体系会区分充分型假言命题和必要型假言命题。理论上二者自然是有区别的,但是实际上只需要从应试的角度出发知道推理关系。即充分、必要与P→Q型假言命题,充要与P ←→ Q型假言命题。
P→Q的推理性质
若已知“如果考上,那么通过了国家线”,我们不难得到如下四条结论:
①若考上,那么通过了国家线。
②若没有通过国家线,那么没考上。
③如果没考上,那么可能通过国家线,也可能没有通过国家线。
④如果通过了国家线,那么可能考上,也可能没考上。
根据指示词“如果,那么”,我们可将原判断刻画为“考上→通过了国家线",其中“考上”就是前件,“通过了国家线”就是后件。因此,我们可以得到如下口诀。
【口诀】P→Q的推理,前真后真,后假前假,前假后不定,后真前不定。
P ←→ Q的推理性质
由于P ←→ Q的本质含义是P、Q等价,故其中一个为真时另一个必然为真,其中一个为假时另一个也必然为假。因此,我们可以得到如下口诀。
【口诀】P ←→ Q的推理,一真另真,一假另假。
思维导图
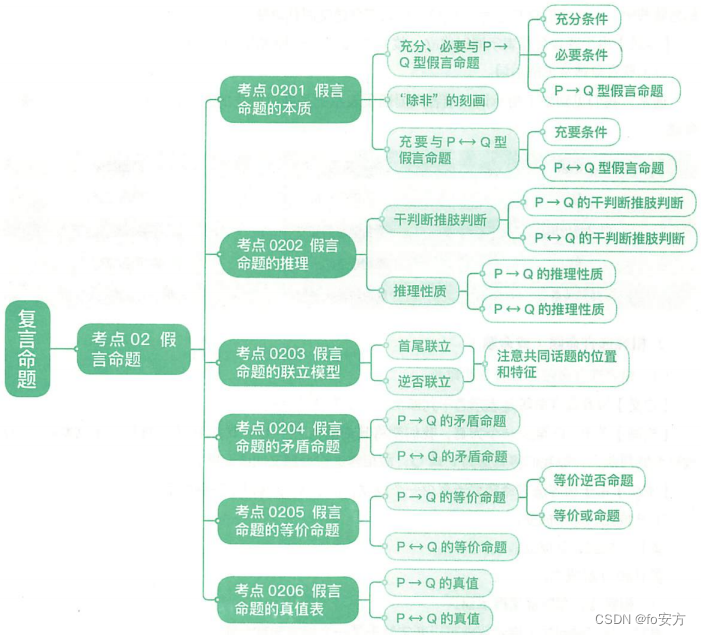
推理规则
- 逆否规则:A → B = ┐B → ┐A
- 传递规则:A → B,B → C,可得A → B → C。
重要关系
矛盾关系
公式:A → B与 A ∧ ┐B是矛盾关系
题型
等价变形
推理规则
矛盾关系
真话假话
结构相似

这篇关于管理类联考——逻辑——知识篇——形式逻辑——六、假言——haimian的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







