Artifacts 瑕疵，频率方面的基础知识，傅里叶变换，卷积 ，从频率的角度看采样，减少走样的方法,深度缓存 Z-Buffer

Artifacts 瑕疵

在计算机图形学中Artifacts（瑕疵）指的是Errors / Mistakes / Inaccuracies

采样产生的Artifacts

锯齿

摩尔纹

Moire Pattterns（去掉图像的奇数行和奇数列）—— 由欠采样undersampling造成

产生Artifacts 的原因

很多Artifact产生的原因是信号变换太快而采样太慢

一种反走样的方法 —— 在采样之前做模糊（滤波）

对原始的信号做模糊（滤波）再进行采样即可进行反走样。（注意：顺序不能变，先采样再模糊无法反走样）

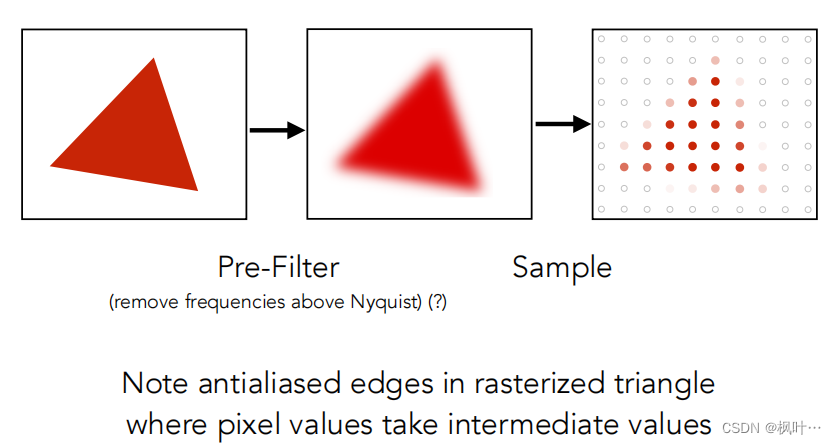
频率方面的基础知识

频域 Frequency Domain

频域是描述信号在频率方面特性时用到的一种坐标系。 在电子学，控制系统工程和统计学中，频域图显示了在一个频率范围内每个给定频带内的信号量 。

频率和周期

频率是f，周期是T。
频率越快，函数变化越快，如下图所示。

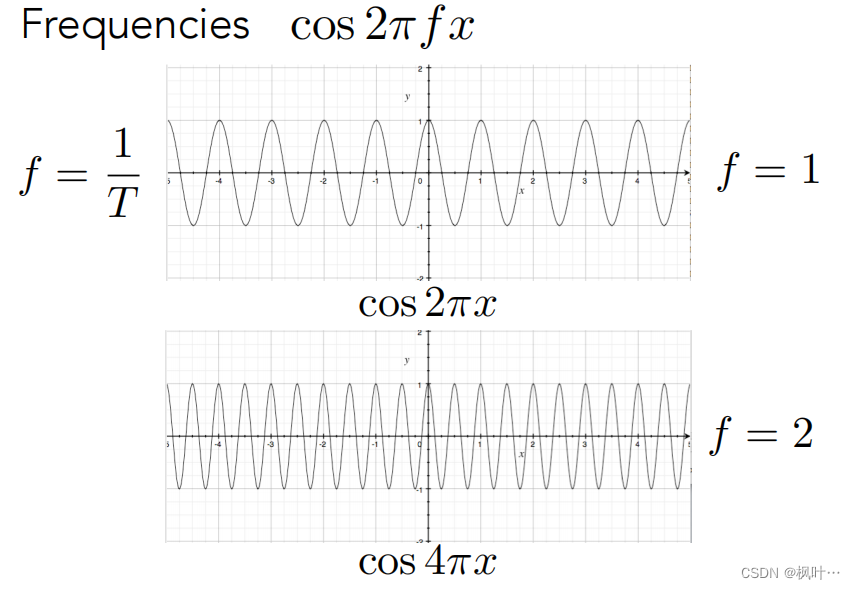
傅里叶变换

傅里叶级数展开

一切函数都可以写成一系列正弦函数和余弦函数的线性组合与一个常数项。任何函数分解为频率从低到高的若干函数。

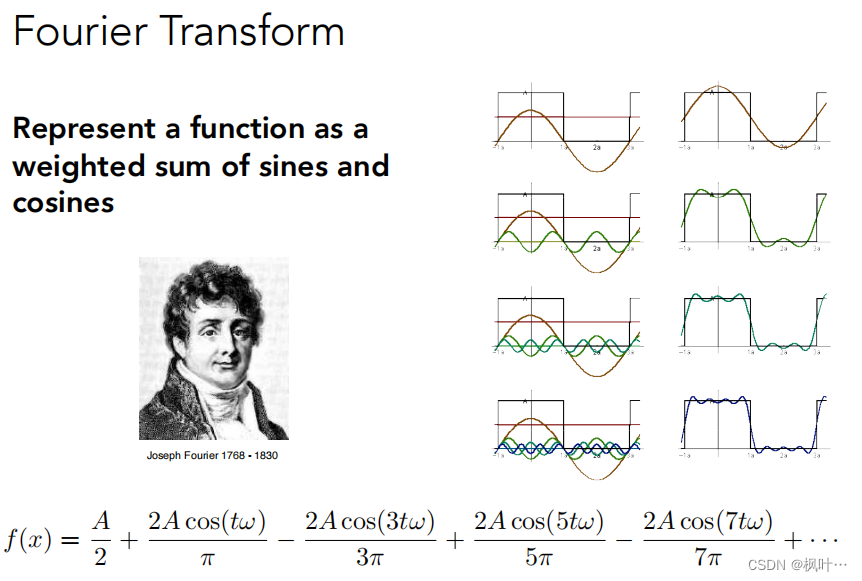
傅里叶变换

下面展示了傅里叶变换和逆傅里叶变换。

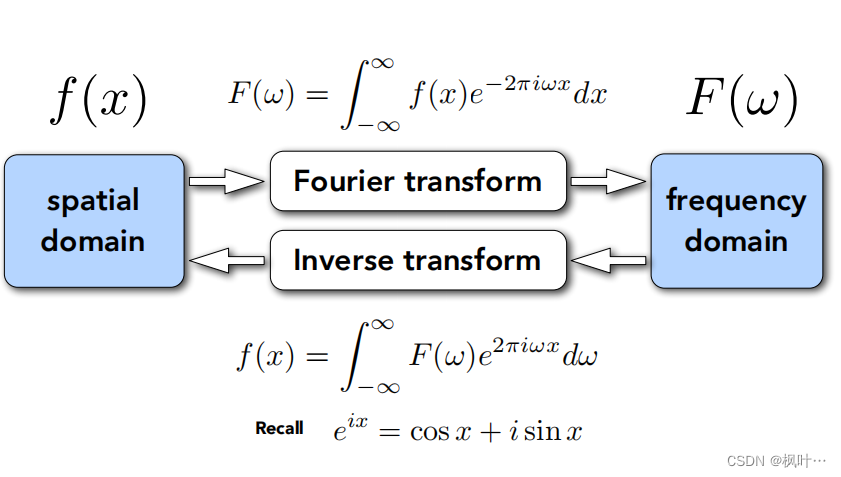
从频率图像上来分析走样

频率越高的函数，采样回复到原函数的效果越差。即：高频率需要更快的采样。


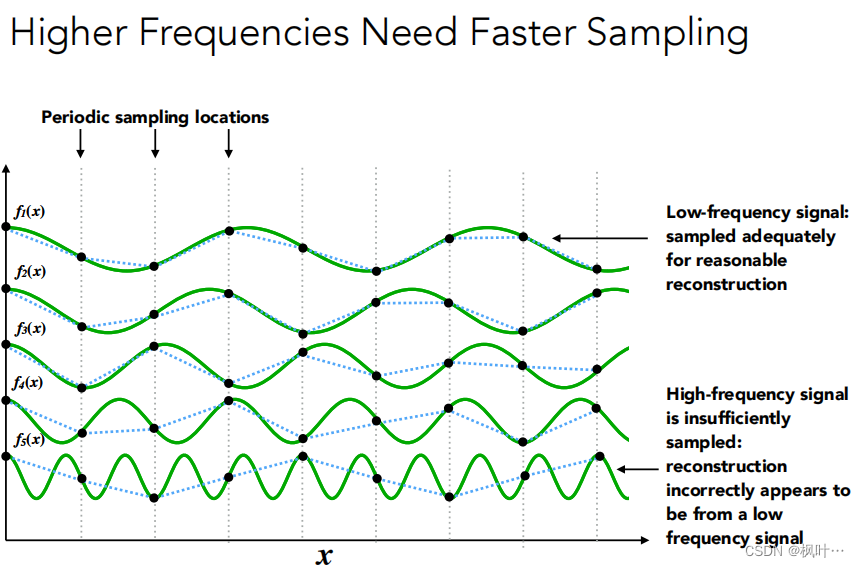
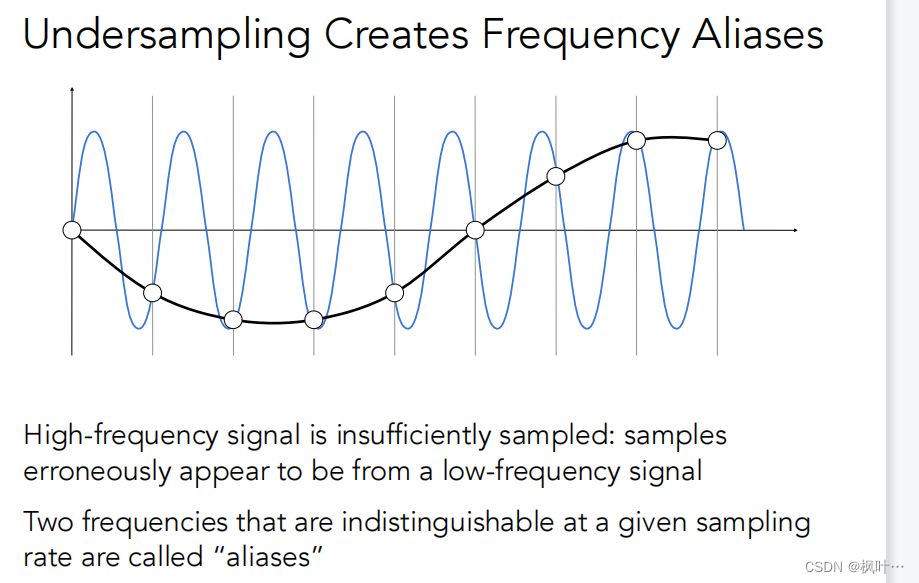
走样：从频率分析角度定义走样：同样的采样方法采样两种频率的函数，但是得出的结果无法区分。

滤波

（频率角度上）滤波就是去掉一系列的频率。

傅里叶变化的作用

傅里叶变换可以把图像从时域变到频域。对下左图进行傅里叶变换，得到下右图。下右图中，中心是低频区域，向外延伸，频率越来越高，为高频区域。亮度代表信息密度，区域越亮表示信息越集中，下图表示图片的大多数信息都处于低频。右下图右成为频谱。

高通滤波（High-pass filter）

消除低频的信号，只让高频信号可以通过，再使用逆傅里叶变换得到图像。

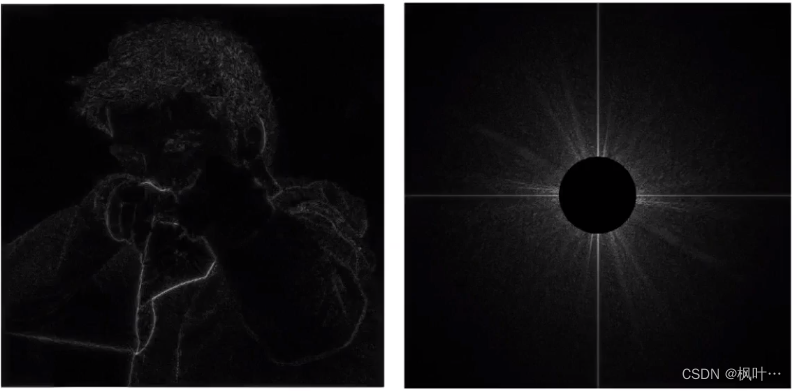
边界的特点：图像中发生突变的位置（颜色差的很多）。对应信号变换特别大，频率大，所有高通滤波器显示边界。

低通滤波/模糊（Low-pass filter/Blur）

消除高频的信号，只让低频信号可以通过，然后进行逆傅里叶变换。

低筒滤波器消除边界，让图片变得模糊。

带通滤波（Band-pass filter）

去掉高频和低频的信息，然后进行逆傅里叶变换。

卷积 Convolution

滤波 Filtering = 卷积 Convolution （= 平均 Averaging）
卷积是多个变量在某范围内相乘后求和的结果。
简单理解：有一个滑动窗口（滤波器），窗口的每个格子有权重，将这个窗口在信号上从左向右滑动做点乘。如下图所示。

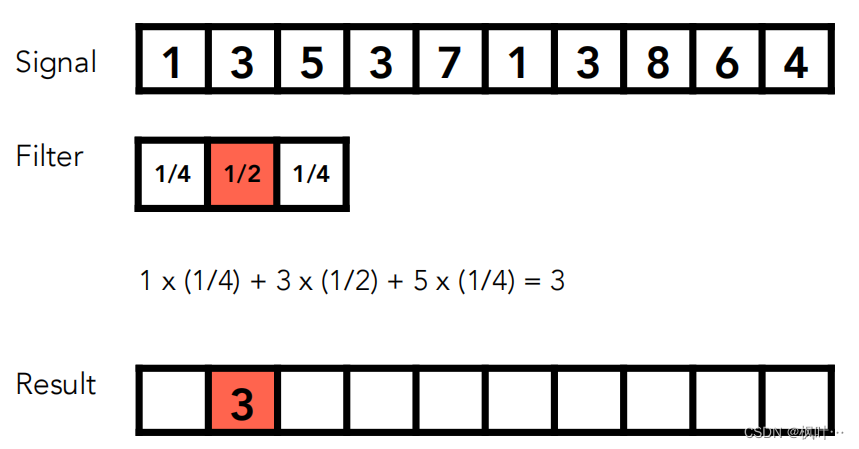
卷积定理 Convolution Theorem

卷积定理指出，函数卷积的傅立叶变换是函数傅立叶变换的乘积。
具体分为时域卷积定理和频域卷积定理，两者具有对偶关系。

卷积定理的应用

如下图所示上面一行图片是时域的卷积(*是卷积操作）下面一行图片是频域的乘积。

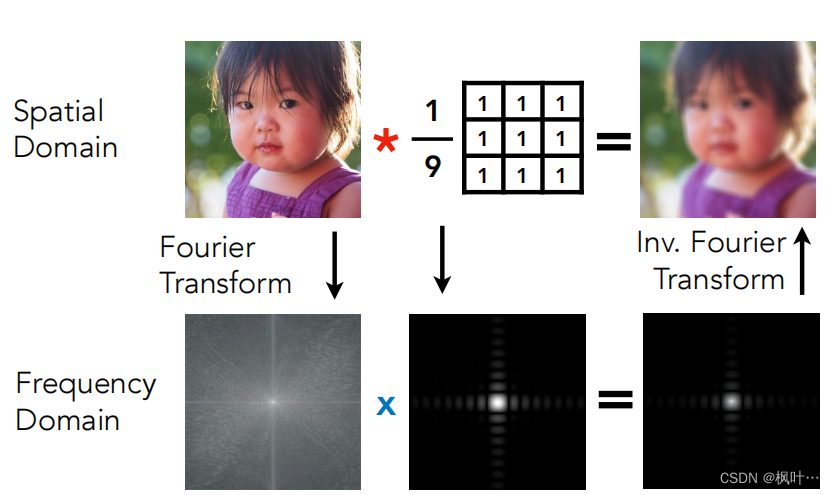
卷积中的低通滤波器

下面盒子形状的滤波器（Box Filter）就是低通滤波器。

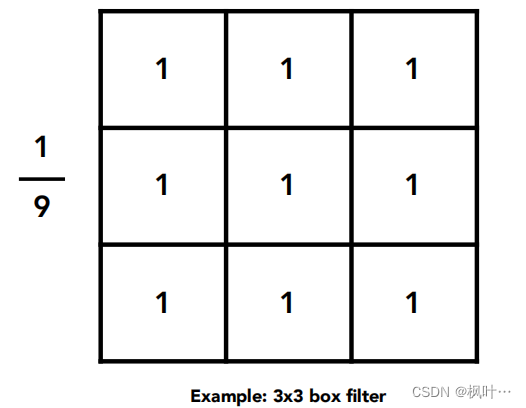
乘上1/9是为了卷积后的图片颜色与原来基本一致，否则图片就太亮了（归一化）。

卷积核大小与频率的关系

越小的box，留下频率种类越多。


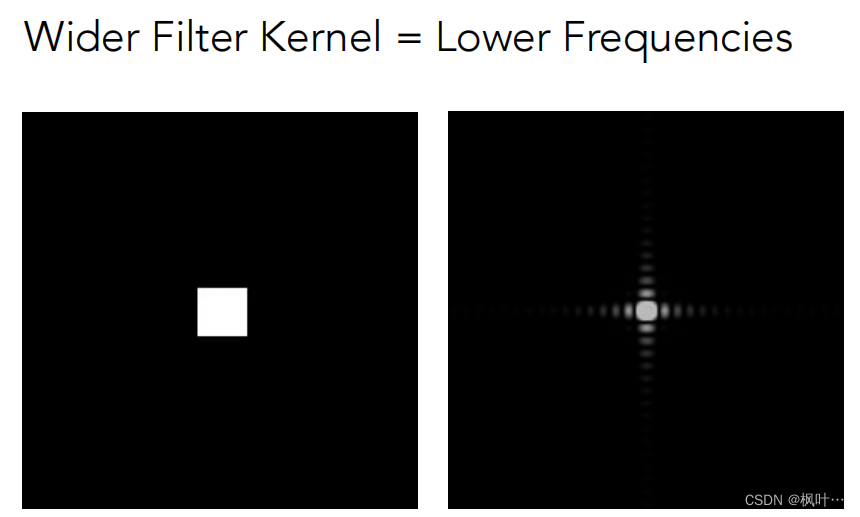
越大的box，留下越低的频率，结果更加模糊。

从频率的角度看采样

采样就是重复频域上的内容。

冲激函数

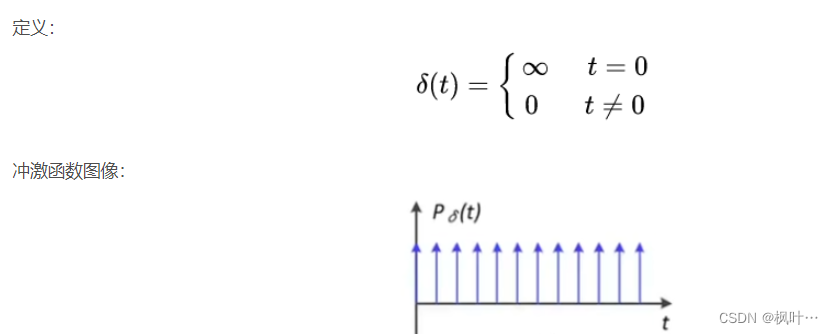
获得采样（与冲激函数相乘）

对于原始信号a，让它与冲激函数相乘，就可以得到采样的结果。

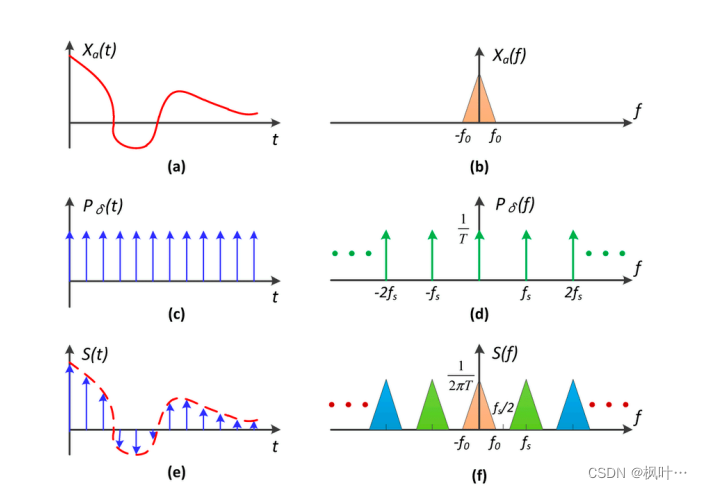
**采样就是重复原始信号的频谱。**采样就是将原始信号粘贴了一份。

走样 = 频谱在搬移后出现了混合 Aliasing=Mixed Frequency Contents

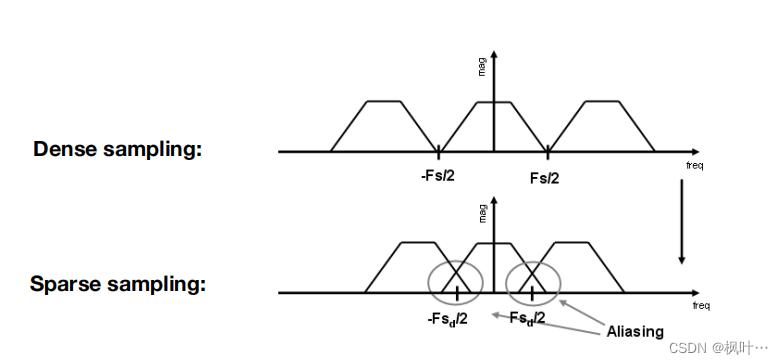
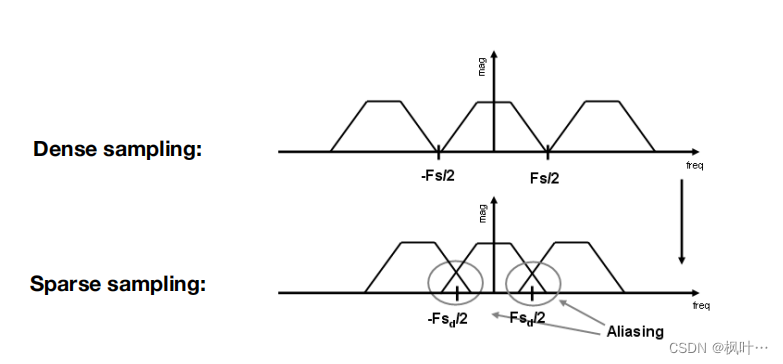
走样的原因是：在频谱的角度，原始信号在复制粘贴时出现了信号的重叠。

减少走样的方法

增加采样率

可以使用高分辨率的显示器、传感器、帧缓冲器。

进行反走样

不是通过提高分辨率抗锯齿。
反走样简单来说就是：在对频谱重复之前，先让频谱更窄，减少信号的重叠。即先去掉一些的高频信息，然后再采样。这就解释了为什么模糊一个图像后采样能够抗走样。，如下图所示。

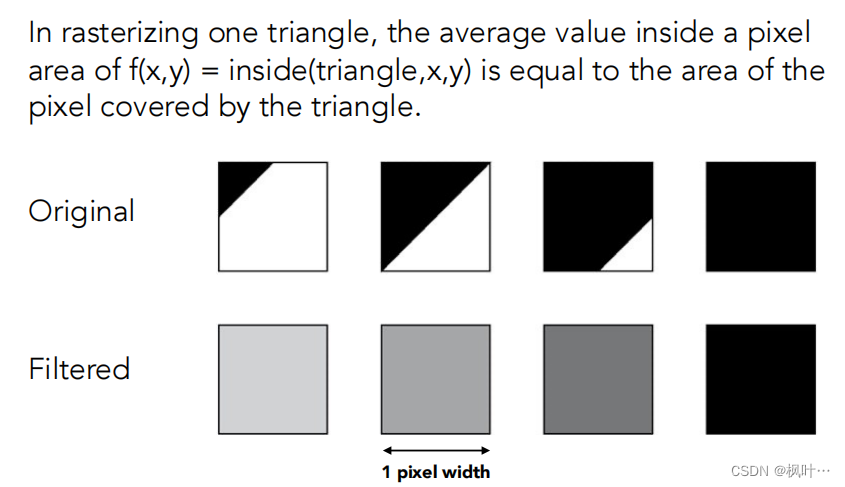
如何模糊三角形—通过在像素区域平均来反走样

使用一个低通滤波器，针对每个像素做卷积操作，然后对每个像素中心进行采样。

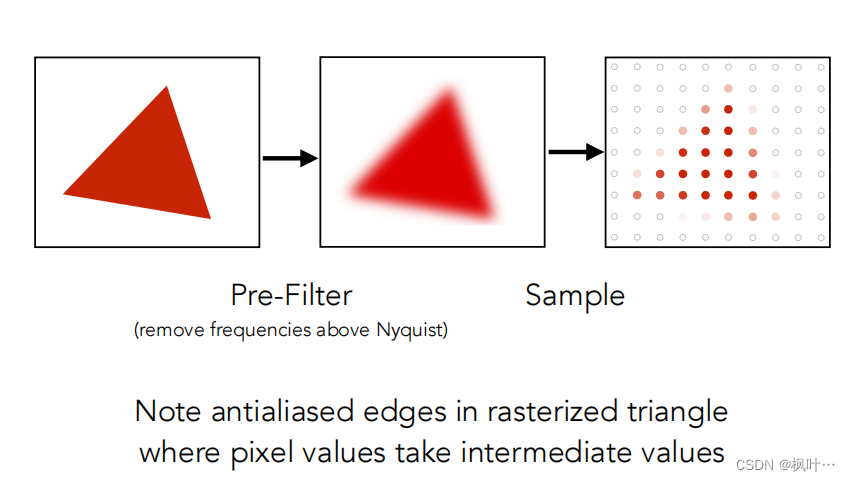
像素区域的亮度等于覆盖的图案覆盖这个像素的面积（即把像素内部的值平均起来）

多重采样 Antialiasing By Supersampling（MSAA）

我们通过在一个像素内划分出更多的中心点来用更多的采用点进行反走样，将一个划分多个像素，判断这些更小的像素点是否在三角形内部，统计在三角形内部小像素点的个数判断覆盖率，但注意这只是反走样的近似，并不能真正解决反走样问题。

超采样 Supersampling

第一步：对每个像素划分N × N的采样点。

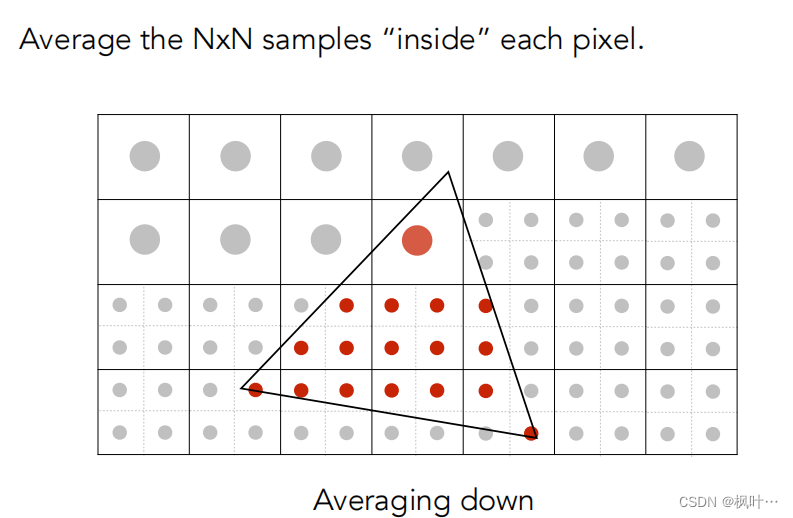
第二步：在每个像素里对这个N × N的采样点做平均。

结果：

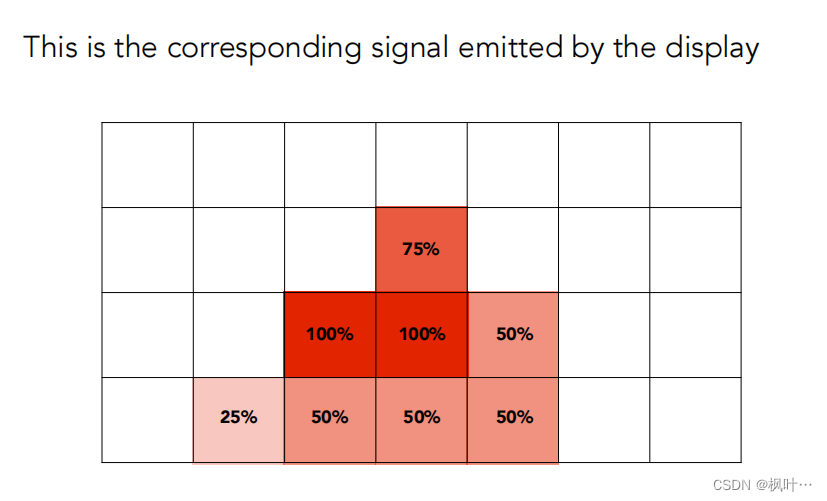
抗锯齿了：

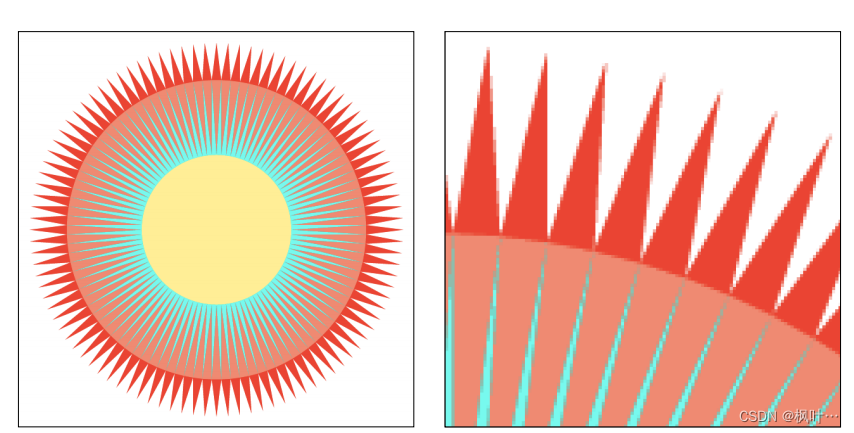
这种方法增大了计算量实现抗锯齿。

其他抗锯齿的方法

FXAA（Fast Approxiamate AA）：先获得有锯齿的图，然后找到边界，然后将有锯齿的边界替换成没有锯齿的边界。
TAA（Temporal AA）：复用上一帧感知到的结果，相当于把MSAA的样本分布到时间上，然后不对当前这一帧引入额外的操作。

超分辨率问题 Super resolution / super sampling

• 超分辨率就是从低分辨率到高分辨率（比如把256 × 256图片拉大到1024 × 1024）
• 本质上仍是采样不足的问题，与抗锯齿的问题相似。
• 可以采用DLSS（Deep Learning Super Sampling）的方法，利用深度学习猜出来。

可见性 / 遮挡 Visiblity / occlusion

画家算法 Painter’s Algorithm

思想：首先绘制距离较远的场景，然后用绘制距离较近的场景覆盖较远的部分。
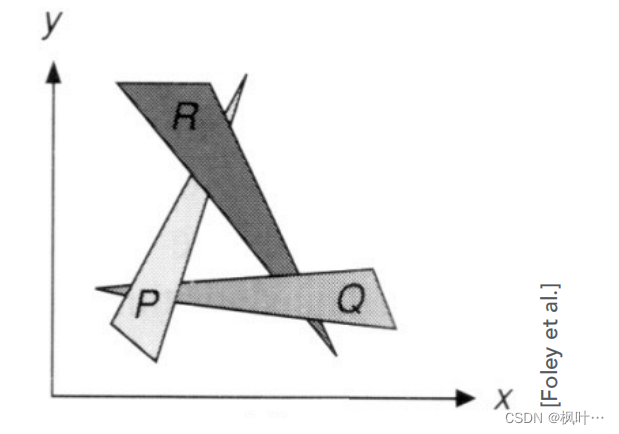
存在的问题：首先画家算法需要按照深度排序需要将物体按照深度进行排序，但是对于以下三个三角形，无法确定深度的顺序，所以实际上我们无法使用画家算法。

深度缓存 Z-Buffer

1. 存储每个像素当前最小的z值（深度值）
2. 需要一个额外的缓存来存储深度值

• frame buffer 存储颜色值
• depth buffer（z-buffer）存储深度值（为了简化，我们假设所有z都是正数，z越小越近）
  
  上述两张图同步生成，左边的图实际渲染，右边的是深度缓存图，离我们近颜色越深，反之离我们越远。

Z-Buffer 算法

1. 初始化深度缓存为无限大
2. 在光栅化时，有：
   
   例子：