【使用维纳滤波进行信号分离】基于维纳-霍普夫方程的信号分离或去噪维纳滤波器估计（Matlab代码实现）

本文主要是介绍【使用维纳滤波进行信号分离】基于维纳-霍普夫方程的信号分离或去噪维纳滤波器估计（Matlab代码实现），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

维纳滤波器是一种常用的信号处理技术，可用于信号分离和去噪。基于维纳-霍普夫方程的维纳滤波器是一种理想滤波器，旨在最小化原始信号与滤波器输出之间的误差。

在信号分离或去噪任务中，我们有一个观测信号y，它可以被表示为原始信号s和加性噪声n的叠加：y = s + n。维纳滤波器的目标是找到一个滤波器h，使得滤波器的输出y' = h * y能够近似地估计原始信号s。

根据维纳-霍普夫方程，最优的维纳滤波器可以通过以下形式计算得到：

h = (P_ss * H^T) * (H * P_ss * H^T + P_nn)^(-1)

其中，H是观测信号y的转置矩阵，P_ss是原始信号s的自相关矩阵，P_nn是噪声n的自相关矩阵（通常被假设为对角矩阵）。

维纳滤波器的输出可以通过以下方式得到：

y' = h * y = (P_ss * H^T) * (H * P_ss * H^T + P_nn)^(-1) * y

通过将观测信号y代入上式，我们可以得到分离或去噪后的信号估计值y'。

需要注意的是，维纳滤波器的性能受到观测信号的统计特性以及原始信号和噪声的自相关性质的影响。因此，在使用维纳滤波器进行信号分离或去噪时，需要对信号和噪声的统计特性有一定的了解，并相应地选择合适的参数和技术。此外，维纳滤波器可能对信号的频谱产生一定的改变，因此在实际应用中需要仔细考虑这一点。

📚2 运行结果

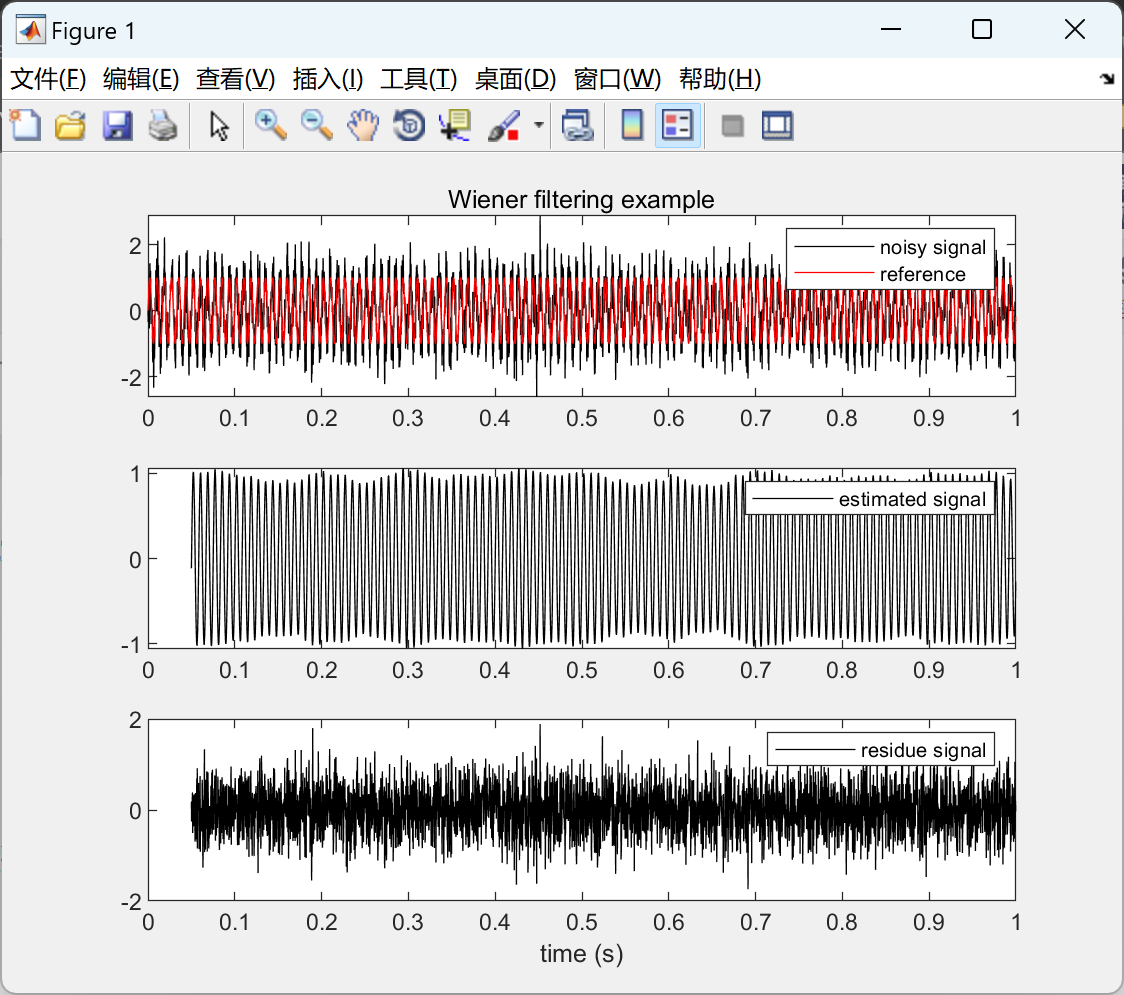
部分代码：

function [xest,B,MSE] = wienerFilt(x,y,N)
%
% Wiener filter based on Wiener-Hopf equations
% This function takes as inputs a noisy signal, x, and a reference signal, y,
% in order to compute a N-order linear filter that provides an estimate of y
% from x
%
% INPUTS
% x = noisy signal
% y = reference signalsinit
% N = filter order
%
% OUTPUTS
% xest = estimated signal
% b = Wiener filter coefficents
% MSE = mean squared error
%

X = 1/N .* fft(x(1:N));
Y = 1/N .* fft(y(1:N));
X = X(:);
Y = Y(:);

Rxx = N .* real(ifft(X .* conj(X))); % Autocorrelation function
Rxy = N .* real(ifft(X .* conj(Y))); % Crosscorrelation function
Rxx = toeplitz(Rxx);
Rxy = Rxy';
B = Rxy / Rxx; B = B(:); % Wiener-Hopf eq. B = inv(Rxx) Rxy
xest = fftfilt(B,x);
xest = xest(N+1:end); % cut first N samples due to distorsion during filtering operation
MSE = mean(y(N+1:end) - xest) .^2; % mean squared error