东方博宜OJ 【基础】卒的遍历

题目描述

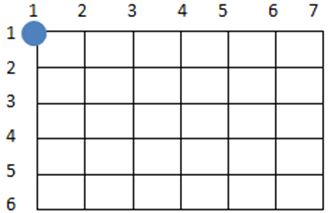
在一张n*m的棋盘上（如6行7列）的最左上角（1,1）的位置有一个卒。该卒只能向下或者向右走，且卒采取的策略是先向下，下边走到头就向右，请问从（1,1）点走到（n,m）点可以怎样走，输出这些走法。

输入

两个整数n，m代表棋盘大小（3≤n≤8,3≤m≤8）

输出

卒的行走路线

样例

输入

3 3

输出

1:1,1->2,1->3,1->3,2->3,3
2:1,1->2,1->2,2->3,2->3,3
3:1,1->2,1->2,2->2,3->3,3
4:1,1->1,2->2,2->3,2->3,3
5:1,1->1,2->2,2->2,3->3,3
6:1,1->1,2->1,3->2,3->3,3

//解法一：参照迷宫的第一条路，深搜出迷宫的所有路径#include <bits/stdc++.h>
using namespace std;
//只能向下或者向右走：优先向下，其次向右 
int n,m;
int r[20][3];//存储行走路径 
//方向的变化 
int fx[3] = {0,1,0};
int fy[3] = {0,0,1}; 
int c;//计数器 void print(int k){c++;cout<<c<<":";//除了最后一个点以外 for(int i = 1;i < k;i++){cout<<r[i][1]<<","<<r[i][2]<<"->";}cout<<n<<","<<m<<endl;
} //向r数组下标为k的那一行，记录x,y点 
void dfs(int x,int y,int k){//记录坐标 r[k][1] = x;r[k][2] = y;//如果走到了终点，打印路径if(x == n && y == m){print(k);//停止递归函数，到了终点打印，就不需要继续递归了return; } int tx,ty;for(int i = 1;i <= 2;i++){tx = x + fx[i];ty = y + fy[i];//判断tx,ty有效if(tx>=1&&tx<=n&&ty>=1&&ty<=m){dfs(tx,ty,k+1);} }
} int main(){cin>>n>>m; //向r数组下标为1的那一行，记录1,1点 dfs(1,1,1);
}

//解法一：参照迷宫的第一条路，深搜出迷宫的所有路径#include <bits/stdc++.h>
using namespace std;
//只能向下或者向右走：优先向下，其次向右 
int n,m;
int r[20][3];//存储行走路径 
//方向的变化 
int fx[3] = {0,1,0};
int fy[3] = {0,0,1}; 
int c;//计数器 void print(int k){c++;cout<<c<<":";//除了最后一个点以外 for(int i = 1;i < k;i++){cout<<r[i][1]<<","<<r[i][2]<<"->";}cout<<n<<","<<m<<endl;
} //向r数组下标为k的那一行，记录x,y点 
void dfs(int x,int y,int k){//记录坐标 r[k][1] = x;r[k][2] = y;//如果走到了终点，打印路径if(x == n && y == m){print(k);//停止递归函数，到了终点打印，就不需要继续递归了return; } int tx,ty;for(int i = 1;i <= 2;i++){tx = x + fx[i];ty = y + fy[i];//判断tx,ty有效if(tx>=1&&tx<=n&&ty>=1&&ty<=m){dfs(tx,ty,k+1);} }
} int main(){cin>>n>>m; //向r数组下标为1的那一行，记录1,1点 dfs(1,1,1);
}

来源

深搜 递归