使用simulink仿真连续(离散)线性定长系统全维渐进状态观测器

本文主要是介绍使用simulink仿真连续(离散)线性定长系统全维渐进状态观测器，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

系统模型：

闭环极点设计分离性

设计系统输出反馈系数K

转换标准能控型

设计反馈矩阵G

仿真

matlab代码

simulink模型

仿真结果

仿真程序下载地址：连续定常系统全维状态观测器simulink仿真m代码-智慧城市文档类资源-CSDN下载

全维数字观测器输出反馈-智能家居文档类资源-CSDN下载

系统模型：

$\begin{gathered} A=\left[\begin{array}{cccc} 0 & -1 & 0 & 0 \\ 0 & 0 & 2 & 3 \\ 0 & 0 & 0 & -1 \\ 0 & 0 & 0 & 0 \end{array}\right], B=\left[\begin{array}{l} 0 \\ 0 \\ 0 \\ 1 \end{array}\right], C=\left[\begin{array}{llll} 1 & 0 & 0 & 0 \end{array}\right] \\ \dot{x}=A x+B u \\ y=C x \end{gathered}$

闭环极点设计分离性

闭环系统的极点包括 $\Sigma_{0}$ 直接状态反馈系统 $\Sigma_{K}=(A+KB,B,C)$ 的极点和观测器
$\Sigma_G$ 的极点两部分。但二者独立，相互分离。表明，由观测器构成状态反馈的闭环系统，其特征多项式等于矩阵（A+BK）与矩阵（A-GC）的特征多项式的乘积。亦即闭环系统的极点等于直接状态反馈（A+BK）的极点和状态观测器（A-GC）的极点之总和，而且二者相互独立。因此只要系统（A，B，C）能控能观，则系统的状态反馈矩阵K和观测器反馈矩阵G可分别进行设计。这个性质称为闭环极点设计的分离性。

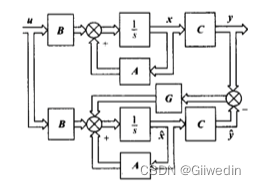
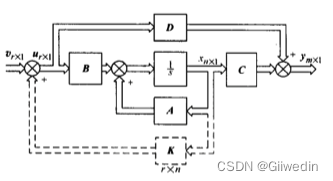
图1 渐进状态观测器图2输出反馈

$\hat{\hat{x}}=(A-G C) \hat{x}+G y+B u$ $\begin{aligned} &\dot{x}=(A+B K) x+B v \\ &y=(C+D K) x+D v \end{aligned}$

设计系统输出反馈系数K

证明系统能控性

$rank(\left[B A B A^{2} B A^{3} B\right])=4$

转换标准能控型

系统传递函数

$W(s)=C(s I-A)=\frac{-3 s+2}{s^{2}}$

线性非奇异变换矩阵

$T=\left[A^{3} B A^{2} B \quad A B \quad B\right]\left[\begin{array}{cccc} 1 & 0 & 0 & 0 \\ a 3 & 1 & 0 & 0 \\ a 2 & a 3 & 1 & 0 \\ a 1 & a 2 & a 3 & 1 \end{array}\right]$

标准能控1型

$\begin{aligned} &\tilde{A}=T^{-1} A T=\left[\begin{array}{llll} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{array}\right]\\ &\tilde{B}=T^{-1} B=\left[\begin{array}{l} 0 \\ 0 \\ 0 \\ 1 \end{array}\right]\\ &\tilde{C}=C T=\left[\begin{array}{llll} 2 & -3 & 0 & 0 \end{array}\right] \end{aligned}$

加入状态反馈增益矩阵

$\begin{aligned} \widetilde{K}=K T &=[k 0, k 1, k 2, k 3] \\ \tilde{A}+\tilde{B} \widetilde{K} &=\left[\begin{array}{cccc} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ k 0 & k 1 & k 2 & k 3 \end{array}\right] \end{aligned}$

闭环特征多项式

$f(\lambda)=|\lambda I-(\tilde{A}+\tilde{B} \widetilde{K})|=\lambda^{4}-k 3 \lambda^{3}-k 2 \lambda^{2}-k 1 \lambda-k 0$

使闭环极点与期望的极点相符求出增益K

$\begin{gathered} \lambda_{1,2}^{*}=-1, \lambda^{*}{ }_{3,4}=\pm j \\ f^{*}(\lambda)=(\lambda+1)^{2}\left(\lambda^{2}+1\right)=\lambda^{4}+2 \lambda^{3}+2 \lambda^{2}+2 \lambda+1 \\ f(\lambda)=f^{*}(\lambda) \\ \widetilde{K}=K T=[-1,-2,-2,-2] \\ K=[-0.5,1.75,7.25,-2] \end{gathered}$

设计反馈矩阵G

验证系统能观

$\operatorname{rank}\left[\begin{array}{c} C \\ C A \\ C A^{2} \\ C A^{3} \end{array}\right]=4$

观测器方程

$\begin{gathered} \left\{\begin{array}{c} \dot{\hat{x}}=A \hat{x}+B u+G(y-\hat{y}) \\ \hat{y}=C\hat{x} \end{array}\right. \\\left\{\begin{array}{c} \hat{x}=(A-G C) \hat{x}+B u+G y \\ \hat{y}=C \hat{x} \end{array}\right. \end{gathered}$

非奇异变换

$T^{-1}=\left[\begin{array}{llll} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{array}\right]\left[\begin{array}{c} C A^{3} \\ C A^{2} \\ C A \\ C \end{array}\right]$

能观标准2型

$\begin{aligned} &A=T^{-1} A T=\left[\begin{array}{llll} 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array}\right]\\ &\bar{B}=T^{-1} B=\left[\begin{array}{c} 2 \\ -3 \\ 0 \\ 0 \end{array}\right]\\ &\bar{C}=C T=\left[\begin{array}{llll} 0 & 0 & 0 & 1 \end{array}\right] \end{aligned}$

闭环特征多项式

$\begin{gathered} \bar{G}=T G=[g 0, g 1, g 2, g 3] \\ \ddot{A}-\tilde{G} C=\left[\begin{array}{llll} 0 & 0 & 0 & -g 0 \\ 1 & 0 & 0 & -g 1 \\ 0 & 1 & 0 & -g 2 \\ 0 & 0 & 1 & -g 3 \end{array}\right] \end{gathered}$

$f(\lambda)=|\lambda I-(\bar{A}-\bar{G} \bar{C})|=\lambda^{4}+g 3 \lambda^{3}+g 2 \lambda^{2}+g 1 \lambda+g 0$

使闭环极点与期望的极点相符求出增益G

$\begin{gathered} f^{*}(\lambda)=(\lambda+1)^{4}=\lambda^{4}+4 \lambda^{3}+6 \lambda^{2}+4 \lambda+1 \\ f(\lambda)=f^{*}(\lambda) \\ G=T G=[4,6,4,1] \\ G=[4,-6,-2.75,-0.5] \end{gathered}$

仿真

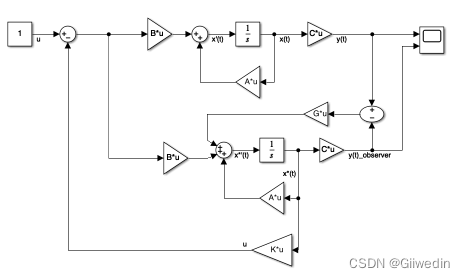
matlab代码

clear
A = [0 -1 0 0;0 0 2 3;0 0 0 -1;0 0 0 0];
B = [0;0;0;1];
C = [1 0 0 0];
%配置目标极点
K = acker(A,B,[-1,-1,-1+i,-1-i]);
%设计观测器
G=acker(A',C',[-1,-1,-1,-1])';

simulink模型

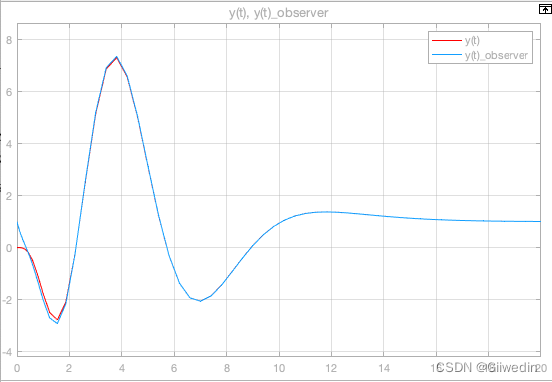
仿真结果

仿真程序下载地址：连续定常系统全维状态观测器simulink仿真m代码-智慧城市文档类资源-CSDN下载

全维数字观测器输出反馈-智能家居文档类资源-CSDN下载

使用simulink仿真连续(离散)线性定长系统全维渐进状态观测器_Giiwedin的博客-CSDN博客

使用drem对控制系统进行参数估计simulink仿真_Giiwedin的博客-CSDN博客

对给定干扰信号的simulink数字控制系统仿真_Giiwedin的博客-CSDN博客_simulink扰动信号

二相混合式步进电机闭环矢量控制simulink仿真（含仿真文件）_Giiwedin的博客-CSDN博客_步进电机数学模型

二相混合式步进电机开环细分控制simulink建模仿真含模型文件_Giiwedin的博客-CSDN博客

这篇关于使用simulink仿真连续(离散)线性定长系统全维渐进状态观测器的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

使用simulink仿真连续(离散)线性定长系统全维渐进状态观测器

系统模型：

闭环极点设计分离性