数学笔记——直角坐标方程转参数方程

本文主要是介绍数学笔记——直角坐标方程转参数方程，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

背景

学习matlab三维作图时遇到的一道题，搞不懂为什么要将直角方程转换成参数方程，在经过多次直角作图失败后，还是决定老老实实学下怎么将直角方程转参数方程，然后使用参数方程进行三维作图。

原式：$x^2+(y-5{)}^2=16$

需求：将求得原式绕x轴旋转一周所形成的旋转曲面方程。

思路：将原式转换成参数方程，再进行旋转操作。

第一步，原式转换成参数方程

给定圆的方程$x^2+(y-5{)}^2=16$，我们可以将其转化为极坐标形式：
$x=rcos\theta$
$y-5=rsin\theta$
其中，$r$为极径，$\theta$为极角。

将$y-5=rsin\theta$代入$x^2+(y-5{)}^2=16$中，得到：
$x^2+(rsin\theta {)}^2=16$

化简后得到：
$x^2+r^{2}si{n}^2\theta =16$

再将$x=rcos\theta$代入，得到：
$(rcos\theta {)}^2+r^{2}si{n}^2\theta =16$

化简后得到：
$r^2(co{s}^2\theta +si{n}^2\theta )=16$

由于$co{s}^2\theta +si{n}^2\theta =1$，
所以：$r^2=16$
解得$r=4$。
因此，圆的极径$r$为4。

将$r=4$代入$x=rcos\theta$和$y-5=rsin\theta$中，得到圆的参数方程：
$x=4cos\theta$
$y=5+4sin\theta$
$z=0$

这样，我们就得到了圆的参数方程。通过调整$\theta$的取值，可以得到圆上的不同点的坐标。

第二步，将参数方程绕x轴旋转一周

如果将该圆曲面绕x轴旋转一周，可以得到一个旋转体，即一个圆柱体。
对于圆的参数方程$x=4cos\theta ，y=5+4sin\theta ，z=0$，我们将z坐标保持不变，即$z=0$。然后，将$x$和$y$坐标分别替换为$x^{\prime }$和$y^{\prime }$，表示旋转后的坐标。
对于旋转体的参数方程，我们可以使用极坐标的旋转公式来推导。
$x^{\prime }=x$
$y^{\prime }=ycos\phi -zsin\phi$
$z^{\prime }=ysin\phi +zcos\phi$
其中，$\phi$为旋转角度。

对于绕x轴旋转一周，我们可以令$\phi =\theta$，即旋转角度等于极角。
将$x=4cos\theta ，y=5+4sin\theta ，z=0$代入旋转公式，得到：
$x^{\prime }=4cos\theta$
$y^{\prime }=(5+4sin\theta )cos\theta$
$z^{\prime }=(5+4sin\theta )sin\theta$

这样，我们就得到了旋转体（圆柱体）的参数方程：
$x^{\prime }=4cos\theta$
$y^{\prime }=(5+4sin\theta )cos\theta$
$z^{\prime }=(5+4sin\theta )sin\theta$

这个参数方程描述了绕x轴旋转一周后的曲面的形状。

结果程序与图形

alpha = [0:0.1:2*pi]‘;beta = 0:0.1:2*pi;
x = 4*cos(alpha)*ones(size(beta));
y = (5 + 4*sin(alpha))*cos(beta);
z = (5 + 4*sin(alpha)) * sin(beta);
surf(x,y,z)

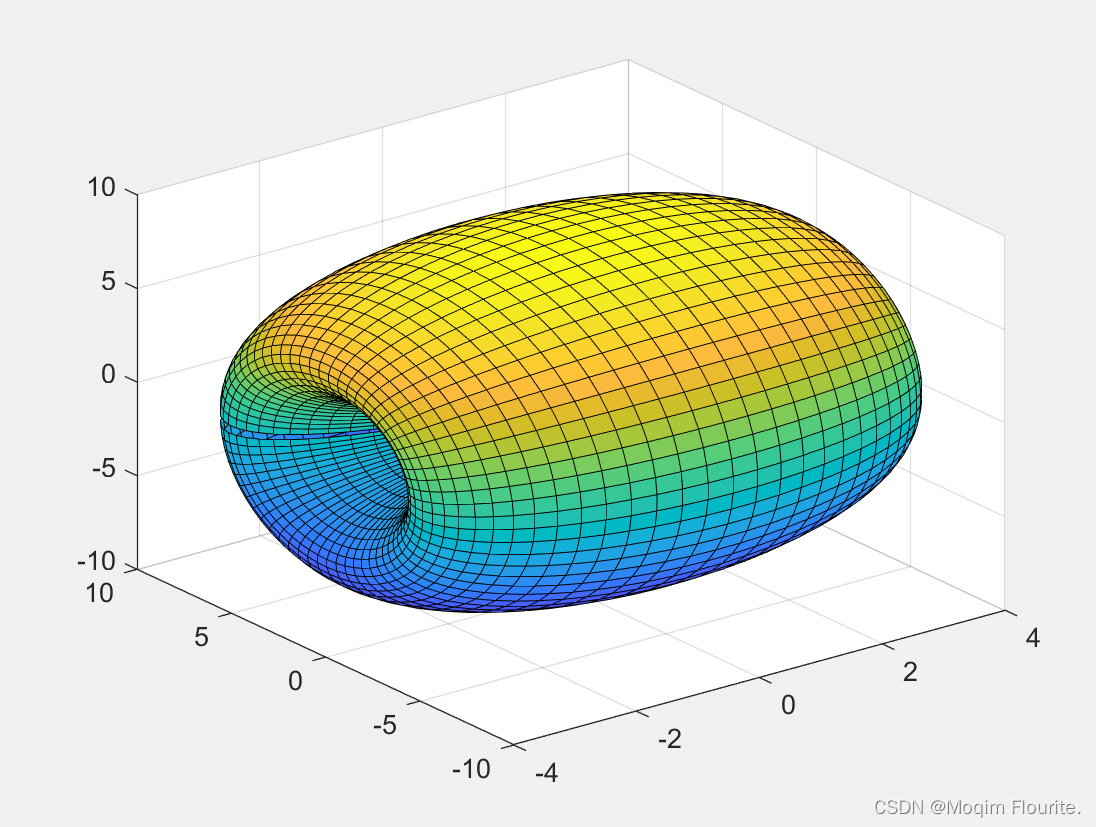
注

计算内容主要还是套各种公式，以前的知识点还是需要补一下的。

以上过程均来自AI，此内容仅作本人学习记录使用。

这篇关于数学笔记——直角坐标方程转参数方程的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---