Leha and security system（Codeforces 794F）（线段树懒标记）

题目

CF

$a_i\le 10^9$

思路

不难想到用线段树维护， $sum[i][j]$ 表示区间 $[l,r]$ 中数码为 $j$ 的和除以 $j$
但是如何维护呢，我们记 $lazy[i][j]$ 表示 $[l,r]$ 中数码为 $j$ 的和转移到数码为 $lazy[i][j]$ 的和，即时生效（即对儿子的起作用）

void PushDown(int i){for(int t=0;t<=9;t++)tmp[t]=sum[lch][t];for(int t=0;t<=9;t++)lazy[lch][t]=lazy[i][lazy[lch][t]];for(int t=0;t<=9;t++)if(lazy[i][t]!=t){tmp[lazy[i][t]]+=sum[lch][t];tmp[t]-=sum[lch][t];}for(int t=0;t<=9;t++)sum[lch][t]=tmp[t];for(int t=0;t<=9;t++)tmp[t]=sum[rch][t];for(int t=0;t<=9;t++)lazy[rch][t]=lazy[i][lazy[rch][t]];for(int t=0;t<=9;t++)if(lazy[i][t]!=t){tmp[lazy[i][t]]+=sum[rch][t];tmp[t]-=sum[rch][t];}for(int t=0;t<=9;t++)sum[rch][t]=tmp[t];for(int t=0;t<=9;t++)lazy[i][t]=t;return ;
}

$PushDown$ 写得非常玄幻,我们可以一步步看

for(int t=0;t<=9;t++)lazy[lch][t]=lazy[i][lazy[lch][t]];

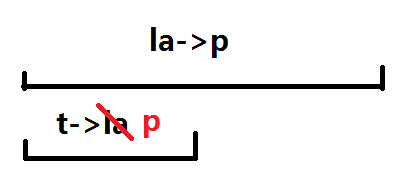
想一想， $lazy$ 是对儿子生效的，也就是说本层的 $lazy$ 是不会影响自己的，我们可以先将儿子的 $lazy$ 修改，本来是孙子要从 $t->la$ 但是又来了一个 $la->p$ 于是就变为了 $t->p$

for(int t=0;t<=9;t++)tmp[t]=sum[lch][t];
for(int t=0;t<=9;t++)if(lazy[i][t]!=t){tmp[lazy[i][t]]+=sum[lch][t];tmp[t]-=sum[lch][t];}
for(int t=0;t<=9;t++)sum[lch][t]=tmp[t];

现在和儿子的 $lazy$ 没有任何关系了，我们就只更改儿子的 $sum$

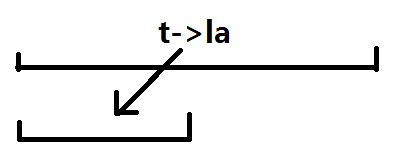
但是我们不能直接修改儿子的 $sum$ 因为我们需要这个历史版本去更新这个儿子其他的 $sum$ 于是就用了一个临时数组

注意你修改后不能直接将 $tmp$ 赋值为0(第6行)，因为可能已经保存了一些修改后 $sum$ 的信息
然后就常规了

代码

//#pragma GCC optimize(2)
#include<set>
#include<map>
#include<stack>
#include<cmath>
#include<queue>
#include<cstdio>
#include<vector>
#include<climits>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define LL long long
using namespace std;
int read(){bool f=0;int x=0;char c=getchar();while(c<'0'||'9'<c){if(c=='-')f=1;c=getchar();}while('0'<=c&&c<='9') x=(x<<3)+(x<<1)+(c^48),c=getchar();return !f?x:-x;
}
#define lch (i<<1)
#define rch (i<<1|1)
#define MAXN 200000
#define INF 0x3f3f3f3f
int lazy[5*MAXN+5][10];
LL sum[5*MAXN+5][10];
void PushUp(int i){for(int t=0;t<=9;t++)sum[i][t]=sum[lch][t]+sum[rch][t];return ;
}
LL tmp[10];
void PushDown(int i){for(int t=0;t<=9;t++)tmp[t]=sum[lch][t];for(int t=0;t<=9;t++)lazy[lch][t]=lazy[i][lazy[lch][t]];for(int t=0;t<=9;t++)if(lazy[i][t]!=t){tmp[lazy[i][t]]+=sum[lch][t];tmp[t]-=sum[lch][t];}for(int t=0;t<=9;t++)sum[lch][t]=tmp[t];for(int t=0;t<=9;t++)tmp[t]=sum[rch][t];for(int t=0;t<=9;t++)lazy[rch][t]=lazy[i][lazy[rch][t]];for(int t=0;t<=9;t++)if(lazy[i][t]!=t){tmp[lazy[i][t]]+=sum[rch][t];tmp[t]-=sum[rch][t];}for(int t=0;t<=9;t++)sum[rch][t]=tmp[t];for(int t=0;t<=9;t++)lazy[i][t]=t;return ;
}
void Build(int i,int L,int R){for(int t=0;t<=9;t++)lazy[i][t]=t,sum[i][t]=0;if(L==R){int x=read(),tmp=1;while(x)sum[i][x%10]+=tmp,tmp*=10,x/=10;return ;}int Mid=(L+R)>>1;Build(lch,L,Mid),Build(rch,Mid+1,R);PushUp(i);return ;
}
void Modify(int i,int L,int R,int qL,int qR,int x,int y){if(qL<=L&&R<=qR){for(int t=0;t<=9;t++)if(lazy[i][t]==x){lazy[i][t]=y;sum[i][y]+=sum[i][x];sum[i][x]=0;}return ;}PushDown(i);int Mid=(L+R)>>1;if(qL<=Mid)Modify(lch,L,Mid,qL,qR,x,y);if(Mid+1<=qR)Modify(rch,Mid+1,R,qL,qR,x,y);PushUp(i);return ;
}
LL Query(int i,int L,int R,int qL,int qR){if(qL<=L&&R<=qR){LL ret=0;for(int t=0;t<=9;t++)ret+=sum[i][t]*t;return ret;}PushDown(i);LL ret=0;int Mid=(L+R)>>1;if(qL<=Mid)ret+=Query(lch,L,Mid,qL,qR);if(Mid+1<=qR)ret+=Query(rch,Mid+1,R,qL,qR);return ret;
}
int main(){int n=read(),q=read();Build(1,1,n);for(int i=1;i<=q;i++){int opt=read();if(opt==1){int l=read(),r=read(),x=read(),y=read();if(x==y) continue;Modify(1,1,n,l,r,x,y);}else{int l=read(),r=read();printf("%lld\n",Query(1,1,n,l,r));}}return 0;
}

思考

分清即时生效和非即时生效的 $lazy$ ，即时生效的 $PushDown$ 比较难写时可以将修改儿子 $lazy$ 和其它信息分开处理，记住即时生效写法儿子的 $lazy$ 一定不会影响儿子本身，写 $PushDown$ 一定要思路清晰。