本文主要是介绍深度学习课程总结(stage1),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、线性分类与感知机
线性回归
(1)定义:利用数理统计中回归分析,来确定两种或两种以上变量间相
互依赖的定量关系的一种统计分析方法。
(2)要素:训练集(即输入数据),比如预测房价和面积的关系时,面积就是训练集
输出数据,模型(映射关系),条目数
(3)多维问题:
假设原问题和n个因素有关,则可以构造代价函数:
其中前者是真实值,后者是预测值,我们的目标是使损失函数最小
线性二分类问题
(1)定义:线性分类器则透过特征的线性组合来做出分类决定,以达到
此种目的。简言之,样本通过直线(或超平面)可分
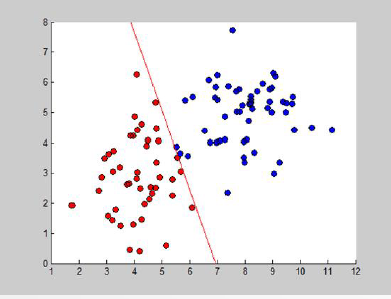
(2)输入是特征向量,输出有多种可能,如果是二分类问题,则是0和1,如果输出是某类的概率,则是0到1之间的数字
(3)为了最终获得0到1之间的概率,我们构造了sigmoid函数:
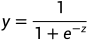
其中,z是特征x的线性组合
因此,可以构造如下的损失函数:
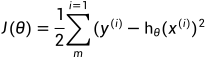
其中,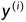 是gt,只能取0或者1,而
是gt,只能取0或者1,而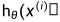 是通过sigmoid函数获得的,这种回归叫做softmax
是通过sigmoid函数获得的,这种回归叫做softmax
(4)求解对应J最小时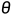 的大小的方法
的大小的方法
可以认为J是通过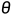 的一个差分的方式构成的,因此我们可以采用以下方法:
的一个差分的方式构成的,因此我们可以采用以下方法:
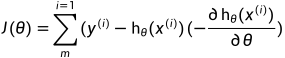
而由sigmoid函数的性质,可知:
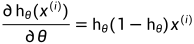
对数回归和多分类回归
二分类问题的交叉熵
由于二分类问题的输出只有0和1,因此可以将损失函数写作:
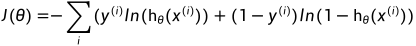
对其最小化,可得: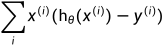
感知机模型
(1)由输入到输出的模型如下:
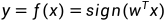

为损失函数,我们的目标是使损失函数最小
二、多层前馈网络与误差反传算法
多层感知机:
(1)用处:解决线性不可分问题
(2)结构:在输入和输出之间加入隐藏层
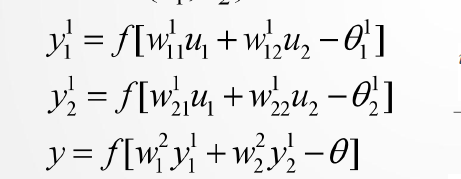
(3)定理:① 若隐层节点(单元)可任意设置,用三层阈值节点的
网络,可以实现任意的二值逻辑函数。
② 若隐层节点(单元)可任意设置,用三层S型非线性特
性节点的网络,可以一致逼近紧集上的连续函数或按 范数逼近紧
集上的平方可积函数。
多层前馈网络以及BP算法:
(1)组成:
① 网络结构:一般称为BP神经网络
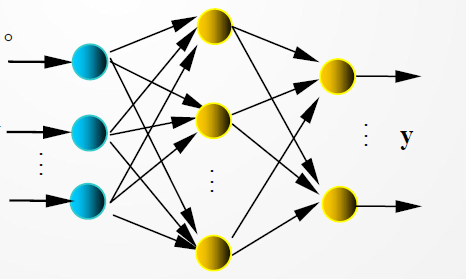
② 正向传播:输入信号从输入层经隐层,传向输出层,若输出层得到了期望的输出,则学习算法结束;否则,转至反向传播
③ 反向传播:是将误差(样本输出与网络输出之差)按原联接通路反向计算,由梯度下降法调整各层节点的权值和阈值,使误差减小。
(2)算法流程(来源于本人的另一篇博客,链接:https://blog.csdn.net/aliezaliezaliez/article/details/126540495?spm=1001.2014.3001.5502)
以一维度的w和b为例,
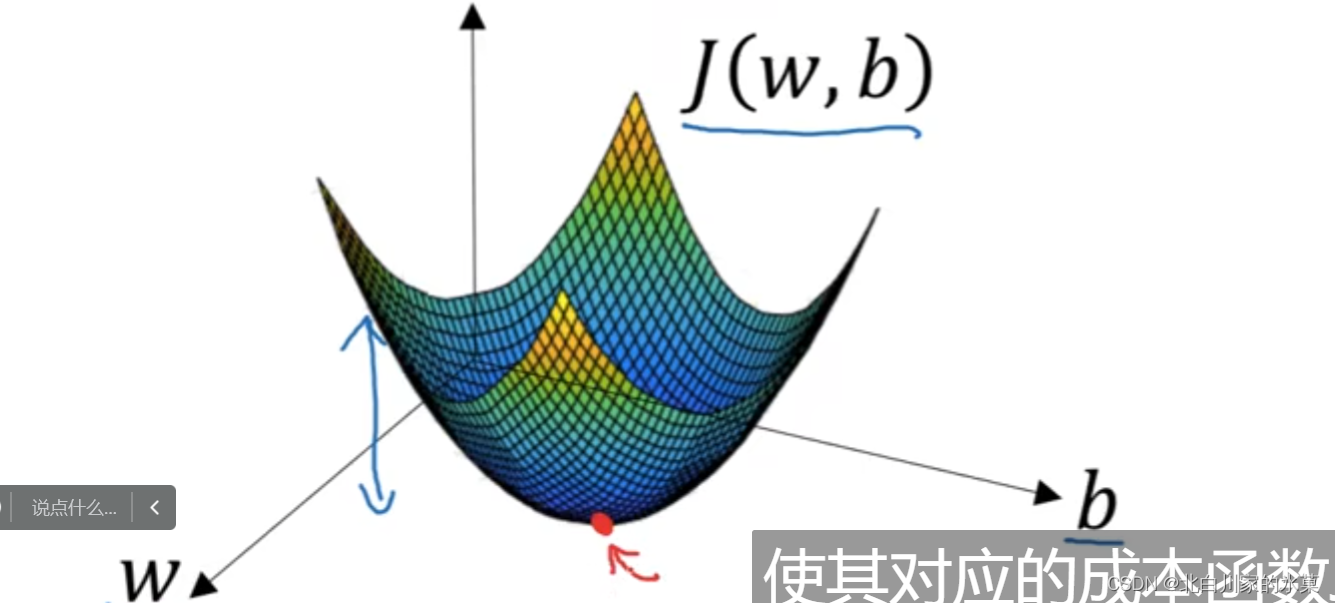
我们希望从起始点沿着梯度最大的路径以一定的步长向下降,直到达到最优解,或者接近最优解
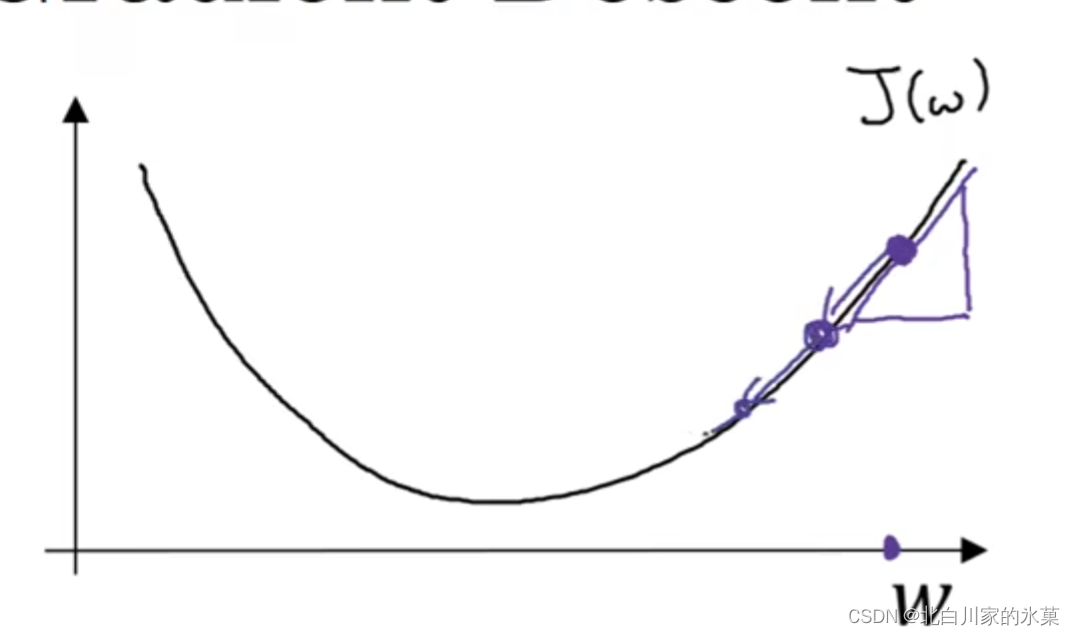
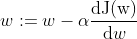
在代码中,经常把
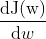
写作
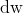
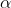
成为学习率,决定了每次下降的步长
对于J(w,b)同理
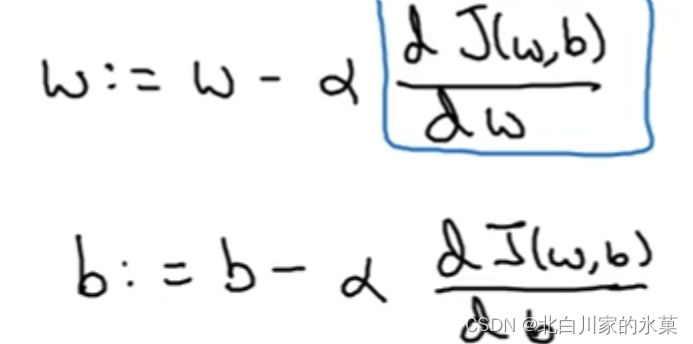

编辑
即分别沿着两个变量的最大梯度下降
数学基础 ————导数
① 计算图
例:
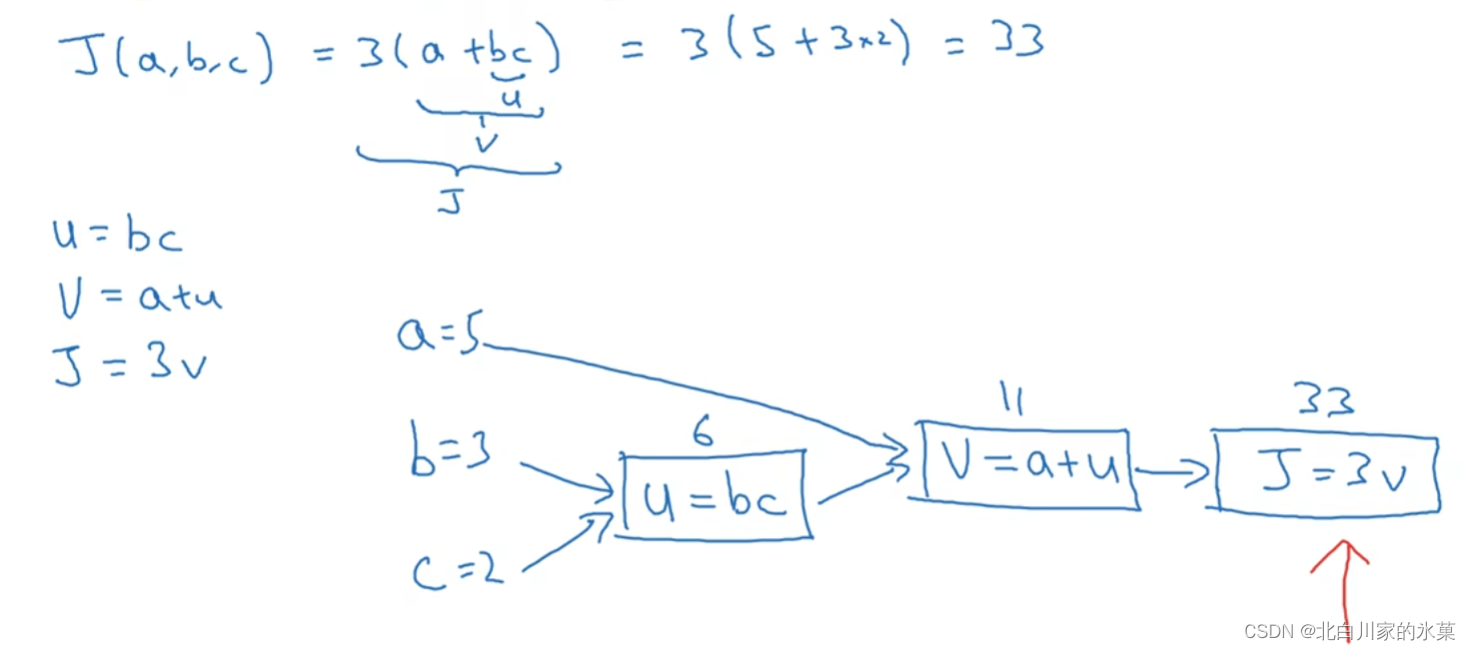

编辑
该过程的逆过程,就是导数的求取过程


编辑
说完数学基础后,可以进一步研究logistics 中的梯度下降
下面这个图万分的重要!!!!!!!!!!!
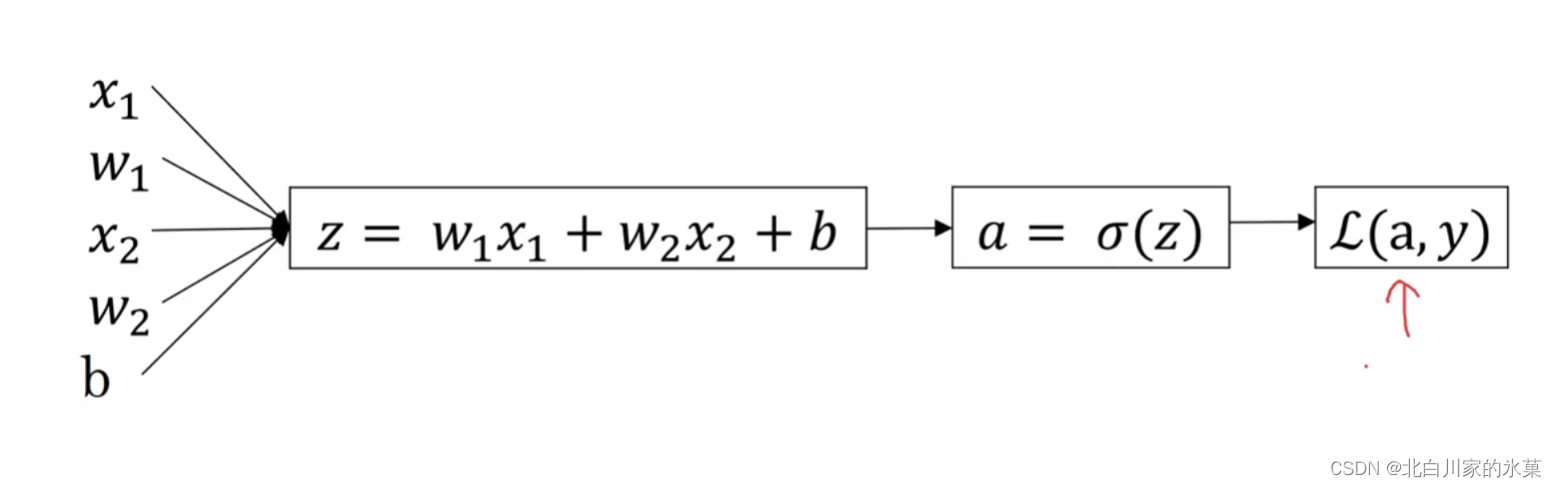
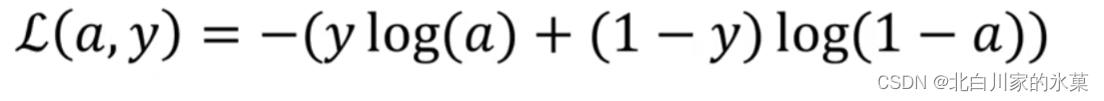
则:
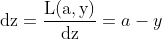
当输入有m个样本时:


编辑
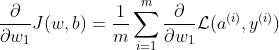
代码实现思路如下:

这里面
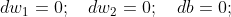

编辑不加带i的角标,因为他们是求和的形式
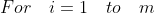
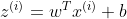
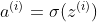
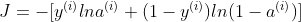

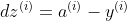

编辑(这个前面用链式法则推过)
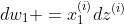

(这个右侧本质上加的就是某个输入的
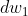
,对J求导即可,那也就是用链式法则推导,其实就是对z先求导,然后z对w求导所以出来了
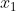
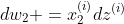
...
这里
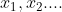
这些,代表的是特征的个数,例如图片识别时,每一个图片分为r,g,b三原色,每一种原色都有64×64的像素,因此在这里,
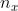

编辑的个数为3×64×64个
如果这里x的维度n比较大,可能也需要写一个循环
对于m,是输入的个数,以图片识别为例,就是图片的张数
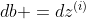
(z对b求偏导数是1)
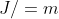

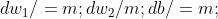

编辑(前文公式可以看出来)
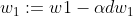
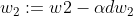

编辑
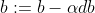

编辑
(梯度下降法)
使用for循环会使代码变得低效,因此我们可以用向量化来代替for循环
5.向量化
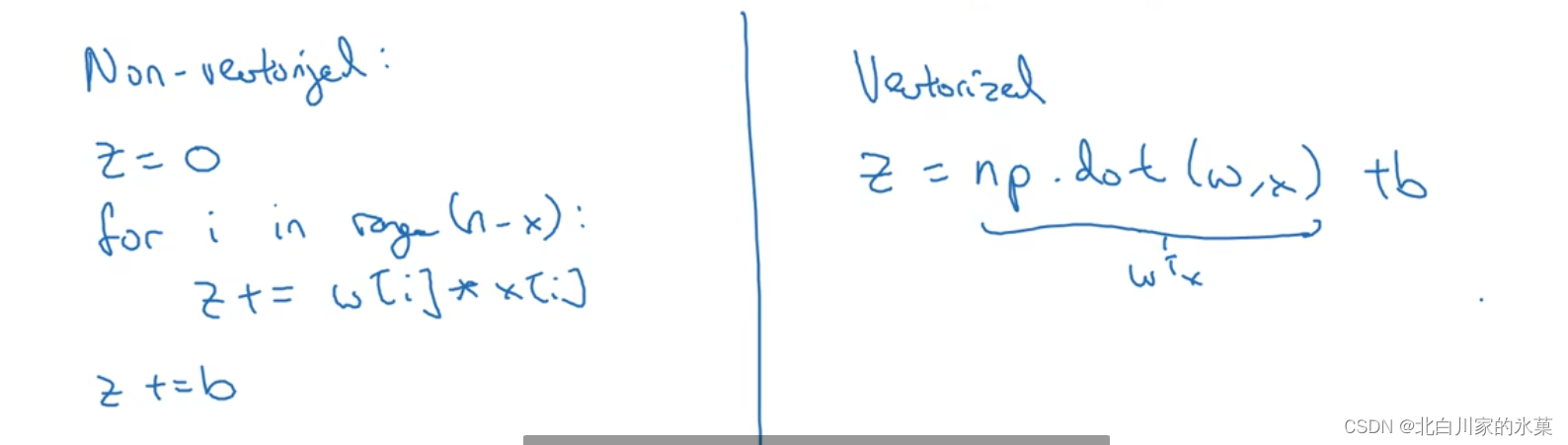

编辑
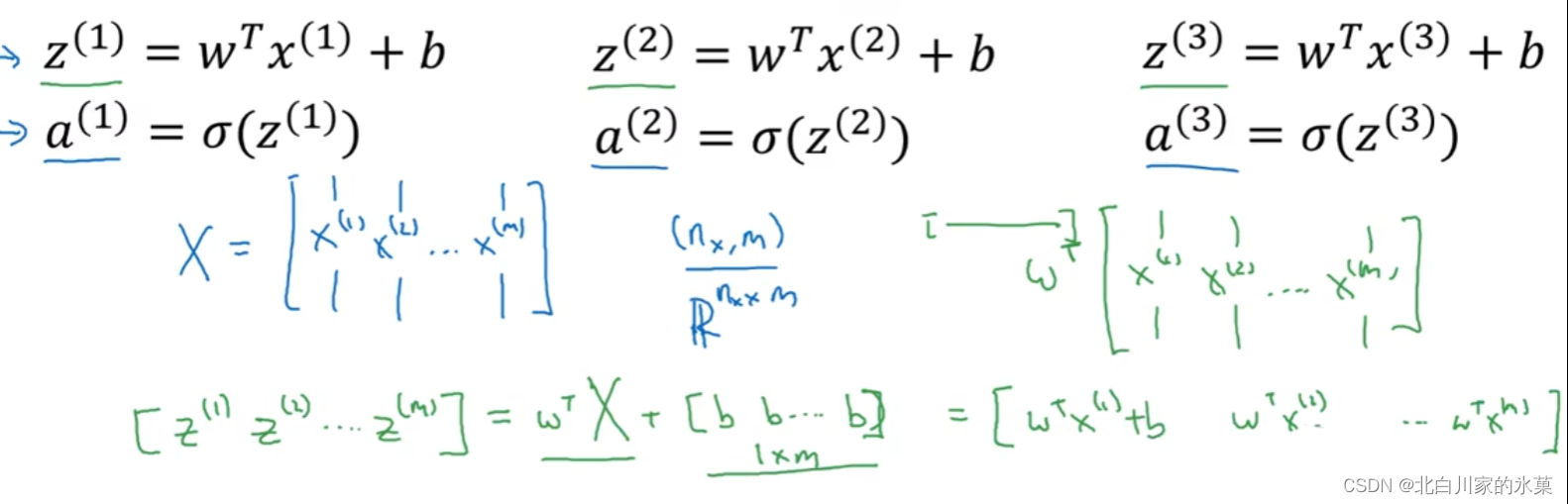
这篇关于深度学习课程总结(stage1)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





