c++中计算2得n次方_「专题」解析一元一次方程的知识点以及实际应用

解方程的内容大家基本从小学就开始学习，小学主要是求解，而中学阶段主要学习根据条件列方程并求解。因此，涉及一元一次方程的应用题，可以说是中学阶段学习方程问题的第一个难点。下面让我们先来解决初中可能遗留的第一个问题——一元一次方程。

什么是一元一次方程

我们将含有未知数的等式就叫做方程，那么什么是一元一次方程呢？只含有一个未知数(元)x，未知数x的指数都是1(次)，这样的方程叫做一元一次方程。

一元一次方程的标准形式：

ax+b=0(x是未知数，a、b是已知数，且a≠0)。

一元一次方程必须同时满足4个条件：

(1)它是等式;

(2)分母中不含有未知数;

(3)未知数最高次项为1;

(4)含未知数的项的系数不为0。

如何解一元一次方程

01

解方程的一般步骤

(1)去分母：方程两边同乘各分母的最小公倍数

(2)去括号：按去括号法则和分配律

(3)移项：把含有未知数的项移到方程一边，其他项都移到方程的另一边，移项要变号

(4)合并：把方程化成ax = b (a≠0)形式

(5)系数化为1：在方程两边都除以未知数的系数a，得到方程的解

02

方程的解：

使方程中等号左右两边相等的未知数的值，叫做方程的解。

注意：方程的解和解方程是不同的概念，方程的解实质上是求得的结果，它是一个数值(或几个数值)，而解方程的含义是指求出方程的解或判断方程无解的过程。

实际上，解一元一次方程就是在运用等式的性质进行求解。

● 等式的性质

(1)等式两边都加上(或减去)同个数(或式子)，等式仍然成立。

用式子形式表示为：如果a=b，那么a±c=b±c

(2)等式两边乘同一个数，或除以同一个不为0的数，等式仍然成立。

用式子形式表示为：如果a=b，那么ac=bc;如果a=b(c≠0)，那么a/c=b/c

(3)等式两边同时乘方(或开方)，等式仍然成立。

03

方程的解的检验方法：

首先把未知数的值分别代入方程的左、右两边计算它们的值，其次比较两边的值是否相等，从而得出结论。

对初学的同学来讲，解一元一次方程的方法很容易掌握，但类似于前面的有理数混合运算，每个题都感觉会做，但就是不能保证全对。

因此，在学习时，一方面要反复关注方程变形的法则依据，用法则指导变形步骤，另一方面还需不断关注易错点和追求计算过程的简捷。

如何利用一元一次方程解应用题

一元一次方程的应用题主要是从实际问题中寻找相等关系，分析实际问题中的已知量和未知量，找出相等关系，列出方程，使同学们逐步建立列方程解决实际问题的思想方法。基本步骤

01

基本步骤：

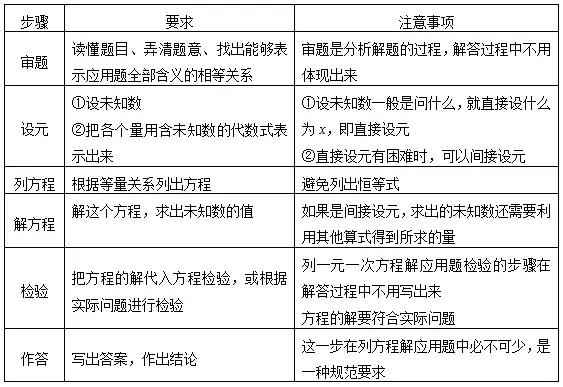
02

设未知数的方法:

(1)“直接设元”：题目里要求的未知量是什么，就把它设为未知数，多适用于要求的未知数只有一个的情况。

(2)“间接设元”：有些应用题，若直接设未知数很难列出方程，或者所列的方程比较复杂，可以选择间接设未知数，而解得的间接未知数对确定所求的量起中介作用。

(3)“辅助设元”：有些应用题不仅要直接设未知数，而且要增加辅助未知数，但这些辅助未知数本身并不需要求出，它们的作用只是为了帮助列方程，同时为了求出真正的未知量，可以在解题时消去。

(4)“部分设元”与“整体设元”转换：当整体设元有困难时，可以考虑设其一部分为未知数，反之亦然。

注意：

◆ 初中列方程解应用题时，怎么列简单就怎么列(即所列的每一个方程都直接的表示题意)，不用担心未知数过多，简化审题和列方程的步骤，把难度转移到解方程的步骤上。

◆ 设未知数时，要标明单位，在列方程时，如果题中数据的单位不统一，必须把单位换算成统一单位，尤其是行程问题里尤其需要注意这个问题。

应用题常见类型

学习中，部分同学很容易忽视对一元一次方程的联系，实际上该方程牵涉到许多的实际问题，而与实际问题的结合正是大部分同学的失分点。

工程问题：

当题目中未给出工作总量时，设工作总量为单位1，即完成某项任务的各工作量的和＝总工作量＝1。

工作总量=工作时间×工作效率

各部分工作量之和=1

行程问题

涉及行程问题，我们经常采用“画图分析法”，利用图形分析行程问题是数形结合思想在数学中的体现，依照题意画出有关图形，使图形各部分具有特定的含义，通过图形找相等关系是解决问题的关键，从而取得列方程的依据，最后利用量与量之间的关系(可把未知数看做已知量)，填入有关的代数式是获得方程的基础。

路程=速度×时间

相遇路程=速度和×相遇时间

追及路程=速度差×追及时间

顺流速度=静水速度+水流速度

逆流速度=静水速度－水流速度水流速度=×(顺流速度－逆流速度)

火车过桥问题是一种特殊的行程问题，需要注意从车头至桥起，到车尾离桥止，火车所行距离等于桥长加上车长，列车过桥问题的基本数量关系为：

车速×过桥时间=车长+桥长。

利润问题：

在现实生活中，购买商品和销售商品时，经常会遇到进价、标价、售价、打折等概念，我们必须了解这些概念的实际应用，比如：商品打几折出售，就是按原标价的百分之几十出售，商品打8折出售，即按原标价的80%出售。在了解这些基本概念的基础上，还必须掌握以下几个等量关系：

利润=售价－进价

利润=进价×利润率

实际售价=标价×打折率

调配问题：

调配与比例问题在日常生活中十分常见，比如：合理选取方案，安排工人生产，按比例选取工程材料，调剂人数或货物等。

调配问题中关键是要认识清楚部分量、总量以及两者之间的关系。在调配问题中主要考虑“总量不变”；而在比例问题中则主要考虑总量与部分量之间的关系，或是量与量之间的比例关系。

对于一元一次方程，从操作步骤上来讲，大部分同学都能够明晰，但是进行每个步骤是需要注意的细节问题，是思维瑕点，需要反复关注易错点，并落实理解记忆，才能提高方程的正确率。此外，针对，一元一次方程的应用题，必须要明晰各类题型之间涉及的关系公式，否则就是“求助无门”！

看完后不要忘记结合“每日一题”进行练习哟！