基于逐次凸近似(Successive Convex Approximation)的非凸二次规划问题求解---MATLAB程序

本文引用了上海财经大学崔雪婷老师最优化理论与方法课程，课程链接如下：

【最优化理论与方法-第十二讲-二次规划】 https://www.bilibili.com/video/BV1vQ4y1P77A/?p=4&share_source=copy_web&vd_source=ec4b99096a4967b6330aae8eaef5e99b

崔老师讲最优化讲的特别好！满分推荐！

逐次凸近似(Successive Convex Approximation, SCA)是一种优化算法，主要应用于求解非凸优化问题。它的基本思想是将一个非凸问题转化为包含多个凸子问题的序列，通过不断的求解凸子问题逼近原问题的最优解。

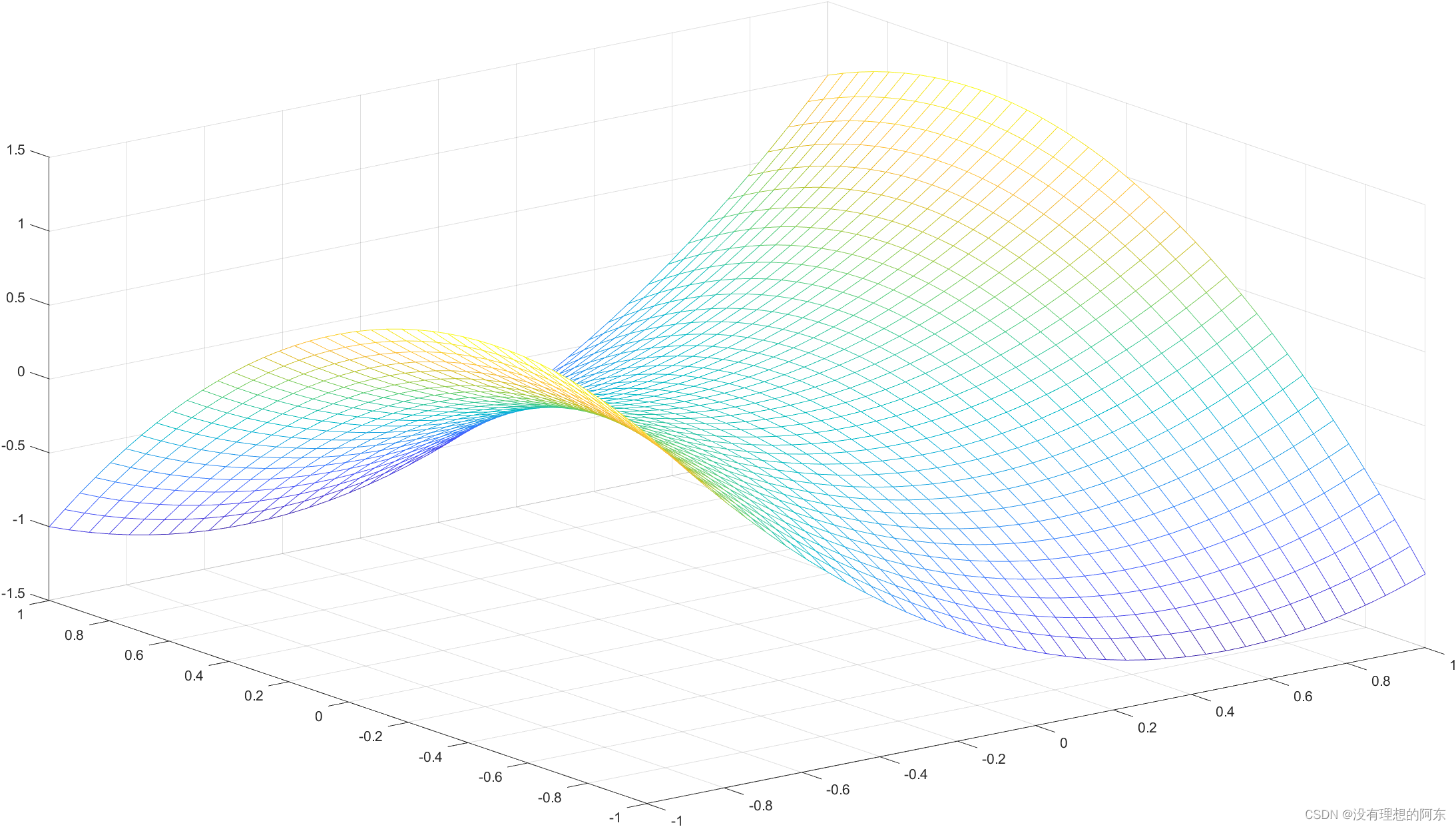
 图1 非凸函数

现考虑如下非凸二次规划问题，其函数图像如图1所示。

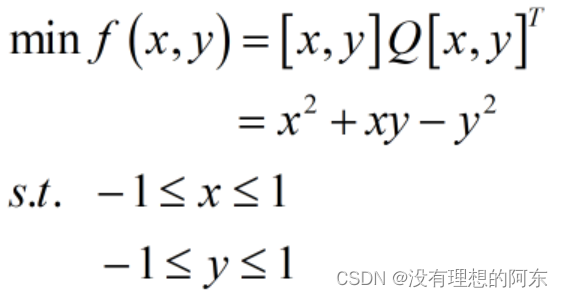
问题1

其中，

原问题的目标函数可以通过特征值分解转化为凸函数减去凸函数的形式，凸函数减去凸函数未必是凸函数。

[V,D] = eig(Q);%计算A的特征值对角阵D和特征向量V，使AV=VD成立

其中,矩阵P和N都是半正定矩阵，矩阵D的表达式如下所示：

其中，,。

原问题的目标函数可以转化为：

对目标函数的第二项在点处进行凸近似，即在点处进行一阶泰勒展开：

至此，原问题可转化为：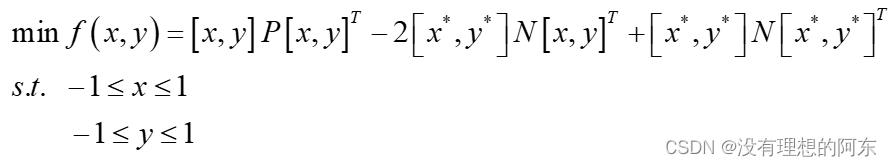

 问题2

这样一来，就可以将原来的非凸二次规划问题转化为凸二次规划问题进行求解。

定理：若是问题2的最优解，则必然是问题1的KKT点(在崔老师的视频中有证明)。

因此，只要找到一个点使得是问题二的最优解，即可求得原问题的近似最优解。(注意：SCA不能保证得到全局最优解，但解的质量较高)

读到这里，想必各位心中都会有一个疑问：点要这么确定呢？SCA算法就是为了找到这样一个点，算法步骤如下所示：

1）令，取(初值对结果的影响较大，建议取可行域中点)；

2）求解近似优化问题(即问题2)，得到子问题最优解;

3）若，输出；否则，令，转至2）。

MATLAB程序：

clear all
close all
clcQ=[1,0.5;0.5,-1];x=sdpvar(2,1);
xmin=-1;
xmax=1;
Constraints=[];
Constraints=[Constraints,xmin<=x<=xmax];
ops = sdpsettings('solver', 'gurobi', 'verbose', 0);[V,D] = eig(Q);%计算A的特征值对角阵D和特征向量V，使AV=VD成立
lambda_P=D;
lambda_N=-D;
lambda_P(find(D<0))=0;
lambda_N(find(D>0))=0;
P=V*lambda_P*V';
N=V*lambda_N*V';
x0=[0.5;0.5];
x_temp=x0;
while(1)f_k=(x'*P*x-2*x_temp'*N*x+x_temp'*N*x_temp);sol=solvesdp(Constraints,f_k,ops);display([sol.info,' 目标函数值：',num2str(value(x_temp'*Q*x_temp))])x_temp_before=x_temp;x_temp=value(x);if sqrt(sum((x_temp-x_temp_before).^2)/length(x_temp))<1e-10breakend
end
x_result=x_tempX = gridsamp([-1 -1;1 1], 40);
[m,~]=size(X);
YX=zeros(m,1);
for i=1:size(X,1)x=X(i,:);y=x*Q*x';YX(i)=y;
end
X1 = reshape(X(:,1),40,40); X2 = reshape(X(:,2),40,40);
YX = reshape(YX, size(X1));
figure(1), mesh(X1, X2, YX)%绘制预测表面
hold on
scatter3(x_temp(1),x_temp(2),x_temp'*Q*x_temp,200,'r','pentagram','filled')

结果展示：

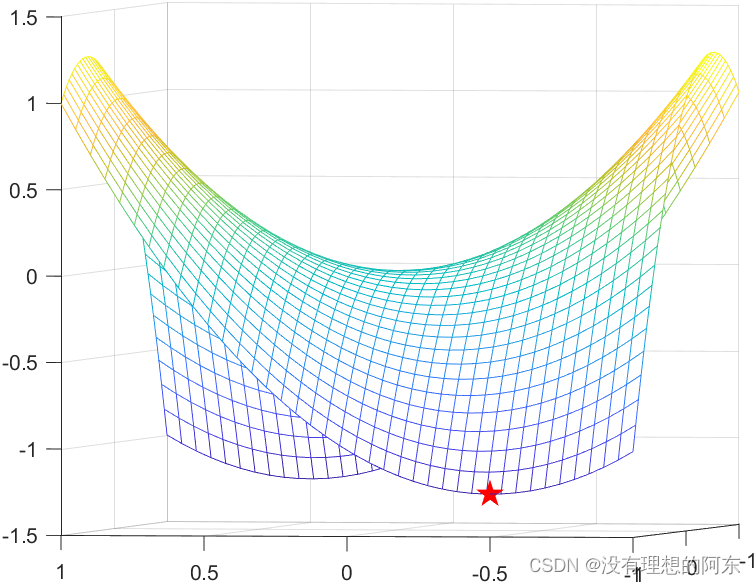
原问题：

clear all
close all
clcx=sdpvar(2,1);
xmin=-1;
xmax=1;
Constraints=[];
Constraints=[Constraints,xmin<=x<=xmax];
Q=[1,0.5;0.5,-1];
[V,D] = eig(Q);%计算A的特征值对角阵D和特征向量V，使AV=VD成立
lambda_P=D;
lambda_N=-D;
lambda_P(find(D<0))=0;
lambda_N(find(D>0))=0;
P=V*lambda_P*V';
N=V*lambda_N*V';
% P-N
f=x'*Q*x;%x(1)^2-x(2)^2+x(1)*x(2)
% x'*P*x-x'*N*x
ops = sdpsettings('solver', 'gurobi', 'verbose', 0);
sol=solvesdp(Constraints,f,ops);
x=value(x);
display([sol.info,' 目标函数值：',num2str(value(x'*Q*x))])

问题属性：对于非凸二次规划问题，gurobi会将原问题转化为MIP问题进行求解，如图2所示。本文举的例子比较简单，gurobi可以在短时间内求解成功，但对于大规模的非凸二次规划问题，使用gurobi进行求解会面临NP-Hard问题，计算负担较大，用SCA算法可以大大缩短计算时间。

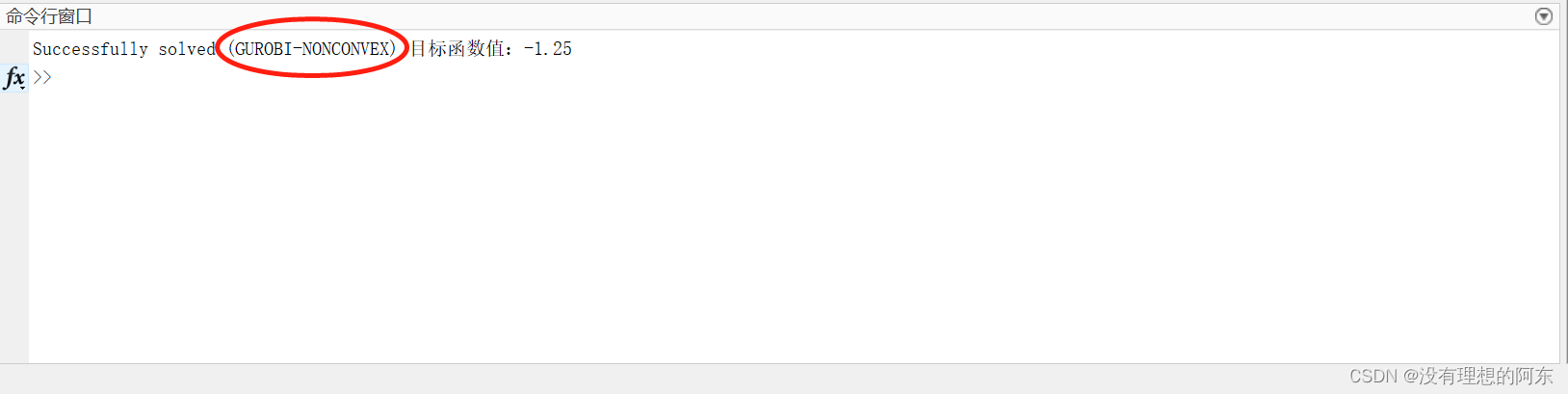
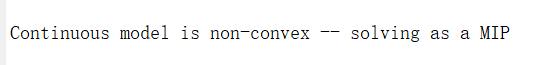
图2

其他子函数：

function  S = gridsamp(range, q)
%GRIDSAMP  n-dimensional grid over given range
%
% Call:    S = gridsamp(range, q)
%
% range :  2*n matrix with lower and upper limits
% q     :  n-vector, q(j) is the number of points
%          in the j'th direction.
%          If q is a scalar, then all q(j) = q
% S     :  m*n array with points, m = prod(q)% hbn@imm.dtu.dk  
% Last update June 25, 2002[mr n] = size(range);    dr = diff(range);
if  mr ~= 2 | any(dr < 0)error('range must be an array with two rows and range(1,:) <= range(2,:)')
end 
sq = size(q);
if  min(sq) > 1 | any(q <= 0)error('q must be a vector with non-negative elements')
end
p = length(q);   
if  p == 1,  q = repmat(q,1,n); 
elseif  p ~= nerror(sprintf('length of q must be either 1 or %d',n))
end % Check for degenerate intervals
i = find(dr == 0);
if  ~isempty(i),  q(i) = 0*q(i); end% Recursive computation
if  n > 1A = gridsamp(range(:,2:end), q(2:end));  % Recursive call[m p] = size(A);   q = q(1);S = [zeros(m*q,1) repmat(A,q,1)];y = linspace(range(1,1),range(2,1), q);k = 1:m;for  i = 1 : qS(k,1) = repmat(y(i),m,1);  k = k + m;end
else    S = linspace(range(1,1),range(2,1), q).';
end