【441】排列硬币（暴力迭代、二分查找、牛顿迭代）

写在前面：本博客仅作记录学习之用，部分图片来自网络，如需使用请注明出处，同时如有侵犯您的权益，请联系删除！

题目描述

总共有 n 枚硬币，并计划将它们按阶梯状排列。对于一个由 k 行组成的阶梯，其第 i 行必须正好有 i 枚硬币。阶梯的最后一行可能是不完整的。给你一个数字 n ，计算并返回可形成 完整阶梯行 的总行数。

示例1	示例2

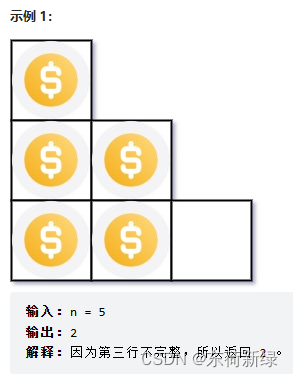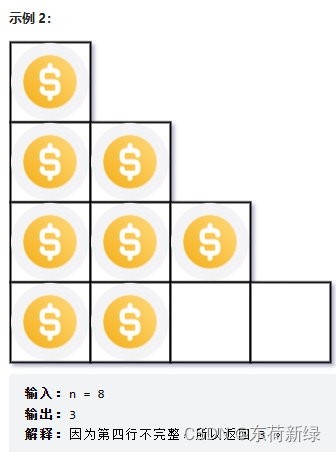解决思路

• 暴力迭代：重头开始计算所需的硬币数，本身是一个等差数列的求和问题，当计算当前层所需总量小于总硬币时返回层数。或者计算所需的硬币数小于层数k，满足
• • sum(i)<sum(k)<=sum(j)，k=i或者j
• • sum = (i+1)*i/2
• 二分查找：所需的所需的层数本质上是自然数序列，在（1-n）寻找一个层数k使得满足上述的式子，使得时间复杂度将为O(logn)
• 牛顿迭代：数学上需要计算(i+1) * i / 2 = n，本质就是需要计算该方程的根，随机给定一个尝试的解x0，不断的在上述f(x0)处做切线，再在切线与坐标轴橡胶与x1，再在f(x1)切线，不断重复上述的步骤，指导得到xi近似的满足上述式子，得到一个近似的解，取整数后得到所求的层数。

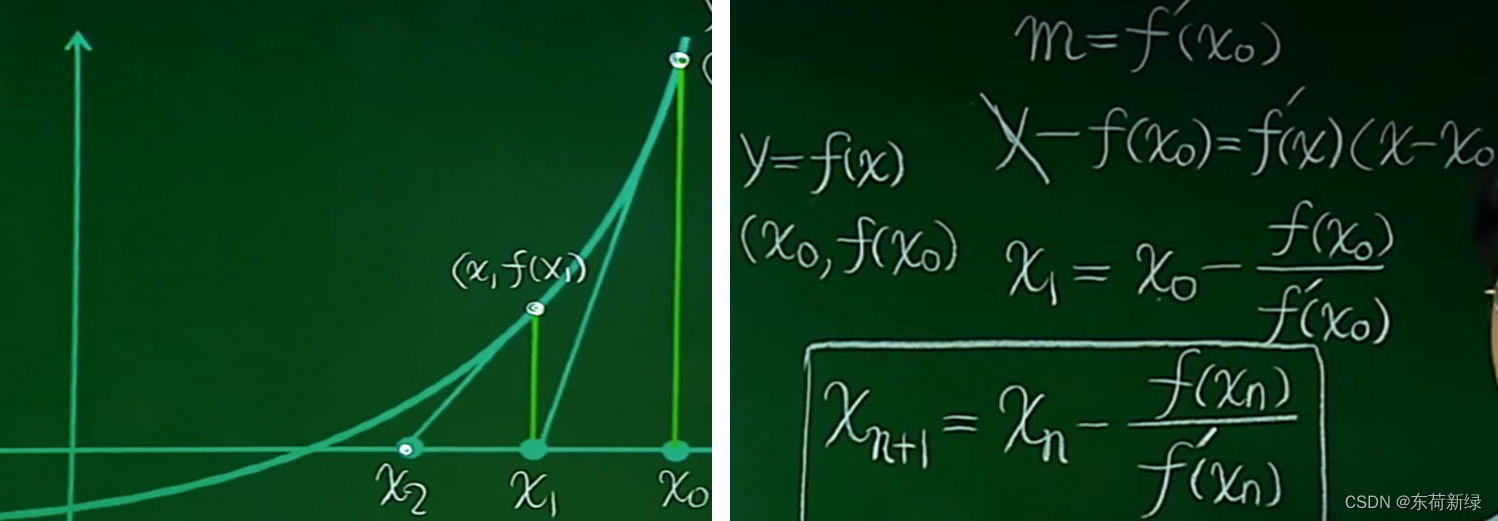
代码

暴力迭代

• 时间复杂度：O(n)
• 空间复杂度：O(1)

// 暴力迭代
class Solution {
public:// 时间复杂度：O(n)// 空间复杂度：O(1)int arrangeCoins(int n) {if(n==1) return n;for(int i=1; i<=n; i++){n = n - i;if(n<=i){return i;}}return 0;}
};//乘积可能 会溢出int的范围，使用long long
class Solution {
public:// 时间复杂度：O(n)// 空间复杂度：O(1)int arrangeCoins(int n) {int k = 0;for(int i=1; i<=n; i++){if((long long)i*(i+1)==(long long)2*n){k = i;break;}else if((long long)i*(i+1)>(long long)2*n){k = i-1;break;}}return k;}
};

二分查找

• 时间复杂度：O(logn)
• 空间复杂度：O(1)

//二分查找
class Solution {
public:// 时间复杂度：O(logn)// 空间复杂度：O(1)int arrangeCoins(int n) {int front = 0;int end = n;while(front<=end){long long mid = front+(end-front)/2;long long cost = (mid+1)*mid/2;if(cost>n){end = mid-1;}else if(cost<n){front = mid+1;}else{return mid;}}return front-1;}
};

牛顿迭代

• 迭代次数取决于起始值
• 由于是近似求解，因此对于无理数或者精度要求较高的解会导致迭代次数过多而超出时间限制。因此只考虑相对两根相等条件是不够的，需要加上两根的距离，距离足够小时，整数求解已然够了。

class Solution {
public:int arrangeCoins(int n){return (int)sqrt(n, n);}double sqrt(double x, int n) {// (x + n/x)/2->  (x + (2n-x)/x)/2double res = (x + ((double)2*n-x)/x)/2;if(x==res){return res;}else{return sqrt(res, n);}}
};

可以看到，两根相等会导致超时，这是因为迭代仅仅去寻找和期望值相等的根，会导致需要多次迭代，相反如果求根的两个近似根距离足够近，对取整就已经够了，没必要进一步的迭代寻找和期望值相等的根。

class Solution {
public:int arrangeCoins(int n){return sqrt(n, n);}int sqrt(double x, int n) {// (x + n/x)/2->  (x + (2n-x)/x)/2double res = (x + ((double)2*n-x)/x)/2;double diff = x - ((double)2*n-x)/x;if( x==res || diff < 0.001){// 3+diff，3+2diff --》3if((int)x==(int)res){return res;}else{// 3，3-diff--》2if((int)x==x){return min(x, res);}else{// 3+diff，3-diff,diff 足够小，基本上就能避免这种情况return max(x, res);}}}else{return sqrt(res, n);}}
};

致谢

欲尽善本文，因所视短浅，怎奈所书皆是瞽言蒭议。行文至此，诚向予助与余者致以谢意。