本文主要是介绍高级人工智能之自编码器Auto-encoders,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- Traditional (Vanilla/Classical) Autoencoder
- Variational Autoencoder
- Kullback–Leibler divergence
- Reparameterization
这章讲述模型框架和概念的时间较多,好像并没有涉及过多的运算,重在一些概念的理解。
Traditional (Vanilla/Classical) Autoencoder
传统的自编码器常用来进行图像去噪的任务,需要了解其模型架构和流程。
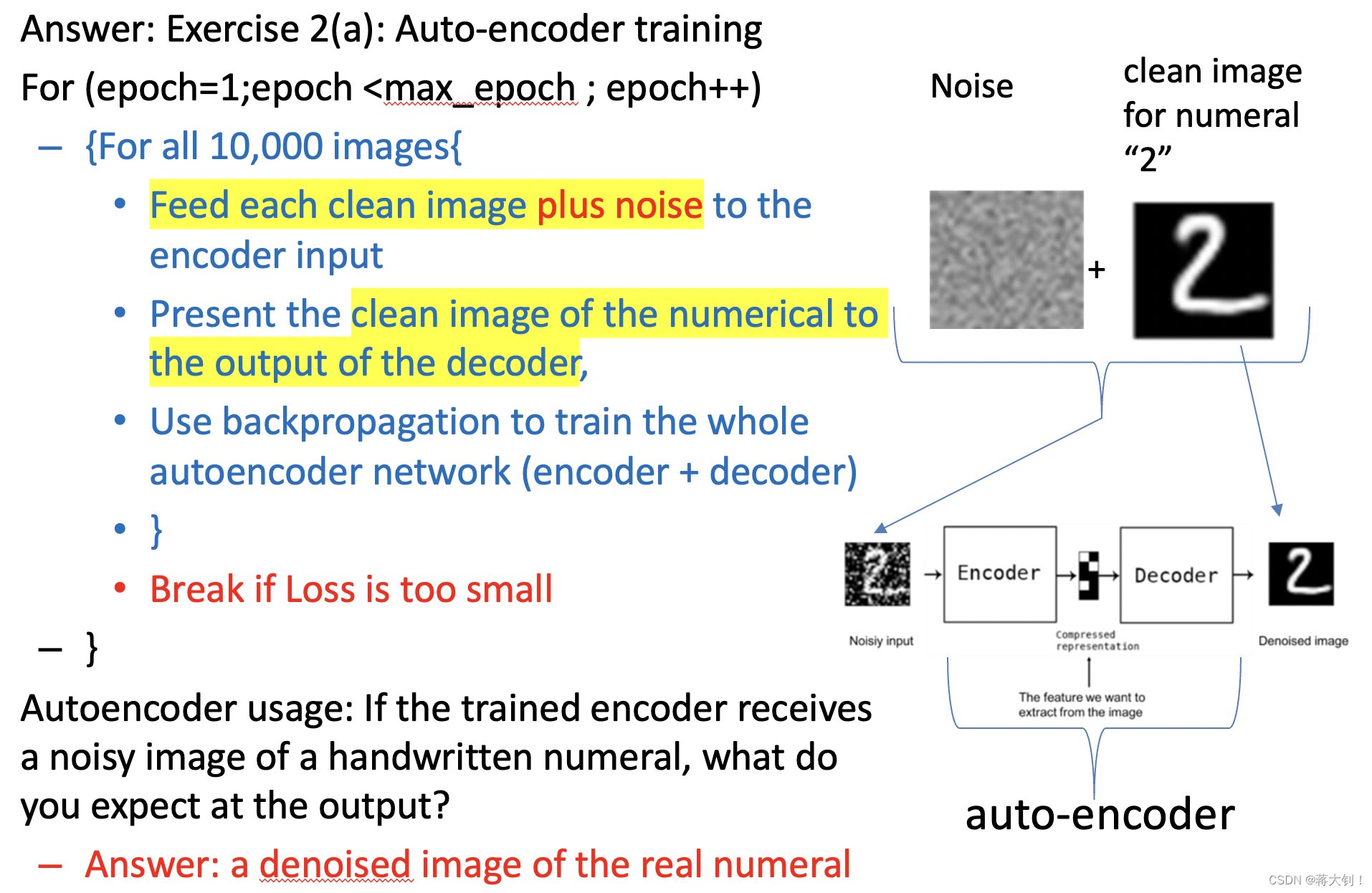
自编码器由两部分组成:从Noisy Input到Z称为编码器,从Z到De-noised Output称为解码器。Input和Output有着相同的维度。

自编码器针对输入数据X进行重建,其目的是让X的重建误差最小,这样子能保证输入和输出尽可能地相似。

Auto-encoder的训练是一个无监督学习的过程,因为并不需要标记的数据训练。流程如下所示,它将纯净的图像+噪声整体两组数据同时放入Encoder的Input,同时也将纯净的图像放入Decoder的Output,将前向传播训练得出的图像与之前被放在输出口的纯净图像计算误差,从而可以进行反向传播训练。
Variational Autoencoder
Variational Autoencoder会从输入的图像中学习概率分布的参数,然后通过这些参数来产生新的图像。从输入的图像X中学到概率分布的变量 μ \mu μ和 σ \sigma σ,这两组参数分别从hidden-mean-neurons和hidden-variance-neurons中得到, Z Z Z从 μ \mu μ和 σ \sigma σ组成的多元高斯分布中随机取样得到,接着放入Decoder进行重建。

其训练过程同Auto-encoder一致,在去噪任务中,将噪声图像放入input,纯净图像放入output,通过反向传播进行训练。
其中的关键在于反向传播过程中Loss损失的定义,损失的定义中有两项,先对相关参数进行定义,
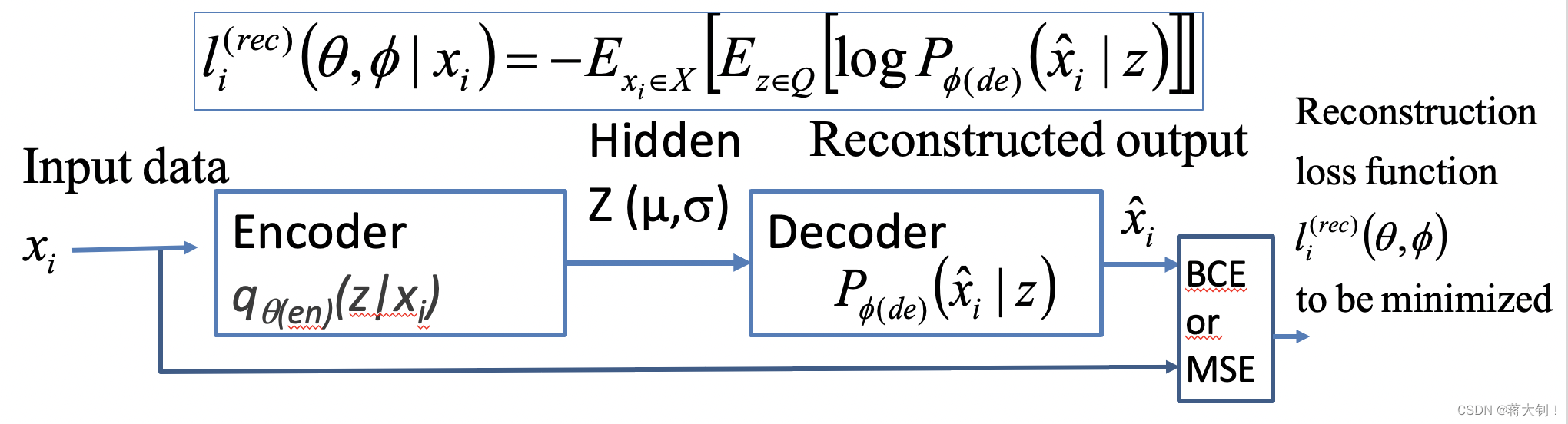
q θ ( e n ) ( z ∣ x i ) q_{\theta(en)}(z|x_i) qθ(en)(z∣xi) 表示接受输入数据 x i x_i xi,返回潜在变量 Z Z Z的概率, Z Z Z是从 μ \mu μ和 σ \sigma σ组成的多元高斯分布随机产生的, θ ( e n ) \theta(en) θ(en)代表encoder的weights和bias。
P ϕ ( d e ) ( x ^ i ∣ z ) P_{\phi(de)}(\hat x_i |z) Pϕ(de)(x^i∣z)表示接受潜在变量 Z Z Z产生的Sample,得到输出为 X ^ \hat{X} X^的概率, ϕ ( d e ) \phi(de) ϕ(de)代表decoder的weights和bias。
重建的损失 l i ( θ , ϕ ) = − E x i ∈ X [ E z ∈ Q [ l o g P ϕ ( d e ) ( x ^ i ∣ z ) ] ] l_i(\theta,\phi)=-E_{x_i \in X} \big[E_{z \in Q}[log P_{\phi (de)}(\hat x_i | z)]\big] li(θ,ϕ)=−Exi∈X[Ez∈Q[logPϕ(de)(x^i∣z)]]需要尽可能地小。由于 P P P为高斯分布,因此可以对上式重写为= 1 N ∑ x i ∈ X ( 1 2 σ x i ^ ∣ z 2 ( x i − μ x i ^ ∣ z ) 2 ) \frac{1}{N}\sum\limits_{x_i \in X}\Big( \frac{1}{2 \sigma^2_{\hat {x_i}|z}}(x_i - \mu_{\hat{x_i}|z})^2\Big) N1xi∈X∑(2σxi^∣z21(xi−μxi^∣z)2).
Kullback–Leibler divergence
但是会存在的问题是,虽然整体 l i ( θ , ϕ ) l_i(\theta,\phi) li(θ,ϕ)较小, q θ ( e n ) ( z ∣ x i ) q_{\theta(en)}(z|x_i) qθ(en)(z∣xi)和 P ϕ ( d e ) ( x ^ i ∣ z ) P_{\phi(de)}(\hat x_i |z) Pϕ(de)(x^i∣z)的差异却很大,原因显然是因为它们来自不同的概率分布。因此这里引入了Kullback–Leibler divergence 来衡量两个分布的差异程度,进而 D K L [ q θ ( e n ) ( z ∣ x i ) ∣ ∣ ( N ( 0 , I ) ] D_{KL}\big[ q_{\theta(en)(z|x_i)} || ( N(0,I)\big] DKL[qθ(en)(z∣xi)∣∣(N(0,I)]衡量了产生图像的分布与标准高斯分布的差异。
最终该模型的Loss定义为 L ( a l l ) = 1 N ∑ x i ∈ X ( 1 2 σ x i ^ ∣ z 2 ( x i − μ x i ^ ∣ z ) 2 ) + D K L [ q θ ( e n ) ( z ∣ x i ) ∣ ∣ ( N ( 0 , I ) ] L^{(all)}=\frac{1}{N}\sum\limits_{x_i \in X}\Big( \frac{1}{2 \sigma^2_{\hat {x_i}|z}}(x_i - \mu_{\hat{x_i}|z})^2\Big)+D_{KL}\big[ q_{\theta(en)(z|x_i)} || ( N(0,I)\big] L(all)=N1xi∈X∑(2σxi^∣z21(xi−μxi^∣z)2)+DKL[qθ(en)(z∣xi)∣∣(N(0,I)],其物理意义为,在局部的概率分布中,输出与输入之间的误差要尽可能小。

Reparameterization
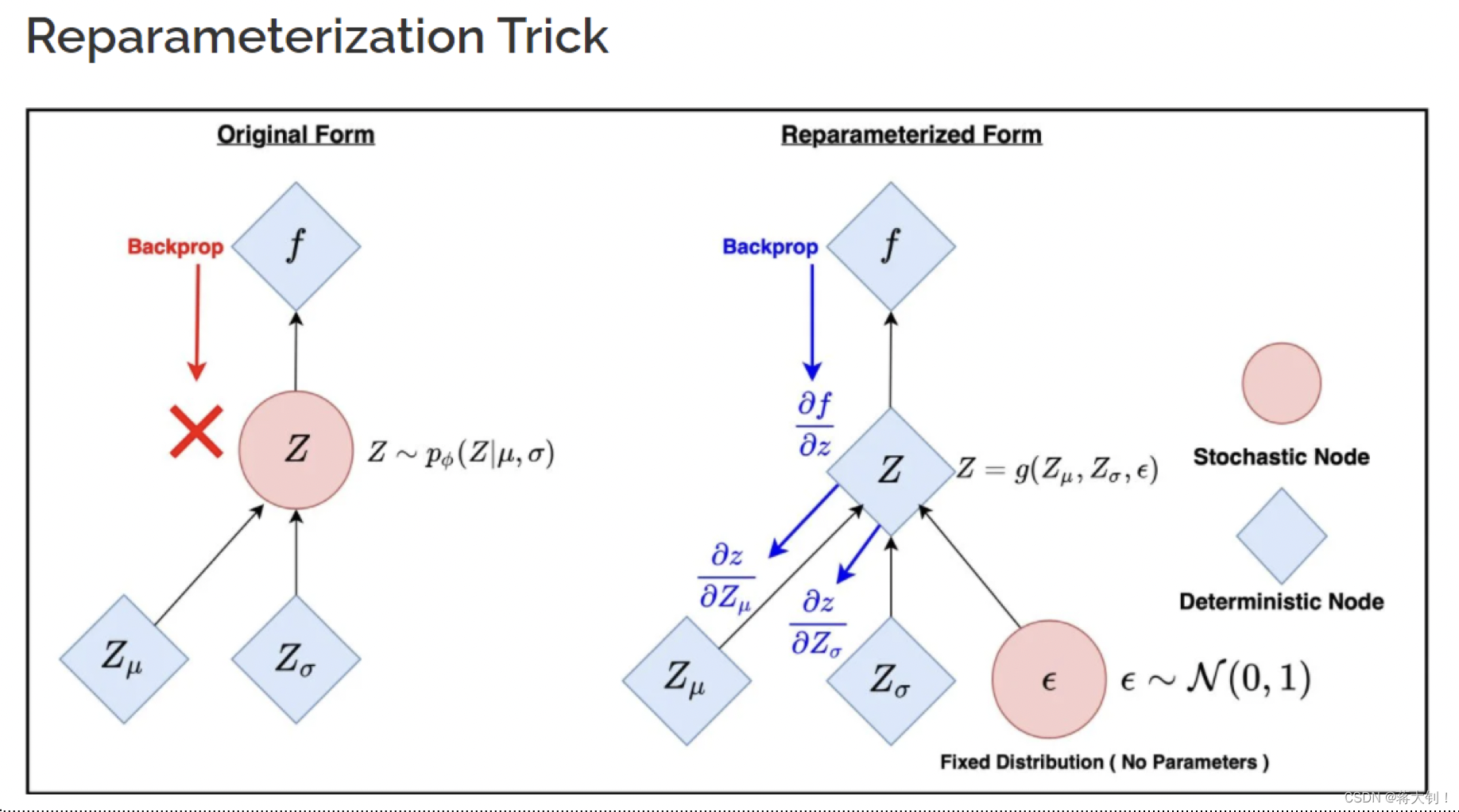
在模型构建的过程中,潜在变量 Z Z Z在 μ \mu μ和 σ \sigma σ固定的情况下涉及了随机选择样本点sample的过程,这种随机性导致了不能通过具体的公式来进行反向传播训练,因此引入了reparameterization trick,将随机化进行定量表示. 其将原先平均值为 μ \mu μ,标准差为 σ \sigma σ的高斯分布,表示为 Z = ϵ ⋅ σ x + μ x Z= \epsilon\cdot\sigma_x +\mu_x Z=ϵ⋅σx+μx,其中 ϵ ∈ N ( 0 , 1 ) \epsilon \in N(0,1) ϵ∈N(0,1),这样子任意的 Z Z Z都可以通过对 N ( 0 , 1 ) N(0,1) N(0,1)的缩放表示出来。

该方法让原先随机化的过程确定化,从而能够进行backpropagation.
这篇关于高级人工智能之自编码器Auto-encoders的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



