本文主要是介绍整理总结:深入浅出统计学——分散性和变异性的量度,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
参考资料:电子工业出版社的《深入浅出统计学》
前言
平均数能让我们知道数据集典型值——数据中心所在处,但若要给数据下具体的结论,则还是缺少足够的信息。通过分析各种距和差,来判断数据集离平均值的波动程度。
本篇目录
- 参考资料:电子工业出版社的《深入浅出统计学》
- 前言
- 具体内容
- 一、全距
- 二、迷你距
- 1、四分位距
- 2、百分位距
- 三、箱线图
- 四、方差和标准差
- 五、标准分
- 六、图形的鉴别
具体内容
一、全距
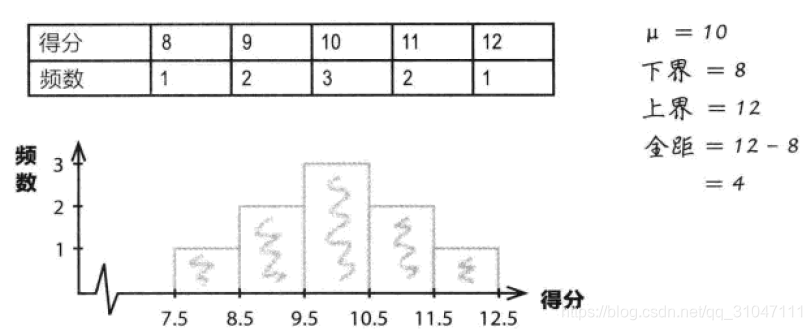
1、通过计算全距,我们可以轻易获知数据分散情况。全距可以指出数据的扩展范围,类似于测量数据的宽度。
2、计算方法是通过用数据集中的最大数减去数据集中的最小数。其中最小值称为下界,最小值称为上界。
3、优点是计算十分简单。
4、缺点是仅仅描述了数据的宽度,没有描述数据在上下界之间的分布形态,难以得出数据的真实分布形态。当存在异常值时,可能导致全距过大,即易受异常值的影响。
二、迷你距
不再度量整个数据集的全距,而是度量中央部分数据集的全距,通过迷你距可以有效忽略异常值的存在。而通过一个统一的方法来对数据集进行划分,将有助于我们确保多批数据集处理时所有都是以相同的方式忽略了异常值。

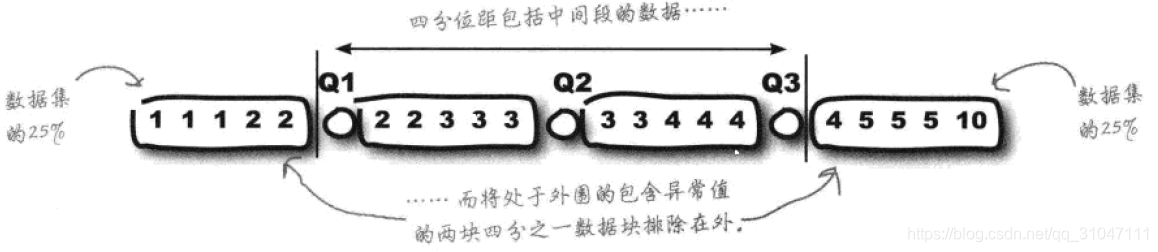
1、四分位距
1、计算步骤是通过将数据进行升序排列,选取其中三个特定位置的数据点来四等份数量划分数据集,并从左到右的称三个点叫作下四分位数、中位数和上四分位数,而四分位距的值便是上四分位数减去下四分位数的差。
2、优点是由于剔除掉头尾各1/4的数据——较小和较大的那一批数据,因此自然而然得把作为极大值或极小值的异常值也一同排除在外了。
3、意义是可以对几个数据集进行比较且比较结果不会被异常值扭曲。
4、下、上四分位数的位置的快速计算方法如下


2、百分位距
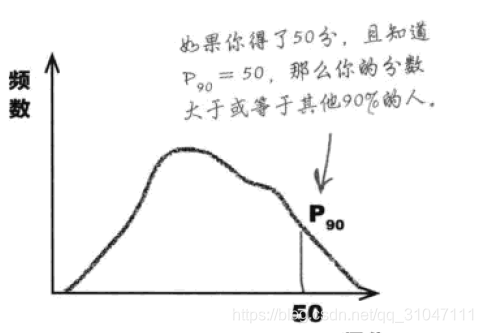
1、如果我们将一批数据分成一百份的话,那么起分割作用数值就被称作百分位数,通常,第K百分位数就是位于数据范围K%处的数值,常用Pk表示。
2、百分位距不太常用,但对于划分名次、排行却很用有,比如一场考试中第90百分位数是50分,那么可以推测出50分高于等于其他90%的人的分数。
3、计算步骤如下

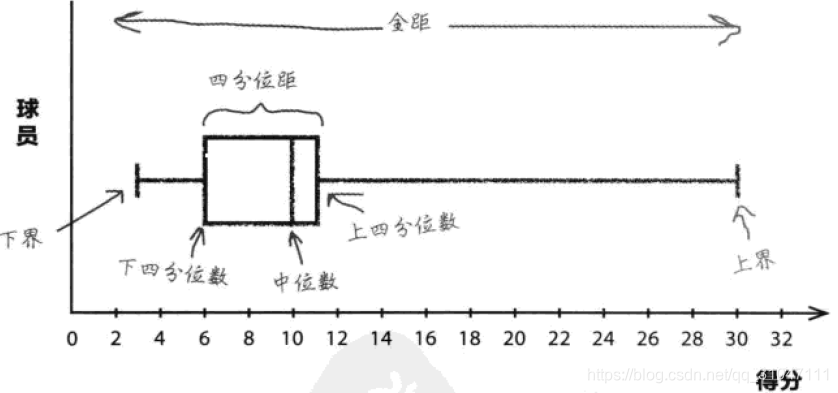
三、箱线图
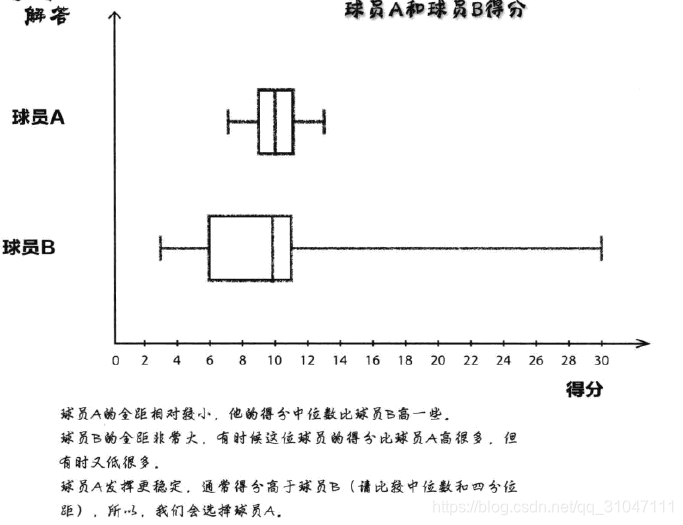
1、箱线图是一种专门显示各种各样的距的图形,它可以用直观的方法比较多批数据的全局、四分位距和中位数。
2、计算步骤如下
四、方差和标准差
1、方差是量度数据分散性的一种方法,是数值与均值的距离的平方数的平均值。 δ 2 = ∑ ( x − u ) 2 n {\delta}^2=\frac{\sum {(x-u)}^2}{n} δ2=n∑(x−u)2
2、标准差通过与均值的距离来指出分散性,比方差更加直观。 δ = ∑ ( x − u ) 2 n \delta =\sqrt{\frac{\sum {(x-u)}^2}{n}} δ=n∑(x−u)2
3、标准差的计量单位与相应数据的单位一致,即若以“厘米”进行计量,当标准差为1时,表示在典型情况下,数值与均值相距1厘米。
4、当数据均相等时,标准差为0。
五、标准分
1、通过标准分使多批数据集转化成一种统一通用的分布,进而可以对不同数据集的数据进行比较,而这些不同数据集特性可以互不相同,比如各均值和标准差各不相同。 z = x − u δ z=\frac{x-u}{\delta} z=δx−u
2、通过标准分来判断球员在自身历史数据中发挥的如何,是超长发挥还是发挥失利,同时可以判断两个球员的发挥进行比较。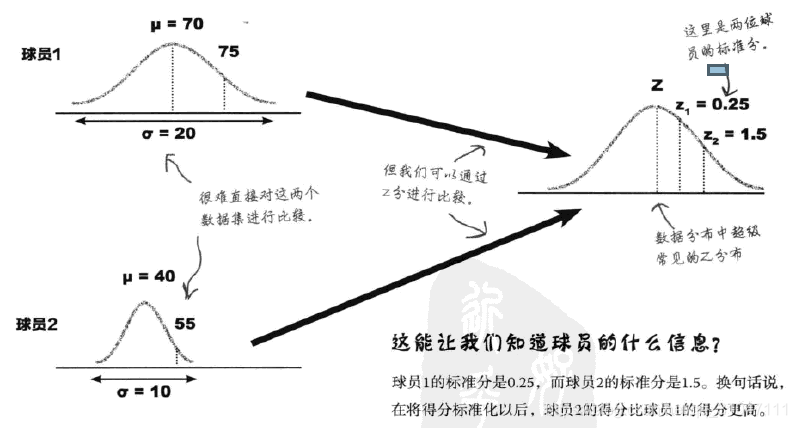
六、图形的鉴别
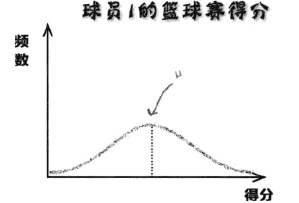
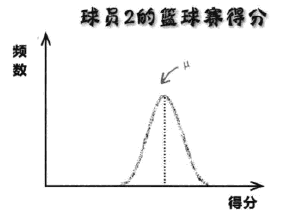
左图相较于右图而言更加宽阔,这表明其数据大多与均值相距甚远,左图对应的球员1发挥的稳定性不如球员2,具备更多的不可确定性,难以预测他在将来某一场球赛的发挥。
这篇关于整理总结:深入浅出统计学——分散性和变异性的量度的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







