资料分析-速算技巧

一、加法技巧

1. 尾数法

适用范围：多个数字的精确求和或求差。为保证精确与速度，一般可观察两位。
补充：四个选项最后一位都不一样，求最后一位就行。若有一样的，则求两位。

2. 高位叠加

适用范围：从高位加起，非精确求和或没有选项可以参考时，可以选用高位叠加法。
注意：加起来小于10时用0占位

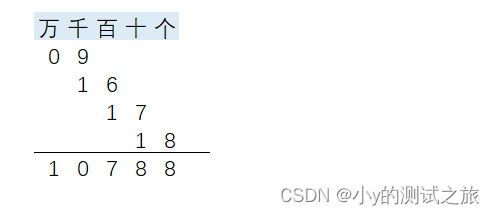
例1：计算1256、3451、1222、4859的和。

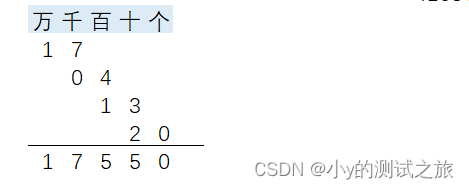
例2：计算4103、2058、3156、8233 之和。

3. 削峰填谷

适用范围：几个相近数字求和或平均值，可以先找出基准值，再根据“偏离总和”求得总和或平均值。

例1：求89、87、88、91、88、90、90、89、88、86的平均值。
解析：假设以89为基准，则89+(0-2-1+2-1+1+1+0-1-3)/10=89+(-0.4)=88.6或以88为基准，88+（1-1+0+3+0+2+2+1-2）/10=88.6

二、减法技巧

1. 整数基准法

适用场景：相邻的百位，如600多减500多
方法：被减数－减数＝（被减数－基准值）＋（基准值－减数）

例1：“632－589”，加入600 作为基准值，则632－589＝(632－600)＋(600－589)
例2：“629－386”，加入400作为基准值，则629－386=(629-400)+(400-386)

2. “21”“12”分段法

适用场景：非相邻的百位，如600多减400多
将三位数的减法分成“21”或“12”两段，尽可能保证不用借位。

例1：326-197，21分段则为：(32-19)+(6-7)=130-1=129
例2：432-226，12分段则为：(4-2)+(32-26)=200+06=206

三、乘法技巧

1. 小分互换

常用小数分数互换：

    例题1：251×784=(0.25*1000)*784=784/4=196 （251可看成4分之一，后面有多少个零无所谓，找对应答案就行）
    例题2：500×472=472/2=236（任何数乘以50，500等可以直接用数字除以2）

2. 拆分法

若乘法中有某个乘数为百分数且能拆成两个简单数值（50%、10%、5%等），我们可以将该百分数拆成两部分相乘，要擅用“1%”（“一个包子”）。
常用的小数拆分如下：
45%＝50%－5%
55%＝50%＋5%
15%＝10%＋5%
60%＝50%＋10%
95%＝1－5%
90%＝1－10% 及所有50%、100%附近的数等。

例1：468×45%=468×(50%-5%)=234-23.4=210.6 （468的50%是234，则5%则是50%小数点左移一位）
例2：362×52%=362×(50%+2%)=181+7.24=188.24 （362的百分之1是3.62，2%则是7.24）

四、除法技巧

1. 截位法

绝大多数除法都可以保留三位计算，达到速度与准度的平衡，可3 位÷3 位、3 位÷4 位、3 位÷5 位、4位÷3 位、5 位÷3 位。

2. 拆分法

拆分法具体应用：
一：如果分子在分母的50%附近，先拆出50%；
一：如果分数大小约等于1（分子分母相差不大），可先拆出100%；
三：如果分子很小，可根据实际情况拆出10%或5%或1%；
四：若通过首位判断分数在1/4、1/3 左右，可先拆1/4、1/3，此规则运用次数少，了解即可。

【50%左右】
例1：333÷642
    解析：先用642÷2=321，则分子333=321+12。则333÷642可写成321/642+12/642=50%+2%（642的1%为6.42，则12为2%不到），即52%不到。
例2：121÷292
    解析：先用292÷2=146，则分子121=146-25，则292÷2可写成146/292-25/292=50%-10%+1%=41%+ (25可写成-29+4，就可先减去10%再加1%)
例3：733÷4993
    解析：将分子分母同时乘以2，分母可看作50*2=100，分子变为1466，此时直接将小数点左移两位变为14.66%。

【100%左右】
例1：261÷292
    解析：分子写为292-31，则261÷292可写成261/261-31/261=1-11%≈89%

【1%~20%左右】
例1：33÷642
    解析：分子写成32+1，则33÷642写为5%+
例2：36÷242
    解析：分子写为24+12，则36÷242写为24/242+12/242=10%+5%=15%

3. 拓展-分子分母同时拆

利用盐水思想，将分子分母同时拆分，可以判断数字是否大于或小于某个数字。

【例2】某月共销售数量、资料1200 题6342 本，其中数量2126 本。 请判断正误：数量占比超过1/3。
2126/6342可以分子分母同时拆→（2100+26）/（6300+42） 可以可作为两部分2100/6300 和26/42 2100/6300=33.3%，因26/42 大于50%，根据盐水定性分析部分在两边 整体在中间 可以判断整体一定是在33.3%和50%+之间，所以数量占比一定超过1/3

五、ABRX四量的关系

名词解释：R增长率，X增长量，B本期/现期，A前期/基期
1、已知：A 和B，则：X=B-A，R=(B-A)/A 或 R=B/A -1
2、已知：A和X，则：B=A+X，R=X/A
3、已知：B和X，则：A=B-X，R=X/B-X
4、已知：B和R，则：A=B/(1+R)，X=B-B/(1+R)=BR/(1+R)
5、已知：A和R，则：B=A(1+R)，X=AR
6、已知：X和R，则：A=X/R，B=X/R+X

补充：今年比去年增长了30%，则今年是去年的130%，即去年的1.3倍。倍数=1+R。

六、415份数法

415 份数法是将数量关系转化为份数比例关系，从而化简计算。415 份数法中“415”分别代表基期、变化量、本期的份数。
方法：把增长率换为分数，如20%=1/5，则A:X:B=5:1:6
常用小分数互换：

例1：本期B＝455，增长率R＝16.7%，请求出前期A 和变化量X。
    解析：R=1/6，则A:X:B=6:1:7，则1份=455/7=65，X=65，A=455-65=390

例2：本期B＝680，增长率R＝40%，求变化量X。
    解析：40%换为2/5，A:X:B=2:5:7，则1份=680/7=97，X为97*2=194

例3：本期B＝694，增长率R＝-33.4%，请求出前期A 和变化量X。
    解析：R=-1/3，则A:X:B=3: -1:2，则1份=694/2=347，X=-347，A=B-X=694+347=1041

七、假设分配法

1. 核心公式：X＝AR
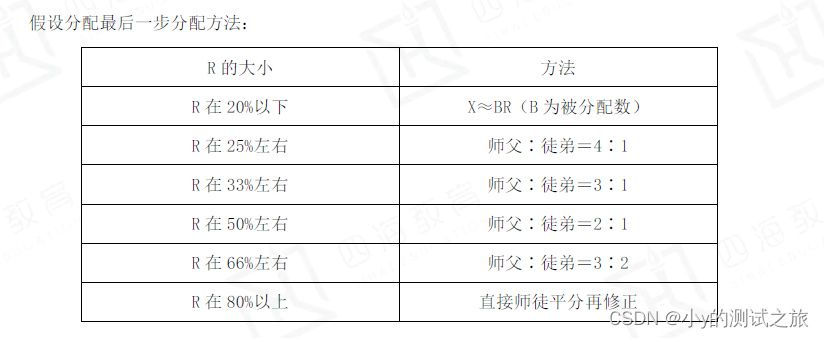
2. 使用步骤：确定分配数，画出分配树（左边是A，右边是X）。第一步用左边的AR算右边的X。最后一步时用剩余待分配数BR算出右边的X再计算左边的A，可用5%、10%等好计算的数估算后取整（粗略估算即可，误差不大）。
3. 使用时机：增长率很小（一般认为小于10%）或基期较接近整数时，最为适用。
   
4. 增长率为负数：师父要大于被分配书，师父和被分配数的正负要一致，师父和徒弟的正负要相反。
   【注】若增长率为负，被分配数接近整数时可用，如接近100、1000等，其余时候假设分配法较繁琐，不十分适用，还是建议采用直除。

例1：本期B＝543，增长率R＝5.5%，请求出前期A 和变化量X。
    解析：543先分为500和27.5（X=AR=500*5.5%），剩余15.5，15.5的5%为0.7左右，因R=5.5%，比5%稍大，因此可看作1，则15.5还剩14.5。A=500+14.5=514.5，X=28.5

例2：本期B＝1246，增长率R＝12%，请求出前期A 和变化量X。
    解析：A=1000+100+12=1112，X=120+12+2=134

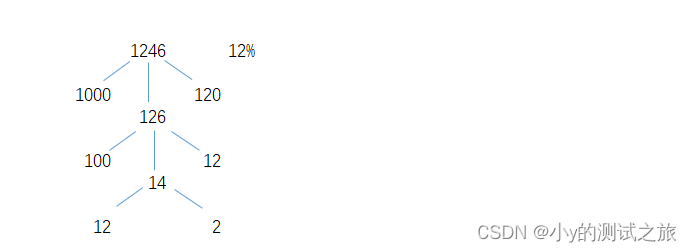
例3：本期B＝1362，增长率R＝26%，请求出前期A 和变化量X。
    解析：102分配时采用415分配法。R≈1/4，即A:X:B=4:1:5，X≈20，A≈80，即102可看作分配为80和22。所以A=1000+80=1080（R少算了，可加1为1081），X=282。

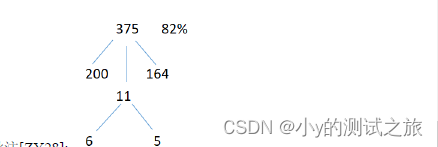
例4：本期B＝375，增长率R＝82%，请求出前期A 和变化量X。
    解析：最后一步因R是82%即一个100份，一个82份，分的差不多，只是师傅会稍微多点，直接6和5就行。

例5：本期B＝9561，增长率R＝-5.1%，请求出前期A 和变化量X。
    解析：A=10071，X=-510

思维导图：