递归基本法则简论（以斐波那契数列为例）

导言

本文假定阅读者已具备“递归思想”的基本知识，并具有用递归程序解决简单问题的能力和经验。在此基础上，本文将以斐波那契数列问题的求解作为例子，简单阐述递归的四项基本法则，给出此程序时间复杂度的数学证明，并最终优化斐波那契数列的算法。

回顾递归思想

我们熟悉的数学函数通常是由一个确定的公式描述的。与之不同的是，递归函数通过调用它自身来完成定义。这就是说，在函数的定义体内部存在函数本身。例如，一个求解斐波那契数列的递归程序如下：

		long int Fib(int N) {
/* 1*/		if (N == 0)
/* 2*/			return 0;
/* 3*/		else if (N == 1)
/* 4*/			return 1;
/* 5*/		else
/* 6*/			return Fib(N - 1) + Fib(N - 2);}

在函数Fib的定义中，第六行出现了对自身的调用。想要得到Fib（N）的值，首先必须得到Fib（N-1）和Fib（N-2）的值。

递归的基本法则

1.基准情形。必须总有某些基准情形，它无需递归就能解出。

基准情形决定了递归程序何时结束。倘若没有定义基准情形，程序将无法算出答案，陷入反复的调用中。在上述的程序中，前四行正是在定义基础情形，它规定当N<=1时直接返回，而不需要递归。这样，本递归程序才能够终止。否则程序会像奥尔加团长一样不要停下来啊！

							  |ₘₙⁿ▏n█▏　､⺍█▏ ⺰ʷʷｨ█◣▄██◣◥██████▋◥████ █▎███▉ █▎◢████◣⌠ₘ℩██◥█◣\≫██　◥█◣█▉　　█▊█▊　　█▊█▊　　█▋█▏　　█▙█ ​（来自萌娘百科）

2.不断推进。对于那些需要递归求解的情形，每一次递归调用都必须要使求解情况朝接近基准情形的方向推进。

这是说，递归程序必须严格具有朝终止方向运行的趋势。如果其中发生了循环定义等情况，程序也将无法终止。一个简单的例子是：为了求解A，我们必须首先算出B，而A的值又是计算B时必须使用的。

3.设计法则。假设所有的递归调用都能运行。

这是一条重要的法则，它说明递归是建立在假设“同一问题的所有较小实例均可以正确运行”这一前提上的。递归程序将把这些较小问题的解结合起来形成现行问题的解。这利用了数学归纳法的思想。

4.合成效益法则。在求解同一个问题的同一实例时，切勿在不同的递归调用中做重复性的工作。

“计算任何事情不要超过一次。”

前三条法则考虑了递归程序的正确性，第四条法则考虑的事情则是算法的效率问题。我们再看一次这个求解斐波那契数列的算法：

		long int Fib(int N) {
/* 1*/		if (N == 0)
/* 2*/			return 0;
/* 3*/		else if (N == 1)
/* 4*/			return 1;
/* 5*/		else
/* 6*/			return Fib(N - 1) + Fib(N - 2);}

初看起来，这个程序用非常少的代码行数正确实现了功能，给出的答案算是无懈可击的。然而，对本问题来说，这个程序并不是优秀的代码，其原因就在于它违背了递归基本法则的第四条（虽然这个代码是大一高级程序设计语言课的常客）。违背合成效益法则的后果是当输入的N非常大时（实际上小于100的数就已经够呛），这个程序的效率非常感人。这个极其简单的程序的运行时间以指数级别增长。以下是分析：

令T（N）为函数Fib（N）的运行时间。
假设T（0）=T（1）=1，为一个时间单位。
则Fib（N）函数的运行时间可表示为：（N>=2）
T（N）=T（N-1）+T（N-2）+2
（“2”表示第一行的判断和第三行的加法所消耗的时间）
又由Fib（N）=Fib（N-1）+Fib（N-2）
根据数学归纳法可知，T（N）>=Fib（N）
然后再次利用数学归纳法证明N>4时，Fib（N）>=(3/2)^N：
基准情形：N=5时，成立。
假设当N=K时成立，现证明N=K+1时成立。

Fib（K+1）=Fib（K）+Fib（K-1）
>=(3/2)^(K+1)+(3/2)^K
>=(3/2)^(K+1)*(10/9)
>=(3/2)^(K+1)

证毕。T（N）>=(3/2)^N，Fib（N）以指数级增长。

这个程序之所以缓慢，是因为重复做了大量的工作。

举例来说，当N=5时，程序首先转去计算Fib（4）和Fib（3）的值，而在计算Fib（4）时程序又会继续转去计算Fib（3）和Fib（2）。注意，此时Fib（3）已经被重复计算了两次。

计算过的信息没有被合理地保留，导致同一个数据被多次计算，浪费了大量时间。合成效益法则就是为了防止这一情况而诞生的。

如果利用一个数组存储每次计算的值，运行时间将实质性地减少。下面给出代码：

#define MAX_SIZE 100000
int a[MAX_SIZE] = { 0 };
int count_1 = 0;
int count_2 = 0;long int Fib_2(int N) {count_2++;if (N == 0)return 0;else if (N == 1)return 1;else if (a[N] == 0) {a[N] = Fib_2(N - 1) + Fib_2(N - 2);}return a[N];
}

当N=40时，两种程序的运行次数和运行时间（毫秒）比较：

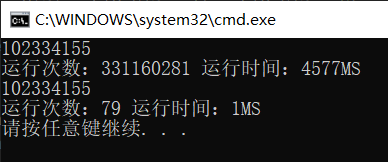
下面给出完整代码：

#include<iostream>
#include<ctime>
using namespace std;#define MAX_SIZE 100000
int a[MAX_SIZE] = { 0 };
int count_1 = 0;
int count_2 = 0;long int Fib_1(int N) {count_1++;if (N == 0)return 0;else if (N == 1)return 1;elsereturn Fib_1(N - 1) + Fib_1(N - 2);
}long int Fib_2(int N) {count_2++;if (N == 0)return 0;else if (N == 1)return 1;else if (a[N] == 0) {a[N] = Fib_2(N - 1) + Fib_2(N - 2);}return a[N];
}int main() {int n = 40;clock_t start_time_1, end_time_1, start_time_2, end_time_2;start_time_1 = clock();cout << Fib_1(n) << endl;end_time_1 = clock();cout << "运行次数：" << count_1 << " 运行时间：" << (double)(end_time_1 - start_time_1)*1000 / CLOCKS_PER_SEC << "MS" << endl;start_time_2 = clock();cout << Fib_2(n) << endl;end_time_2 = clock();cout << "运行次数：" << count_2 << " 运行时间：" << (double)(end_time_2 - start_time_2)*1000 / CLOCKS_PER_SEC << "MS" << endl;return 0;
}

总结

编写递归程序时，需要把四条基本准则牢记于心。
1.基准情形。
2.不断推进。
3.设计法则。
4.合成效益法则。
参考资料：《数据结构与算法分析：C语言描述》（第二版）