DailyPractice.2023.10.12

本文主要是介绍DailyPractice.2023.10.12，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1.[1. 两数之和]

1. 两数之和

class Solution {
public:vector<int> twoSum(vector<int>& nums, int target) {if (nums.size() == 0) return {0,0};unordered_map<int,int> mp;for (int i = 0; i < nums.size(); i++) {auto it = mp.find(target - nums[i]);if (it != mp.end()) {return {it -> second,i};}mp[nums[i]] = i;}return {-1,-1};}
};

• 时间复杂度：$O(N)$
• 空间复杂度：$O(N)$

2.[49. 字母异位词分组]

49. 字母异位词分组

class Solution {
public:vector<vector<string>> groupAnagrams(vector<string>& strs) {// 遍历每个字符串，对于每个字符串，得到该字符串所在的一组字母异位词的标志，将当前字符串加入该组字母异位词的列表中。// 遍历全部字符串之后，哈希表中的每个键值对即为一组字母异位词。vector<vector<string>> res;unordered_map<string,vector<string>> mp;if (strs.size() == 0) return res;for (auto str : strs) {string key = str;sort(key.begin(),key.end());mp[key].push_back(str);}for (auto it = mp.begin(); it != mp.end(); it ++) {res.emplace_back(it -> second);}return res;}
};

• 时间复杂度：$O(nklogk)$，其中 n是 strs中的字符串的数量，k 是 strs 中的字符串的的最大长度。需要遍历 n 个字符串，对于每个字符串，需要 O(klog⁡k)的时间进行排序以及 O(1)的时间更新哈希表，因此总时间复杂度是 O(nklog⁡k)。

• 空间复杂度：$O(nk)$，其中 n 是 strs 中的字符串的数量，k 是 strs中的字符串的的最大长度。需要用哈希表存储全部字符串。

3.[128. 最长连续序列]

128. 最长连续序列

// 对于匹配的过程，暴力的方法是 O(n) 遍历数组去看是否存在这个数，但其实更高效的方法是用一个哈希表存储数组中的数，这样查看一个数是否存在即能优化至 O(1) 的时间复杂度
// 那么怎么判断是否跳过呢？由于我们要枚举的数 x 一定是在数组中不存在前驱数x−1的，不然按照上面的分析我们会从 x−1 开始尝试匹配，因此我们每次在哈希表中检查是否存在 x−1即能判断是否需要跳过了。
class Solution {
public:int longestConsecutive(vector<int>& nums) {unordered_set<int> mp;if (nums.size() == 0) return 0;for (const int& num : nums) {mp.insert(num);}int longest = 0;for (auto num : mp) {if (!mp.count(num - 1)) {int curNum = num;int curStreak = 1;while (mp.count(curNum + 1)) {curNum += 1;curStreak += 1;}longest = max(longest,curStreak);}}return longest;}
};

• 时间复杂度：$O(n)$，其中 n 为数组的长度。具体分析已在上面正文中给出。
• 空间复杂度：$O(n)$，哈希表存储数组中所有的数需要$O(n)$的空间。

4.[283. 移动零]

283. 移动零
两次遍历：

class Solution {
public:void moveZeroes(vector<int>& nums) {if(nums.size() == 0) return;int fast = 0,slow = 0;while (fast < nums.size()) {if (nums[fast] != 0) {nums[slow ++] = nums[fast];}fast ++;}for (int i = slow; i < nums.size(); i++) {nums[i] = 0;}}
};

• 时间复杂度：$O(n)$
• 空间复杂度：$O(1)$

一次遍历：

class Solution {
public:void moveZeroes(vector<int>& nums) {// 注意到以下性质：// 左指针左边均为非零数；// 右指针左边直到左指针处均为零。// 因此每次交换，都是将左指针的零与右指针的非零数交换，且非零数的相对顺序并未改变。// 非0，交换数据，左右指针都往右移// 0，右指针右移int n = nums.size(),left = 0,right = 0;while (right < n) {if (nums[right]) {swap(nums[left ++],nums[right]);}right ++;}}
};

• 时间复杂度：$O(n)$
• 空间复杂度：$O(1)$

5.[11. 盛最多水的容器]

11. 盛最多水的容器

class Solution {
public:int maxArea(vector<int>& height) {int i = 0,j = height.size() - 1;// S(i,j) = min(h[i],h[j]) * (j - i);// 在每个状态下，无论长板或短板向中间收窄一格，都会导致水槽 底边宽度 −1 变短：// 因此，初始化双指针分列水槽左右两端，循环每轮将短板向内移动一格，并更新面积最大值，直到两指针相遇时跳出；即可获得最大面积。int res = 0;while (i < j) {res = height[i] < height[j] ?max(res,(j - i) * height[i ++]) :max(res,(j - i) * height[j --]);}return res;}
};

• 时间复杂度：$O(N)$,双指针遍历一次底边宽度 N。
• 空间复杂度：$O(1)$,变量 i , j , res 使用常数额外空间。

6.[15. 三数之和]

15. 三数之和

class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {sort(nums.begin(),nums.end());vector<vector<int>> res;if (nums.size() == 0) return res;for (int k = 0; k < nums.size() - 2; k ++) {if (nums[k] > 0) break;if (k > 0 && nums[k] == nums[ k - 1]) continue;int i = k + 1,j = nums.size() - 1;while (i < j) {int sum = nums[k] + nums[i] + nums[j];if (sum < 0) {while (i < j && nums[i] == nums[++i]);}else if(sum > 0) {while (i < j && nums[j] == nums[--j]);}else {res.push_back(vector<int>{nums[k], nums[i], nums[j]});while(i < j && nums[i] == nums[++i]);while(i < j && nums[j] == nums[--j]);}}}return res;}
};

• 时间复杂度：$O(N^2)$,其中固定指针k循环复杂度$O(N)$，双指针 i，j 复杂度 $O(N)$
• 空间复杂度：$O(1)$,指针使用常数大小的额外空间。

7.[3. 无重复字符的最长子串]

3. 无重复字符的最长子串

class Solution {
public:int lengthOfLongestSubstring(string s) {unordered_map<char, int> dic;int i = -1, res = 0, len = s.size();for (int j = 0; j < len; j ++) {// 哈希表 dic 统计： 指针 j 遍历字符 s ，哈希表统计字符 s[j] 最后一次出现的索引 。if (dic.find(s[j]) != dic.end()) {i = max(i,dic.find(s[j]) -> second);}dic[s[j]] = j; // 哈希表记录res = max(res, j - i); // 更新结果}return res;//时间复杂度 O(N) ： 其中 N 为字符串长度.//空间复杂度 O(1) ： 字符的 ASCII 码范围为 000 ~ 127 ，哈希表 dic 最多使用 O(128)=O(1)大小的额外空间。}
};

• 时间复杂度 O(N) ： 其中 N 为字符串长度.
• 空间复杂度 O(1) ： 字符的 ASCII 码范围为 000 ~ 127 ，哈希表 dic 最多使用 O(128)=O(1)大小的额外空间。

8.[206. 反转链表]

206. 反转链表

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* reverseList(ListNode* head) {if (head == nullptr) return nullptr;ListNode* cur = head;ListNode* pre = nullptr;ListNode* temp = nullptr;while (cur) {temp = cur -> next;cur -> next = pre;pre = cur;cur = temp;}return pre;}
};

• 时间复杂度：O(n)，其中 n 是链表的长度。需要遍历链表一次。

• 空间复杂度：O(1)。

9.[141. 环形链表]

141. 环形链表

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode(int x) : val(x), next(NULL) {}* };*/
class Solution {
public:bool hasCycle(ListNode *head) {if (head == nullptr || head -> next == nullptr) {return false;}// 理解成公倍数，两个正整数一定会有一个最小公倍数，这个地方就是重合点ListNode* fast = head;ListNode* slow = head;while (fast && fast -> next) {fast = fast -> next -> next;slow = slow -> next;if (slow == fast) return true;}return false;}
};

• 时间复杂度：O(N)，其中 N是链表中的节点数。
  当链表中不存在环时，快指针将先于慢指针到达链表尾部，链表中每个节点至多被访问两次。
  当链表中存在环时，每一轮移动后，快慢指针的距离将减小一。而初始距离为环的长度，因此至多移动 N 轮。

• 空间复杂度：O(1)。我们只使用了两个指针的额外空间。

10.[160. 相交链表]

160. 相交链表

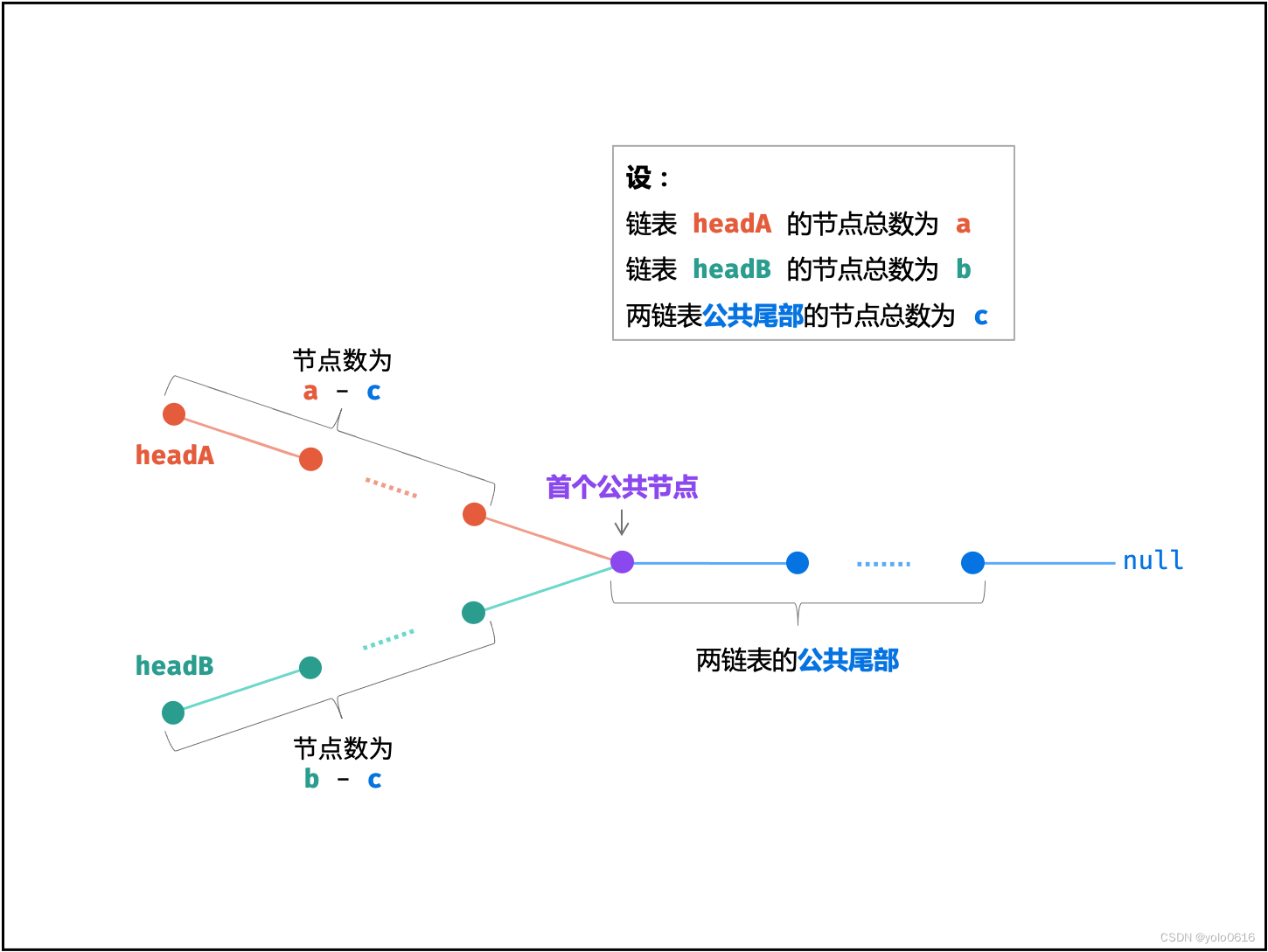
考虑构建两个节点指针 A​ , B 分别指向两链表头节点 headA , headB ，做如下操作：

指针 A 先遍历完链表 headA ，再开始遍历链表 headB ，当走到 node 时，共走步数为：
a+(b−c)
指针 B 先遍历完链表 headB ，再开始遍历链表 headA ，当走到 node 时，共走步数为：
b+(a−c)

如下式所示，此时指针 A , B 重合，并有两种情况：
若两链表 有 公共尾部 (即 c>0) ：指针 A , B 同时指向「第一个公共节点」node 。
若两链表 无 公共尾部 (即 c=0 ) ：指针 A , B 同时指向 null 。

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode(int x) : val(x), next(NULL) {}* };*/
class Solution {
public:ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {if (headA == nullptr) return headB;if (headB == nullptr) return headA;ListNode* p1 = headA;ListNode* p2 = headB;while (p1 != p2) {if (p1 == nullptr) p2 = headB;else p1 = p1 -> next;if (p2 == nullptr) p1 = headA;else p2 = p2 -> next;}return p1;}
};

• 时间复杂度 O(a+b) ： 最差情况下（即 ∣a−b∣=1| , c=0 ），此时需遍历 a+b个节点。
• 空间复杂度 O(1)) ： 节点指针 A , B 使用常数大小的额外空间。

这篇关于DailyPractice.2023.10.12的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---