深入理解拉格朗日乘子法和KKT条件的原理及运用

一、凸函数

以下讨论均基于凸优化，首先要知道什么是凸函数：
对于任意属于[0,1]的a和任意属于凸集的两点x, y，有f(tx1+(1−t)x2)≤tf(x1)+(1−t)f(x2)，几何上的直观理解就是两点连线上某点的函数值，大于等于两点之间某点的函数值。凸函数的任一局部极小点也是全局极小点。
凸集定义：欧式空间中，对于集合中的任意两点的连线，连线上任意一点都在集合中，我们就说这个集合是凸集。

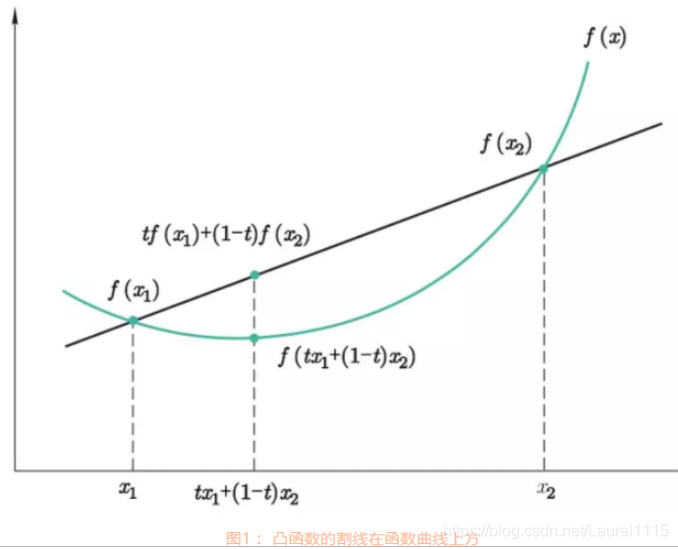
对于一元函数f(x)，我们可以通过其二阶导数f′′(x) 的符号来判断。如果函数的二阶导数总是非负，即f′′(x)≥0 ，则f(x)是凸函数。
扩展：对于凸函数，我们可以推广出一个重要的不等式，即Jensen不等式。如果 f 是凸函数，X是随机变量，那么f(E(X))≤E(f(X))，上式就是Jensen不等式的一般形式。

二、常见的三类最优化问题

1.无约束优化问题:
min f(x);
对于无约束的优化问题解决方法通常是函数对变量求导，令求导函数等于0的点可能是极值点，最后再将结果带回原函数进行验证。但是如果已经是凸函数，就不需要再验证，可以保证求导函数等于0的点是最优解。
2.有等式约束的优化问题:
min f(x),
s.t hi(x)=0;i=1,…,n
解决这类问题要运用到拉格朗日乘子法构造拉格朗日函数，将在下面详细介绍
3.有不等式约束的优化问题：
min f(x),
s.t gi (x)<=0 （i=1,…,n）
hj(x)=0（j=1,…,m）
解决这类问题要引入KKT条件并构造拉格朗日函数，将在下面详细介绍

三、拉格朗日乘子法解决带等式约束的最优化问题

（一）用实例理解拉格朗日乘子法的背后意义

1.现在假设我们有一个函数

我们要在满足

这个等式约束条件下求极小值。也就是如下式：

2.我们需要先直观的看一下函数f(x,y)以及它的等高线的图像：


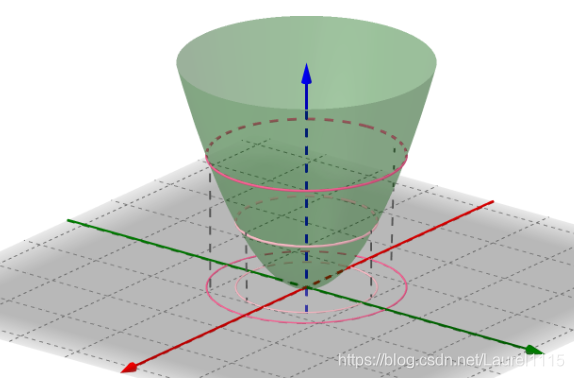
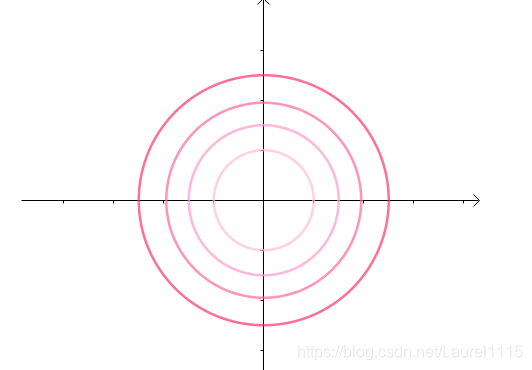
3.接下来，我们求出函数f(x,y)的梯度向量：

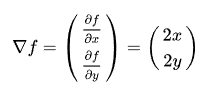
我们需要知道的是梯度向量