本文主要是介绍专题:平面、空间直线参数方程下的切线斜率问题,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
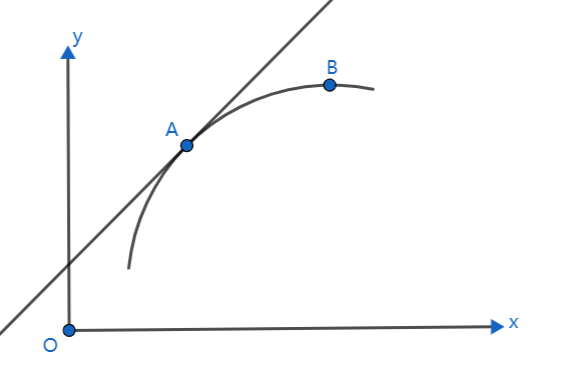
本文研究平面、空间直线在参数方程形式下,切线斜率(即导数)如何表示的问题。
如上图所示。 设 y = f ( x ) , x = φ ( t ) , y = ψ ( t ) 当 t = t 0 时, x = x 0 , y = y 0 ,即点 A 坐标为 ( x 0 , y 0 ) 点 A 处的导数 f ′ ( x 0 ) = lim Δ x → 0 Δ y Δ x = lim Δ t → 0 ψ ( t 0 + Δ t ) − ψ ( t 0 ) φ ( t 0 + Δ t ) − φ ( t 0 ) = lim Δ t → 0 ψ ( t 0 + Δ t ) − ψ ( t 0 ) Δ t / φ ( t 0 + Δ t ) − φ ( t 0 ) Δ t = lim Δ t → 0 ψ ( t 0 + Δ t ) − ψ ( t 0 ) Δ t / lim Δ t → 0 φ ( t 0 + Δ t ) − φ ( t 0 ) Δ t = ψ ′ ( t 0 ) φ ′ ( t 0 ) 因此点 A 处的切线向量可表示为 ( ψ ′ ( t 0 ) , φ ′ ( t 0 ) ) 而切线方程为 y − y 0 = ψ ′ ( t 0 ) φ ′ ( t 0 ) ( x − x 0 ) ,即 y − y 0 ψ ′ ( t 0 ) = x − x 0 φ ′ ( t 0 ) 同理可得空间直线的点向式方程为: y − y 0 ψ ′ ( t 0 ) = x − x 0 φ ′ ( t 0 ) = z − z 0 ω ′ ( t 0 ) 如上图所示。\\ 设y=f(x),x=\varphi(t),y=\psi(t) \\ 当t=t_0时,x=x_0,y=y_0,即点A坐标为(x_0,y_0) \\ 点A处的导数f^\prime(x_0)=\lim_{\Delta x \to 0}\frac{\Delta y}{\Delta x}=\lim_{\Delta t \to 0}\frac{\psi(t_0+\Delta t)-\psi(t_0)}{\varphi(t_0+\Delta t)-\varphi(t_0)} \\ \,\\ =\lim_{\Delta t \to 0}\frac{\psi(t_0+\Delta t)-\psi(t_0)}{\Delta t}/\frac{\varphi(t_0+\Delta t)-\varphi(t_0)}{\Delta t} \\ \,\\ =\lim_{\Delta t \to 0}\frac{\psi(t_0+\Delta t)-\psi(t_0)}{\Delta t}/\lim_{\Delta t \to 0}\frac{\varphi(t_0+\Delta t)-\varphi(t_0)}{\Delta t} \\ \,\\ =\frac{\psi^\prime(t_0)}{\varphi^\prime(t_0)} \\ \,\\ 因此点A处的切线向量可表示为(\psi^\prime(t_0),\varphi^\prime(t_0)) \\ 而切线方程为y-y_0=\frac{\psi^\prime(t_0)}{\varphi^\prime(t_0)}(x-x_0),即\frac{y-y_0}{\psi^\prime(t_0)}=\frac{x-x_0}{\varphi^\prime(t_0)} \\ \,\\ 同理可得空间直线的点向式方程为:\\ \frac{y-y_0}{\psi^\prime(t_0)}=\frac{x-x_0}{\varphi^\prime(t_0)}=\frac{z-z_0}{\omega^\prime(t_0)} 如上图所示。设y=f(x),x=φ(t),y=ψ(t)当t=t0时,x=x0,y=y0,即点A坐标为(x0,y0)点A处的导数f′(x0)=Δx→0limΔxΔy=Δt→0limφ(t0+Δt)−φ(t0)ψ(t0+Δt)−ψ(t0)=Δt→0limΔtψ(t0+Δt)−ψ(t0)/Δtφ(t0+Δt)−φ(t0)=Δt→0limΔtψ(t0+Δt)−ψ(t0)/Δt→0limΔtφ(t0+Δt)−φ(t0)=φ′(t0)ψ′(t0)因此点A处的切线向量可表示为(ψ′(t0),φ′(t0))而切线方程为y−y0=φ′(t0)ψ′(t0)(x−x0),即ψ′(t0)y−y0=φ′(t0)x−x0同理可得空间直线的点向式方程为:ψ′(t0)y−y0=φ′(t0)x−x0=ω′(t0)z−z0
这篇关于专题:平面、空间直线参数方程下的切线斜率问题的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





