本文主要是介绍新型肺炎确诊人数趋势拟合,兼谈数值优化方法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
更多专业的人工智能相关文章,微信搜索 : robot-learner , 或扫码

根据各大新闻媒体的报道,从2019年12月8日的第一起报道算起,截至2020年1月30日的新型肺炎累计确诊人数大概8000人。下图反映了每日累计确诊数量变化情况,和指数模型拟合的结果:
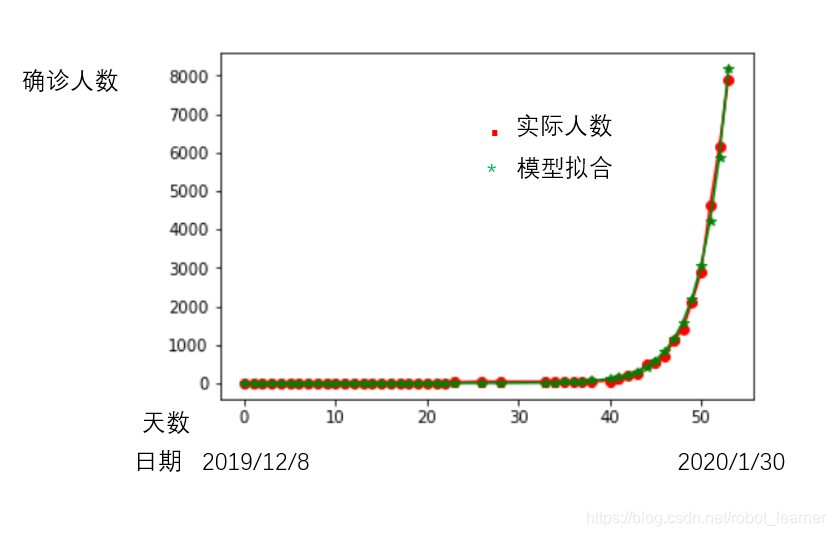
可以看出,疾病传播处于上升期,且呈明显的指数上升趋势。上图中的指数模型为下列形式:
![]()
上式中,x 为每日天数,2019/12/9号为第0天; y为每日累计确诊人数; 模型参数有两个:N0 为第0天的确诊人数; a为每日增长率。 这里我们假设人数是连续的,可以为小数。通过数值优化的方式,我们找到目前最佳的参数为:
![]()
这意味着在目前疾病传播过程中,每日新增确诊39%左右的人数。 另一方面,根据指数模型,在第26天左右,确诊人数为1个人。 这个当然不是真正的数字,但是这个时间的正好是2020年1月初,和开始出现较多确诊人数报道时间差不多。
上面的指数模型非常简单,事实上利用python中的scipy包,几行简单的代码便可以得到结果。但是背后的优化原理是有意义和通用性的。
我们可以分为下面几个步骤来理解如何通过数值优化的方式来得到上述结果:
- 最小二乘法的来源
首先如果要获得上面所诉的参数,我们可以利用最小二乘法(或最小平方和)的方法。最小二乘法的原理非常直观,符合大家通常的直觉。我们在前面的“线性回归算法原理”文章中涉及过这个解释。
假设我们有一系列测量的x和y值: (x1,y1), (x2,y2)… (xn, yn) n个数据点。这些测量值在我们疾病传播问题中可以是每天的天数 (x)和每天的累计确诊人数 (y)。另一方面我们有关于y测量值的一个理论公式y= f(x;θ) ,而公式中的参数θ可以是一个参数也可以是多个参数,并且这些参数正是我们要通过优化方法找到的目标值。
可以想象,如果我们的理论公式准确, 每天的实际测量数据 y 和通过理论公式计算出的理论值f(x) 应该非常一致,他们的差别应当趋近零。基于这个原则,最小二乘法就是要找到最佳的参数来使得下面的求和公式最小化:

换句话说,我们需要找到参数 θ 使得上面的平方和最小。
虽然最小二乘法符合人们的直觉,但是它是有统计理论根据的。这是基于统计中最大似然法估计参数得到的。只要能够找到事件发生的概率形式,最大似然拟合方法便可以给出没有偏差的参数估计结果。怎么得到疾病发生的概率形式呢? 只需要做一个简单的假设即可: 每天测量得到的确诊人数和真实的确诊人数的差别是一个均值为0的正态分布函数。可以用下式表达:
![]()
其中ε是每日确证人数y的固有误差,是一个平均值为0,方差为σ2的正态分布。换一句话说,y也符合正态随机分布函数,并且平均值为围绕理论值f(x)波动,方差为σ2。换句话说,y满足下式概率分布:
![]()
正太分布的形式在实际生活中非常普遍,比如人的身高。它必然是一个围绕着一个平均值波动的分布。下图是某地男性身高分布图,呈正太分布:
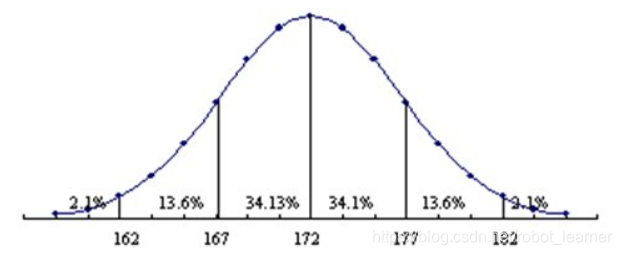
上图显示该地男性身高均值为172cm, 标准差 δ为5cm左右。 基于这两个数字,我们可以算出,该地随机找出一名男性,身高在172cm和177cm之间概率为34.1%。
有了y的概率分布函数,为了得到参数的最佳优化值,我们可以用统计学中的最大似然拟合方法,即最佳的参数就是可以把似然值最大化的参数。把n个x和y的训练数据的值带入似然值的定义,可以得到似然值的公式如下:

因为连乘的方式不利于数学运算,可以把上式取Log以后再进行运算,并且因为Log函数为单调函数,变换后的形式不会影响我们对最大值所对应的参数判断。
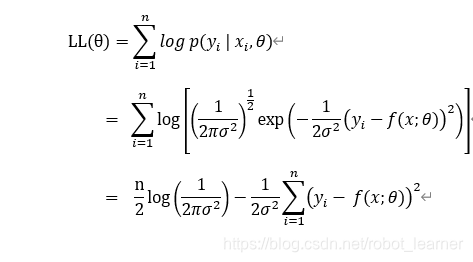
从上式可以看出,因为![]() 为不变的常数,寻找似然公式LL(θ)最大值等价于寻找下式的最小值:
为不变的常数,寻找似然公式LL(θ)最大值等价于寻找下式的最小值:

到了这一步,可以看出最小二乘法的形式:测量值和预测值差别的平方和最小化形式。
- 信赖域(trust region)优化原理
上面讲到的最小二乘法公式给了我们要优化(或者最小化)的目标函数。但是如何寻找最佳参数使得上面公式最小化仍然不清楚。
对微积分熟悉的读者肯定知道,要找到一个函数的极值,满足一定条件下,函数的一阶导数为零时候,对应的参数即为最佳值。但是这个方法在实际问题中通常难以应用,因为很多实际问题都没有解析解。因此我们需要通过数值的方法来搜索最佳值。
那可以想到的最简单的方法就是grid search,如果我们把参数空间分成许多很细的格子。沿着每个格子依次计算当前函数的值,直到遇到函数的极值点为止。但这个方法的问题在于搜索空间太大,实际问题中不能有效应用。
因此通常有效的搜索策略有两种:一种叫线搜索 (line search),另一种叫做信赖域(trust region)。机器学习很多算法中遇到的梯度下降算法其实就是一种线搜索。 梯度下降优化的原理我们在后面的文章会介绍。这里我们先介绍信赖域的优化方法。
线搜索和信赖域的比较可以用这样一个例子来说明。我们站在北京西单的位置,但是想要去天安门(注:天安门在西单东边3km左右)。线搜索的策略就是,我们首先可能沿着北边寻找。走了一段距离发现不对,可能离天安门越来越远。于是调整方向,接着沿着东南方向寻找,最终找到天安门。 而信赖域的策略是这样:我们首先确定一个半径,比如我们肯定天门肯定在6km范围。我们在半径6km的距离内仔细寻找,结果可能发现走过了头,找到了更东边的王府井。于是重新调整半径为4km,最终找到了天安门。
信赖域优化方法的核心问题在于用一个二次的方程去近似当前搜索参数所在的位置,这样一个二次方程便构成了一个信赖域用来寻找当前的最佳参数所在位置。当然随着参数位置的搜索移动,这个二次方程的范围不断通过反馈动态的调整。
具体来说,参数待优化的函数在第k次迭代中f(x;θ) 可以用泰勒函数二阶形式展开,从而用二次项来近似原函数:
![]()
上式中mk就是二次函数用来近似 第k次迭代时候的原函数,从而把原函数的优化转化为更加简单的二次方程,从而迭代搜索最佳参数解。
这篇关于新型肺炎确诊人数趋势拟合,兼谈数值优化方法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




