本文主要是介绍MRI k空间概念整理,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
以下内容为MRI期末复习笔记,仅供复习参考使用。
K空间概念
K空间为包含MR数据的阵列,也可定义为原始数据阵列相位编码轴和频率编码轴的交叉点
·MR扫描得到的数据为谱空间数据,谱空间数据与空间数据位置无直接对应关系
·k空间每一数据点或数据线都包含着整个图像的信息
·数据点与施加的不同场强有关(静磁场和梯度场的叠加)梯度场分为相位编码梯度场和频率编码梯度场
·k空间上半部和下半部为共轭对称,即两端相位编码梯度场幅度相等,极性相反(对称性)
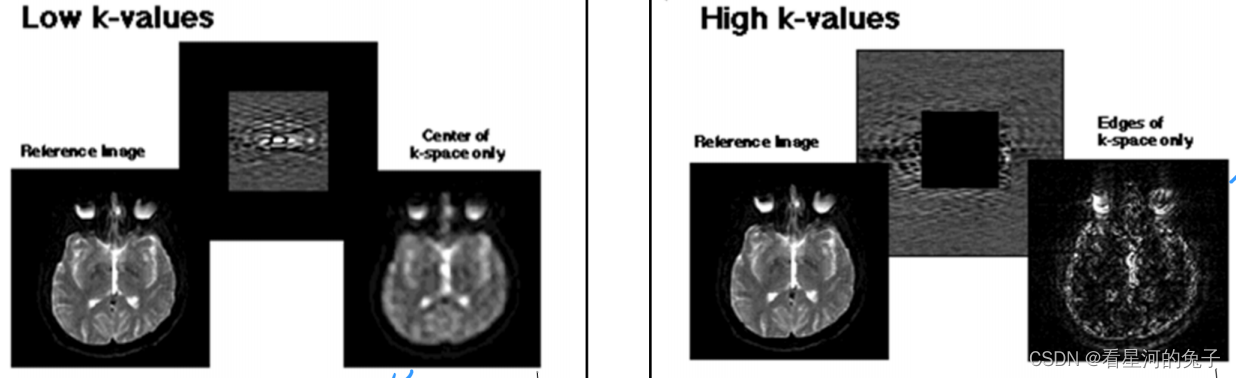
·k空间中心的信号比外围信号高,对图像对比度影响大;外围信号低,对空间分辨力影响大
·k空间中央包含最大信号
| 分析 | |
|---|---|
| 中央行有信号峰最大值 | 当相位编码为y方向,中央行是在没有相位编码影响下获得的,没有产生散相,中间为0相位(可参照下面k空间的填充方式) |
| k空间的中央列对应每个回波信号的波峰 | 当自旋完全相位重聚时达到最大幅度(回波峰),则每行数据的中心对应每个回波的中心 |
| 梯度场对信号的影响 | Gp和Gf都是中间值小、两边值大,使采集的信号呈现出中间信号高,四周信号低 |
| 高幅度梯度场:低信号,差异大——空间分辨率好 | |
| 低幅度梯度场:高信号,差异小——信噪比好 |
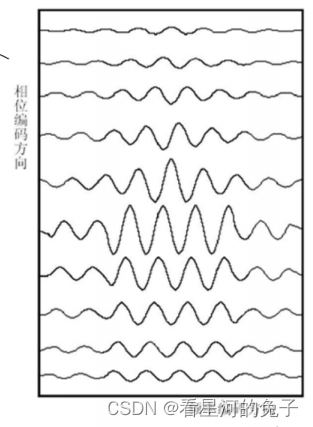
k空间的填充方式
【一般要求至少有65%的k空间得以填充,对于大多数标准成像,要求填充全部k空间。
完全填充k空间一次的情况叫1NEX或1NAQ,当只有部分K空间填充时,叫做部分NEX。】
相位编码填充方式:Gp由负最大幅度向正最大幅度变化
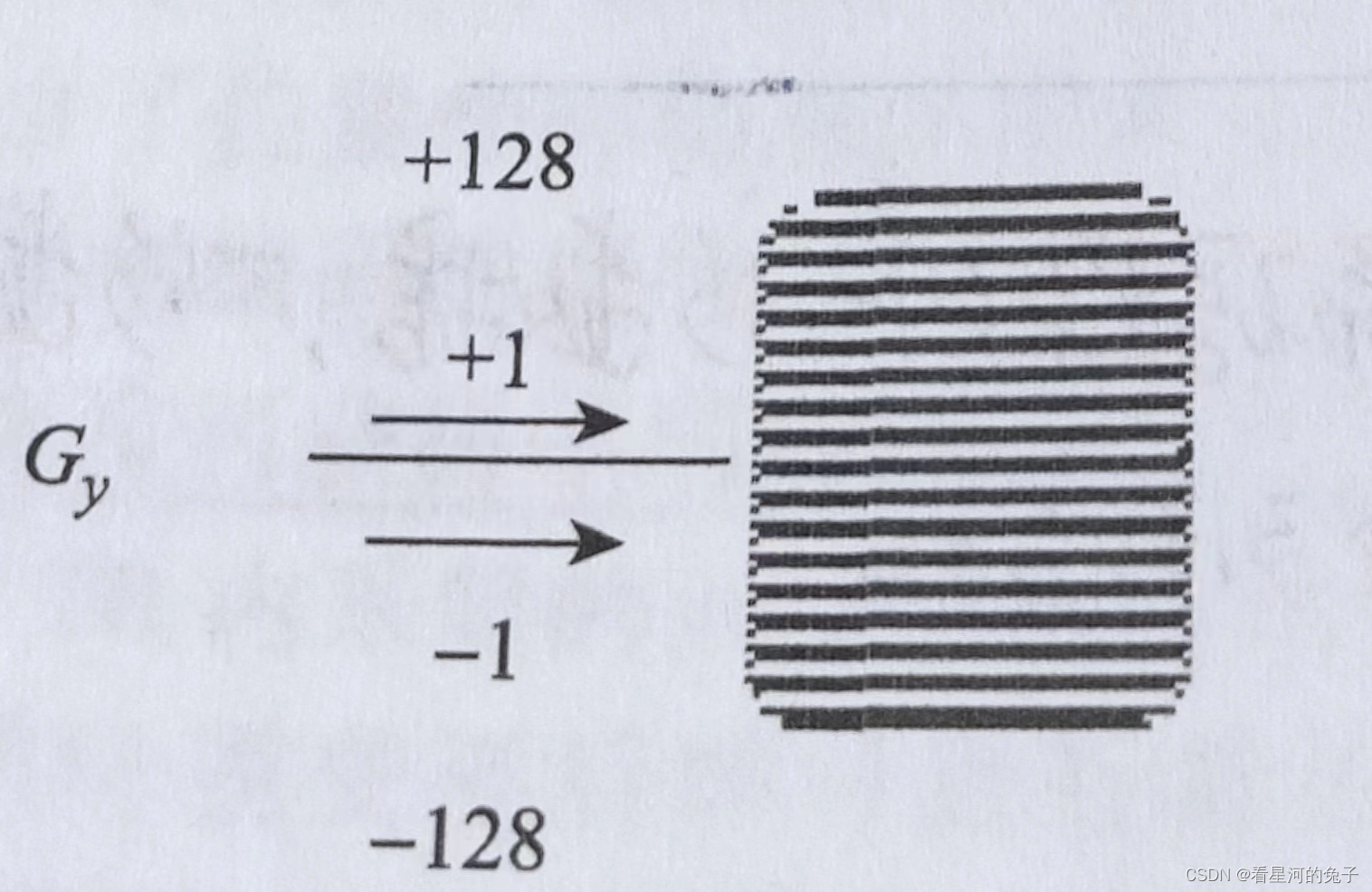
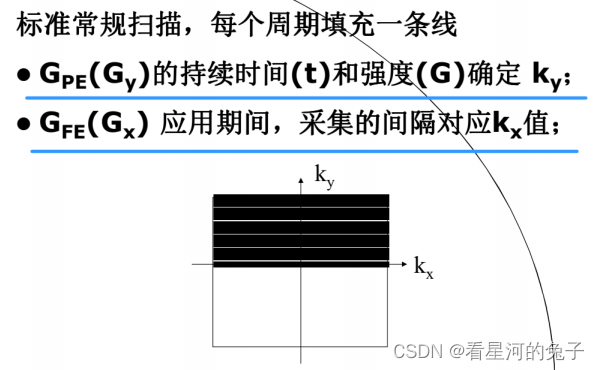
举例:SE序列:每一个TR(脉冲序列重复时间)填充k空间中的一条线,若要求256相位编码,则执行256次
其次,k空间有多种填充方式,不一定是顺序填充,具体看序列优化要求
部分NEX
- 根据 K 空间数据的共轭对称性进行重建,只利用部分的行数据(1/2 NEX,1/4 NEX),⼀般需要采集一半多
⼀些的数据进行相位校正,并且中央行必须要采集到 - 提高了速度,但是 SNR 信噪比没有增加(可能下降),伪影增加,图像对比度没有变化(因 TE 和 TR 没有
变化) - ⼀般用于定位像
部分回波
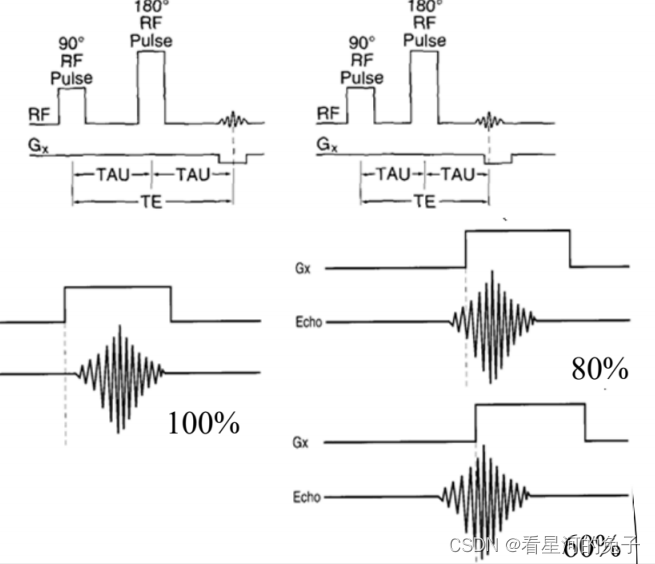
- 每个回波信号只采集了⼀部分(大于 50%),未采集的部分利用采集的部分的共轭对称性进行重建,可以使
TE 更短,但 TR 不变 - 速度没有变化,降低了 TE 时间,对于早期的回波能够提高 SNR,抑制 T2W 图像,降低流动伪影和磁敏感
效应 - ⼀般用于获得 T1W 图像,降低流动伪影和磁敏感效应的情况下
TE缩短的解释:对回波没有采集完全,如上图所示,每行数据并没有采集满
两个技术的对比
| 部分NEX | 部分回波 | |
|---|---|---|
| speed | 提高 | 不变 |
| 对比度 | 不变 | T 2 T_2 T2下降 |
| SNR | 不变或下降 | 会提高也可能不变 |
| 伪影 | 增加 | 降低流动伪影和磁敏感伪影 |
其他填充方式
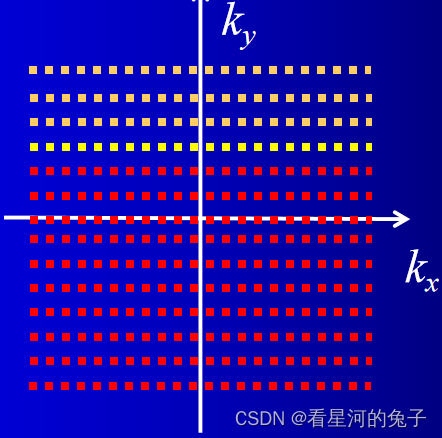
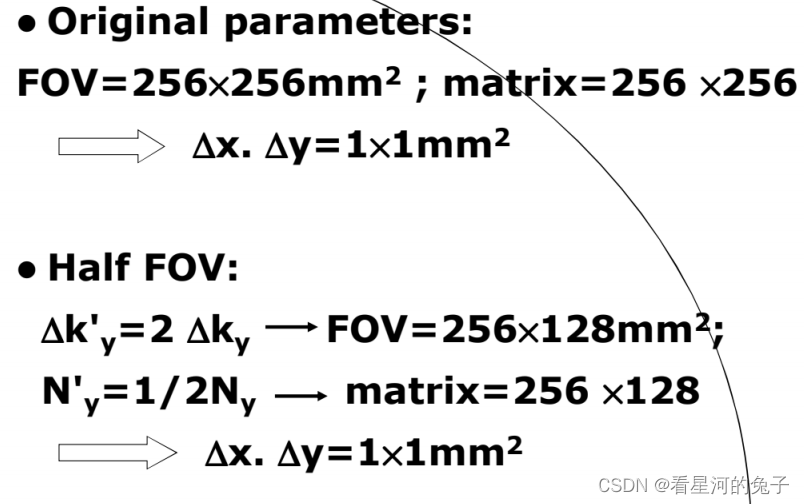
半 FOV 成像
- 提高速度,隔行填充数据,K 空间的单元尺寸增加⼀倍,FOV 图像减半,K 空间尺寸不变,所以图像空间
的像素大小不变
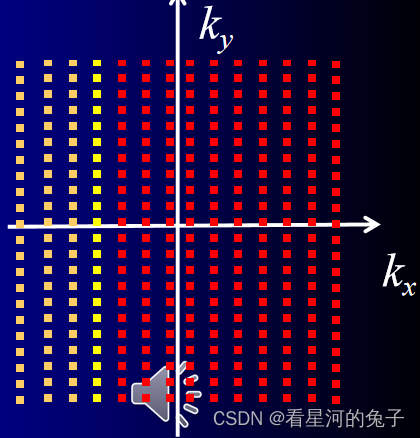
矩形矩阵扫描成像
- 提高速度,只填充靠近中央行的数据,K 空间的单元尺寸没有变化,FOV 图像不变,但 K 空间的空间尺寸
减半,所以图像空间的像素增加⼀倍

Ny代表只填了一半的数据,矩阵变小而FOV不变,则像素值变大
K空间与图像空间的关系
FOV
以x轴为方向讨论,不同方向的拉莫尔进动频率为:
f x = γ B x = γ G x x f_x=\gamma B_x=\gamma G_x x fx=γBx=γGxx
FOV 的中央列线上对应的磁场强度为 B0,左侧小于 B0,右侧大于 B0
则中央列上有最大频率
x = F O V x / 2 x=FOV_x/2 x=FOVx/2
f m a x = γ G x F O V x / 2 f_{max}=\gamma G_x FOV_x/2 fmax=γGxFOVx/2
则带宽BW
B W = γ G x F O V x BW=\gamma G_x FOV_x BW=γGxFOVx
最后可以得出FOV
F O V = B W / γ G FOV=BW/\gamma G FOV=BW/γG
则增加梯度场场强或降低带宽都可以减小FOV
且 B W = 1 / Δ T s BW=1/\Delta T_s BW=1/ΔTs
代入可得
1 F O V = γ G Δ T s \cfrac{1}{FOV}=\gamma G\Delta T_s FOV1=γGΔTs
同时考虑两个方向x和y
定义 Δ k x = γ G x Δ t x \Delta k_x=\gamma G_x\Delta t_x Δkx=γGxΔtx
最后:
则 Δ k x = γ G x Δ t x = 1 F O V x \Delta k_x=\gamma G_x\Delta t_x=\cfrac{1}{FOV_x} Δkx=γGxΔtx=FOVx1
Δ k y = γ G y Δ t y = 1 F O V y \Delta k_y=\gamma G_y\Delta t_y=\cfrac{1}{FOV_y} Δky=γGyΔty=FOVy1
k x = N x Δ k x , k y = N y Δ k y k_x=N_x\Delta k_x,k_y=N_y\Delta k_y kx=NxΔkx,ky=NyΔky
k x = 1 Δ x , k y = 1 Δ y k_x=\cfrac{1}{\Delta x},k_y=\cfrac{1}{\Delta y} kx=Δx1,ky=Δy1
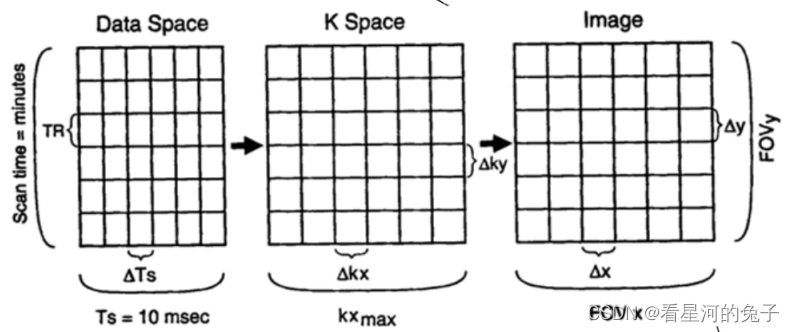
k空间单元尺寸与图像空间均成反比关系
这篇关于MRI k空间概念整理的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




